Библиографическое описание:
Кодиров, Ж. Р. Составление программного обеспечения, алгоритм и расчет математической модели применения свойств солнечного опреснителя к точкам заправки топливом / Ж. Р. Кодиров, Мусобек Маматрузиев. — Текст : непосредственный // Молодой ученый. — 2018. — № 26 (212). — С. 50-53. — URL: https://moluch.ru/archive/212/51885/ (дата обращения: 07.05.2024).
Для составления алгоритмов расчета используем блок-схемы алгоритмов. В чертеже- 1 приведена математическая модель алгоритма, составленного для сушилок.
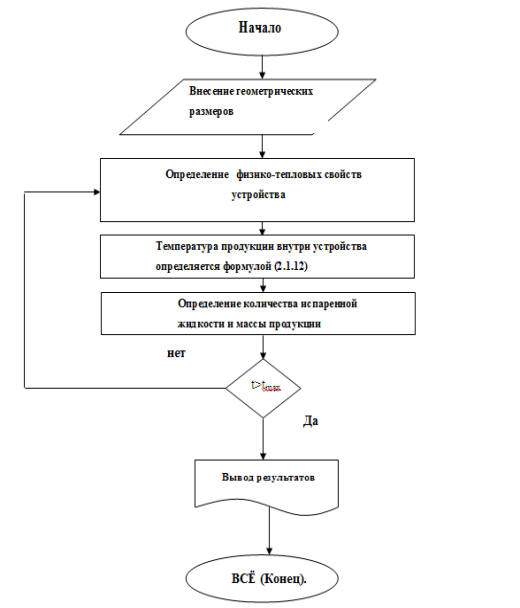
Рис. 1. Алгоритм в виде блок-схемы.
Рис. 2. Программа, составленная в профессиональной среде MathCAD 2001
Результаты расчетов иих анализы
и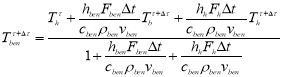 
Для решения этих уравнений, внешние параметры важны как предельные условия. Графический вид этих значений приведен на рисунках.
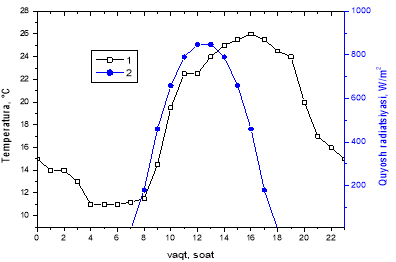
Рис. 3. Однодневное изменение внешней температуры (1) и солнечной радиации (2).
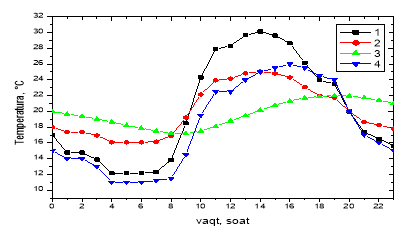
Рис. 4. Ёмкость для хранения жидкости (1), воздух внутри ёмкости (2), жидкость (3) и однодневное изменение внешней температуры (4).
На рис. 4. приведены значения однодневного изменения температур элементов цилиндрической ёмкости. Видно, что все температуры достигают своего максимального значения в течении 12–18 часов.
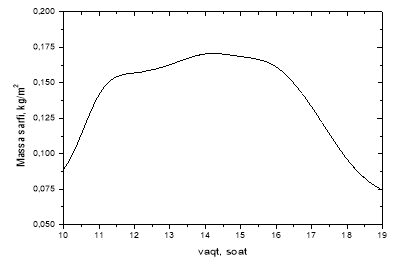
Рис. 5. Однодневное изменение расхода испаряемой массы жидкости
Расход массы взаимосвязан с разницей температур, и он тоже достигает своего максимального значения в течение 12–18 часов.
По итогам значений расчетов приведенных на рис. 5, когда внешние параметры, достигнут значений 1-го чертежа, количество жидкости, полученной конденсации в результате испарения, составит 4–5 литров в сутки.
Значения в трех графиках и их виды, могут быть разными, исходя из данных внешней температуры, из геометрических, физико-тепловых характеристик ёмкости. Для получения данных определенной географической широты, нужно использовать частные значения внешних параметров той местности.
Вывод:
-
Используя уравнение взаимосвязанности объема жидкости и высоты жидкости цилиндра, разработана программа, рассчитывающая связь объема жидкости с её высотой.
-
Для математической модели MathCAD 2001 создано программное обеспечение в профессиональной среде.
Основные термины (генерируются автоматически): внешняя температура, максимальное значение, однодневное изменение, профессиональная среда.
Похожие статьи
Рис. 5. Суточные изменения коэффициентов теплообмена, 1- коэффициент теплоотдачи с конвекцией между водой и прозрачной средой
Как видно из рис.3 максимальное значения температуры воды внутри установки достигает до 80°С и соответственно суточное значения...
Пользуясь указанными формулами, легко определить изменение температур в толще стены в любом
Максимальное значение упругости водяного пара соответствует максимальному
Соответственно температурам диффузия паров будет, происходит из сред с более высокими...
Всовременном обществе все большее значение приобретают осветительные приборы на
Все эти вопросы связаны со стратегией безопасности световой среды для человека.
Коррелированная цветовая температура светодиодного светильника (ТКЦ) равна 2900 К.
Внешними возмущающими воздействиями являются изменения наружной температуры, скорости ветра, солнечной радиации.
где = 53,36 т/ч; = 61,88 т/ч — расчётные расходы меньшей (греющей) и большей (нагреваемой) сред в отопительном подогревателе в точке...
При увеличении температуры окружающей среды уменьшение расхода воздуха, сжимаемого
Середа С. О., Гельмедов Ф. Ш., Сачкова Н. Г. Расчетные оценки изменения характеристик
- недопущение выхода за максимально допустимые значения температуры выхлопных газов и...
Повышенные значения температуры наружного воздуха в 2012 году оказали наиболее значительное влияние на потребление
Рис.3.Динамика изменения потребления электроэнергии в ОЭС Сибири 2012–2014гг. [1, 2, 3]. Из-за высокого промышленного статуса...
Температура наружной среды
1. Изменением температуры бетонной смеси с момента начала её укладки и до окончания процесса можно пренебречь
— максимальная глубина промерзания грунта, м; — глубина смерзания пучинистого грунта с поверхностью сваи, м: , где...
Это воздействие проявляется в изменении климата и солнечной активности, и возможно, в других внешних факторах.
Влияние окружающей среды может быть учтено в виде климатические показателей местности, в число которых входят: уровень осадков, температура...
Она зависит от скорости ветра, температуры окружающей среды и солнечного излучения.
Экспериментальный проект был реализован в целях проверки прогнозирования максимально-допустимых значений.
