Рассмотрены основные ошибки при построении CSG-моделей алгоритмом, работающим с полигональными объектами, а также предложены методы их решения.
Ключевые слова: компьютерная графика, пересечение многогранников, трёхмерная геометрия, Constructive Solid Geometry.
Введение.
Данная статья является дополнением к статье “Булевы операции на трёхмерных моделях в компьютерной графике” [1]. При реализации CSG-моделей алгоритмом, работающим с полигональными объектами [2], часто не учитываются частные случаи, которые создают ряд определённых сложностей при разработке программ, используемых для визуализации данных моделей.
Решение данной проблемы является важным для людей, работающих с компьютерной графикой, в частности, в области трёхмерного моделирования.
Алгоритмы построения CSG-моделей.
Существуют следующие алгоритмы построения CSG-моделей: работающие в пространстве изображения и работающие в пространстве объекта. Вторые являются более гибкими, к ним принадлежат алгоритмы, работающие с полигональными моделями, представляющие для нас интерес.
Алгоритм, работающий с полигональными объектами, обычно разбивают на три основных этапа [1]:
- нахождение линии пересечения двух заданных полигональных примитивов;
- разбиение каждого треугольника, которыми образован данный примитив, на группы треугольников, таким образом, чтобы каждый из отрезков являлся стороной двух смежных треугольников;
- решение задачи пространственной локализации треугольника одного примитива, относительно другого.
Ошибки впервом этапе.
Для поиска пересечения двух примитивов (рассматриваем треугольники) в пространстве удобно использовать алгоритм [3], однако, данный алгоритм не учитывает случаи, когда два примитива лежат в одной плоскости, притом, не параллельной ни одной из плоскостей проекции. Определить принадлежность двух треугольников одной плоскости достаточно просто при реализации алгоритма [3]: если расстояния
и 
(рис. 1).
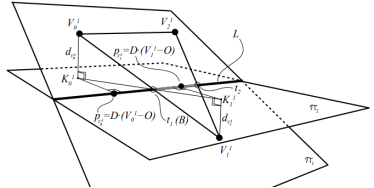
Рис. 1. Геометрическое представление алгоритма [3]
Решение. Если же два треугольника лежат в одной плоскости, то задача разбиения треугольников по линии пересечения будет решаться совершенно иначе. Два треугольника 
лежат в одной плоскости (рис. 2), тогда разбиение данных двух примитивов будет следующим (рис. 3).
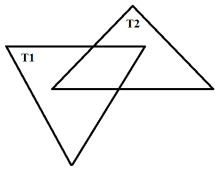
Рис. 2. Пересечение двух треугольников в одной плоскости
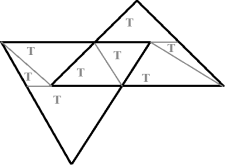
Рис. 3. Разбиение двух пересекающихся треугольников в одной плоскости на непересекающиеся примитивы
Ошибки во третьем этапе.
Самым удобным с точки зрения реализации и скорости выполнения является метод бросания лучей (ray-casting) [4]. Проблем с выбором точки испускания луча не возникает, однако возникает проблема с подсчётом количества пересечений выпущенного луча с примитивами второго объекта.
Рассмотрим основные случаи, которые могут возникнуть:
1) луч пересёк примитив, не через его сторону или же вершину;
2) луч пересёк примитив через его сторону;
3) луч пересёк примитив через его вершину.
Если в первом случае проблем не возникает, то два других случая заставляют задуматься, ведь, так как второй объект является замкнутым примитивом, то стороны всех его примитивов, а соответственно и вершин, соприкасаются как минимум с тремя другими. Именно поэтому возникает сложность в учёте истинного количества пересечений луча и примитивов другого объекта.
Решение в данном случае достаточно тривиальное: каждую вершину и сторону считать отдельным объектом и при пересечении учитывать только один раз.
Литература:
- Смелкова Е. А., Таразанов А. М., Меркулов Д. В., Иксарица Н. И., Погорелов Д. А., Булевы операции на трёхмерных моделях в компьютерной графике, Аллея Науки, Т. 1, № 1 (17), с. 860–864, 2018.
- R. Banerjee and J. Rossignac, Topologically exact evaluation of polyhedra defined in CSG with loose primitives, to appear in Computers Graphics Forum, Vol. 15, No. 4, pp. 205–217, 1996
- R. Banerjee and J. Rossignac, Topologically exact evaluation of polyhedra defined in CSG with loose primitives, to appear in Computers Graphics Forum, Vol. 15, No. 4, pp. 205–217, 1996
- ZAJÍČEK, Petr Acceleration of Ray-Casting for CSG scenes. Master thesis, MFF UK, 2012.
