Гидравлический расчет является одним из важных видов расчета при проектировании, эксплуатации, наладке и обследовании водяных тепловых сетей. При его выполнении решается ряд задач, а именно:
- Вычисление диаметров трубопровода.
- Вычисление потерь напора (давления) как на отдельных участках тепловой сети, так и в сумме по всей длине магистрали или сложного ответвления.
- Вычисление напора (давления) в разных точках тепловой сети.
- Увязка ответвлений с магистралью для обеспечения правильного распределения расхода теплоносителя и требуемых напоров в сети и у потребителей.
- Определение пропускной способности сети при известных диаметрах и заданном падении напора.
И, как следствие, от его правильного выполнения зависят: денежные затраты при строительстве и эксплуатации теплосетей, выбор оптимального оборудования, рекомендации по наладке и оптимизации работы существующих тепловых сетей.
На сегодняшний день большинство методик гидравлического расчета трубопроводов основывается на уравнении Дарси-Вейсбаха [1]. Согласно ему, потери давления в трубопроводе равны, Па:
![]() (1)
(1)
где λ — безразмерная величина, называемая коэффициентом гидравлического трения; L — расчетная длина трубопровода, м; ρ — плотность теплоносителя, кг/м3; w — средняя скорость течения теплоносителя, м/с; d — расчетный диаметр трубопровода, м.
В инженерной практике формула (1) часто используется в следующем виде, Па:
![]() (2)
(2)
где R — удельные потери давления на трение, которые определяются по формуле, Па/м:
![]() (3)
(3)
В формуле (3) наибольшую трудность представляет задача по определению значения коэффициента гидравлического трения λ, так как данная величина в общем случае зависит от режима течения жидкости и свойств материала трубопровода. Теплосети работают в области турбулентного режима, для которого предложено множество формул по расчету коэффициента гидравлического трения. Наиболее простой для применения в практических расчетах является универсальная формула Альтшуля:
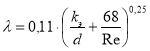 (4)
(4)
где kэ — коэффициент эквивалентной шероховатости, м; Re — безразмерная величина, называемая критерием Рейнольдса, которая характеризует режим течения жидкости и определяется по формуле:
![]() (5)
(5)
где ν — кинематическая вязкость, м2/с.
Поэтому, с учетом формулы (4), зависимость (3) можно записать в следующем виде, Па/м:
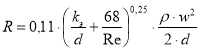 (6)
(6)
В литературе [2] формула удельных потерь давления, с учетом предположения о том, что большинство тепловых сетей работают в области квадратичного режима и принимая плотность теплоносителя постоянной, принимает следующий вид, Па/м:
![]() (7)
(7)
где G — массовый расход теплоносителя, кг/с.
В то же время в работе [3] на основе обобщения и упрощения известных данных и зависимостей приведена следующая формула, Па/м:
![]() (8)
(8)
где A, a, b — эмпирические коэффициенты, зависящие от материала трубопровода и его назначения; d — расчетный диаметр трубопровода, мм.
Формулы (6) — (8) для определения удельных потерь давления на трение используются при гидравлическом расчете тепловых сетей, но все они могут давать различные между собой результаты. Поэтому необходимо провести сравнение результатов гидравлического расчета по этим зависимостям.
Для этого была выбрана тепловая сеть, расположенная на территории г. Владимира, спроектированная из стальных труб (kэ =0.0005 м) на температурный график 150/70 ° С. Исходные данные для расчета по участкам теплосети приведены в таблице 1.
Таблица 1
Исходные данные для расчета
|
№уч. |
Длина участка L, м |
Расход воды на участке G, кг/с |
Внутр. диаметр dу, м |
Наруж. диаметр dн, м |
Скорость воды w, м/с |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
И-1 |
22,1 |
55,7 |
0,25 |
0,273 |
1,18 |
|
1–2 |
415,6 |
53,7 |
0,25 |
0,273 |
1,14 |
|
2–3 |
167,6 |
27,1 |
0,2 |
0,219 |
0,9 |
|
3–4 |
66,4 |
26,3 |
0,2 |
0,219 |
0,87 |
|
4–5 |
63 |
24,4 |
0,175 |
0,194 |
1,06 |
|
5–6 |
61,4 |
22,5 |
0,175 |
0,133 |
0,98 |
|
6–7 |
65,7 |
10,1 |
0,125 |
0,133 |
0,86 |
|
7–8 |
123,8 |
7,7 |
0,125 |
0,108 |
0,65 |
|
8–9 |
212,1 |
1,96 |
0,07 |
0,076 |
0,53 |
В водяных тепловых сетях обычно вместо потерь давления оперируют величиной потерь напора, которая вычисляются по формуле м:
![]() (9)
(9)
где g — ускорение свободного падения, равное 9,81 м/с2.
Для удобства расчета каждому из расчетов были присвоены следующие номера:
I — расчет удельных потерь давления и потерь напора с использованием формулы (6);
II — расчет удельных потерь давления и потерь напора с использованием формулы (7);
III- расчет удельных потерь давления и потерь напора с использованием формулы (8).
В таблице 2 приведены результаты расчета удельных потерь давления и потерь напора по каждому участку. В формуле (7) значение коэффициента ABR = 13,62 · 10 -6 м3,25/кг при kэ равным 0.0005 м. В формуле (8) для водяных тепловых сетей А=6,01; а = 1,9; b= 1,3.
Таблица 2
Результаты расчета удельных потерь давления ипотерь напора по участкам
|
№уч. |
I |
II |
III | |||
|
R, Па/м |
ΔН, м |
R, Па/м |
ΔН, м |
R, Па/м |
ΔН, м | |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
И-1 |
63,48 |
0,15 |
64,17 |
0,15 |
61,24 |
0,15 |
|
1–2 |
59,03 |
2,63 |
59,87 |
2,67 |
56,93 |
2,54 |
|
2–3 |
48,57 |
0,87 |
50,91 |
0,91 |
46,74 |
0,84 |
|
3–4 |
45,75 |
0,33 |
48,09 |
0,34 |
44,02 |
0,31 |
|
4–5 |
79,22 |
0,53 |
82,37 |
0,56 |
76,35 |
0,52 |
|
5–6 |
67,38 |
0,44 |
70,59 |
0,46 |
64,9 |
0,43 |
|
6–7 |
80,42 |
0,57 |
86,63 |
0,61 |
77,37 |
0,54 |
|
7–8 |
46,02 |
0,61 |
50,82 |
0,67 |
44,12 |
0,59 |
|
8–9 |
63,13 |
1,44 |
73,03 |
1,66 |
60,35 |
1,36 |
Как видно из таблицы 2, результаты расчетов отличаются друг от друга. Для дальнейшего анализа необходимо вычислить относительную погрешность расчета потерь напора, которая определяется по формуле, %:
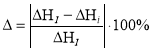 (10)
(10)
где i — номер расчета, ΔН — потери напора, м.
За точные результаты примем значения, полученные в расчете I, так как зависимость для определения коэффициента гидравлического трения, входящая в нее, используется в большинстве практических расчетов и дает результаты, которые хорошо соотносятся с опытными данными различных исследователей.
В таблице 3 представлены расчеты погрешности относительно расчета I как по каждому участку, так и по суммарным потерям напора на всей магистрали в целом.
Таблица 3
Расчет относительной погрешности удельных потерь давления ипотерь напора
|
№уч. |
I |
II |
III | ||
|
ΔН, м |
ΔН, м |
Δ,% |
ΔН, м |
Δ,% | |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
И-1 |
0,15 |
0,15 |
1,09 |
0,15 |
3,53 |
|
1–2 |
2,63 |
2,67 |
1,43 |
2,54 |
3,56 |
|
2–3 |
0,87 |
0,91 |
4,82 |
0,84 |
3,76 |
|
3–4 |
0,33 |
0,34 |
5,1 |
0,31 |
3,79 |
|
4–5 |
0,53 |
0,56 |
3,98 |
0,52 |
3,62 |
|
5–6 |
0,44 |
0,46 |
4,75 |
0,43 |
3,69 |
|
6–7 |
0,57 |
0,61 |
7,72 |
0,54 |
3,8 |
|
7–8 |
0,61 |
0,67 |
10,42 |
0,59 |
4,12 |
|
8–9 |
1,44 |
1,66 |
15,68 |
1,36 |
5,24 |
|
И-9 |
7,57 |
8,04 |
6,25 |
7,27 |
3,99 |
Как видно из таблицы 3, относительная ошибка по суммарным потерям на магистрали не превышает 4 % для расчета по формуле (8) и не превышает 7 % по формуле (9), что для инженерной практики можно считать весьма удовлетворительным. Однако стоит заметить, что в результате расчета по формуле (9), относительная ошибка на отдельных участках выше 15 %, что накладывает ограничения на применение данной формулы. Например, при увязке ответвлений, относительная ошибка между ответвлением и рассматриваемой частью магистрали не должна превышать 15 %.
В заключение хотелось бы отметить, что существует множество расчетных зависимостей по определению потерь давления (напора) в трубопроводах, но все они так или иначе применимы для определенных случаев с учетом ряда допущений. Применяя даже упрощенные варианты известных зависимостей, приходится выполнять расчеты по каждому из участков тепловой сети, что делает расчет весьма трудоемким, особенно при конфигурации сети с большим количеством участков и ответвлений. Все это создает предпосылки для дальнейшего совершенствования подходов гидравлического расчета.
Литература:
- Гидравлика и гидропривод: Учебное пособие /Н. С. Гудилин, Е. М. Кривенко, В. С. Маховиков и др. — М.: Изд-во МГГУ, 2001. — 520 с.
- Соколов Е. Я. Теплофикация и тепловые сети: учебник для вузов. — 7-е изд., стереотип. — М.: Изд-во МЭИ, 2001. — 472 с.
- Самарин О. Д. Построение универсальной зависимости для потерь давления в трубопроводах// Журнал С. О. К., № 1/2016.

