Внаучной статье приведен анализ для расчёта устойчивости управления с помощью критериев электрорезонансного контура с линейно-индуктивными элементами через диодный мост, применяемый в обмотке управления магнитного усилителя. Для исследования электрорезонансного контура аппроксимируем кривую намагничивания степенной функцией, вводя безразмерные и базисные величины и используя метод медленно меняющихся амплитуд, что отвечает решению устойчивости, полученному базовыми уравнениями в обмотке управления.
Ключевые слова: системы управления, напряжения сетипеременного тока, электрорезонансного контура с линейно-индуктивными элементами, аппроксимирующей функции, метод медленно меняющихся амплитуд, базисные и безразмерные коэффициенты, критерий устойчивости.
Исследование условий устойчивости системы управления принципиально может быть выполнено путем определения знака корней характеристического уравнения, соответствующего дифференциальному уравнению в системе цепи управления. Системы управления разделяются на основные элементы и звенья. Составляются уравнения переходного процесса для каждого звена. При этом рассматривают явления при отклонениях регулируемой величины, что дает возможность упростить задачу и рассматривать переходные процессы в звеньях протекающей по линейному закону.
Через систему дифференциальных уравнений звеньев, можно найти линейное дифференциальное уравнение. Составление уравнения определяет связь между величинами на входе и выходе системы регулирования в целом. Необходимо определить знаки у всех вещественных корней и у всех вещественных частей сопряжено-комплексных корней рассматриваемого характеристического уравнения.
Система управления будет устойчивой, если все вещественные корни и вещественные части сопряжено-комплексных корней будут отрицательными. Если же вещественные корни и вещественные части сопряжено-комплексных корней будут положительными, то это значит, что система регулирования неустойчива.
Задача об определении условий устойчивости линейных систем регулирования, не прибегая к решению характеристического уравнения, впервые была поставлена еще в 1868 г. Максвеллом. В 1876 г. И. А. Вышнеградским был предложен критерий устойчивости применительно к системам критериев устойчивости и их обобщениям, этой проблеме были посвящены работы Рауса, Гурвица, Найквиста, Михайлова, Соколова, Неймарка и другие.
В настоящее время наиболее распространенные критерии устойчивости могут быть разделены на две основные группы:
а) алгебраическиекритерии, основанные на изучении знаков коэффициентов характеристического уравнения и знаков комбинаций из этих коэффициентов. Он относятся, широко известный критерий Рауса-Гурвица;
б) частотные критерии, основанные на изучении расположения некоторых частотных характеристик в комплексной плоскости.
Частотный критерий А. В. Михайлова, применяемый для изучения сложных многоконтурных систем, рассматриваемых при этом в виде замкнутых систем регулирования, и критерий Найквиста-Михайлова, применяемый для простых одноконтурных систем, рассматриваемых в целях упрощения анализа в виде разомкнутых систем регулирования.
Для расчёта устойчивости систем автоматического управления применяется следующие критерий устойчивости:
– критерий устойчивости Рауса-Гурвица;
– критерий устойчивости А. В. Михайлова;
– критерий устойчивости Найквиста- Михайлова.
Особенностью всех частотных критериев, применение которых сопровождается графическими построениями на комплексной плоскости, является их наглядность. Всех критериев устойчивости управления, в том числе частотных является то, что с их помощью можно решить только один вопрос: устойчива система управления или неустойчива. Критерий устойчивости Рауса-Гурвица. В 1877г. Рауса метод исследования условий устойчивости в форме правила, определяющего последовательность операций, необходимых для решения задачи. Эти правила могут быть названы условием Рауса, которое применительно к линейным системам может быть сформулировано следующим образом:
– система управления, описываемая линейным дифференциальным уравнением с постоянными коэффициентами, будет устойчивой;
– если все коэффициенты характеристического уравнения будут положительными.
В 1895г. Гурвица показал, что условие устойчивости Рауса только для тех частных случаев, когда все корни характеристического уравнения вещественные. Когда корни характеристического уравнения могут быть как вещественные, так и сопряжено-комплексными, условие устойчивости Рауса является необходимыми, так как оно не охватывает условия отрицательности вещественной части комплексных корней.
Гурвиц показал, что система регулирования будет устойчивой, если все коэффициенты a0, a1, a2, ……, an характеристического уравнения вида
a0 pn+ a1 pn-1+ a2pn-2+........+an-1p+an=0 (1)
положительный и если составленный по определенному закону определитель порядка n-1,а также все его главные миноры также положительны.
По главной диагонали, (1) слева направо, вниз выписываются последовательно все коэффициенты характеристического уравнения, исключая первый и последний коэффициенты a0 и an.
Система управления описывается линейным дифференциальным уравнением третьего порядка с постоянными коэффициентами. Характеристическое уравнение имеет вид:
![]()
Аналогично составляются и вычисляются условия для критерия устойчивости Рауса-Гурвица и для систем регулирования, имеющих характеристическое уравнение более высокого порядка [3].
Нами дано статье для анализа устойчивости применив материалов существующих критериев электромагнитно резонансного контура с линейно-индуктивным элементом, применяемого в обмотке управления магнитного усилителя [1,4]. В дальнейшем это даёт возможность для математического анализа режим устойчивости электрическими цепью электромагнитно резонансных контуров с линейно-индуктивными элементами создаваемого стабилизаторов тока и напряжения на базе магнитного усилителя. Теоретически анализировано электрические цепи при синусоидальном напряжении сети электромагнитного контура (рис.1), так и вынужденные колебания. Вольтамперной характеристикой цепи можно обусловить появление области многозначных решений [4, 5]. Поэтому необходимо рассмотреть вопросы устойчивости цепи.
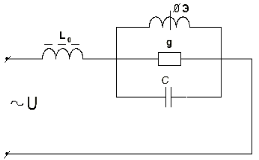
Рис. 1. Схема соединения электромагнитно резонансного контура.
Для рассматриваемой цепи в следующее соотношение:
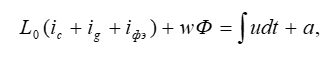 (2)
(2)
Учитывая, ![]()
![]()
![]()
Вводя замену переменных
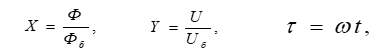 (3)
(3)
и подставляя (3) в (2) получим
![]()
Учитывая базисные величины и принимая
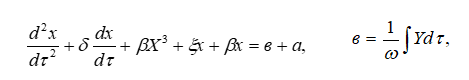 (4)
(4)
Уравнение (4) решим методом медленно меняющихся амплитуд.
Пусть
![]()
После некоторых математических преобразований имеем:
![]() (5)
(5)
По критерию Гурвица система устойчива,
![]()
Первое условие
![]() не ограничивает устойчивость.
не ограничивает устойчивость.
![]() из (5) имеем следующее условие:
из (5) имеем следующее условие:
![]() (6)
(6)
Первая составляющая всегда больше нуля, поэтому исследуем вторую составляющую. При
![]()
Тогда имеем следующее условие
Таким образом, можно заключить, что решение, отвечающие устойчивому состоянию цепи электрорезонансного контура с линейно-индуктивным элементом, применяемого в обмотке управления магнитного усилителя [4, 5], существенно зависит от соотношения параметров L0, электромагнитного элемента и C.
Выводы
- Приведение критерий устойчивости для состояния магнитно резонансного контура с линейно-индуктивным элементом к базисным условиям позволяет получить дифференциальное уравнение с минимальным количеством коэффициентов. Можно теоретически анализировать устойчивости резонансного контура с линейно-индуктивным элементом применяемого в обмотки управления магнитного усилителя.
- Применение критериев устойчивости для математического анализа устойчивости нелинейной цепи даёт намеренной результаты.
Литература:
- Кадыров Т. М. Анализ установившихся режимов ЭФМ цепей с падающими амплитудными характеристиками. Узбексий журнал Проблемы информатики и энергетики. -Ташкент.: 1993. № 5. -33–37с.
- Веников В. А., Литкенс И. В. Математические основы теории автоматического управления режимами электросистем. — М.: «Высшая школа», 1964.
- Гизила Е. П. Расчёт устройств автоматики энергосистем. — Киев.: Издательства «Технiка», 1969. -264с.
- Файзиев М. М., Тошев Т. У., Орипов А. А. Активно-индуктивная нагрузка стабилизатора на базе магнитного усилителя. Федеральный журнал «Наука, техника и образование» -М.: Россия, № 3 (21) март 2016. -108–111с.
- Файзиев М. М., Тошев Т. У., Ниматов К. Б., Умиров А. П. Обобщенные характеристики магнитного усилителя. Федеральный журнал «Наука, техника и образование» -Москва.: Россия, № 4 (22) апрель 2016. -24–27с.







