При решении военно-прикладной задачи первым этапом является построение математической модели, которое часто осуществляется при помощи обыкновенных дифференциальных уравнений. Эти уравнения, связывающие независимую переменную, искомую функцию и её производные, являются основой многих законов материального мира. С их помощью можно установить связь между кривой и её касательной, пройденным путём и скоростью движения, описать такие известные физические законы как второй закон Ньютона и закон Гука.
Часто сам процесс вывода дифференциального уравнения представляет собой сложную математическую задачу. Во-первых, для построения модели, адекватной рассматриваемому явлению или процессу, необходимы глубокие знания в смежных областях науки, таких как физика, теоретическая механика и динамика полёта. Во-вторых, получающееся в процессе построения математической модели дифференциальное уравнение должно по возможности приводиться к уравнению известного вида: линейного, однородного и т. п. Поэтому часто бывает необходимо ввести различные упрощения, но при этом учесть все основные факторы, влияющие на процесс.
Рассмотрим некоторые задачи военно-прикладного характера, основанные на решении дифференциальных уравнений первого порядка.
Пример 1.
В некоторый момент времени самолёт-цель находится в точке А, истребитель в районе точки В. Скорости цели и истребителя соответственно равны 
и 
(
). Установить траекторию полёта истребителя в горизонтальной плоскости от точки В, чтобы обнаружить цель, если от точки А цель летит прямолинейно, но с неизвестным курсом.
Решение. Пусть цель летит из точки А в точку В, то время полёта будет равно 
, где 
расстояние от точки A до точки B. За это время истребитель должен прибыть в точку В. Если в точке В цель не будет обнаружена, т. е. она следует не по прямой АВ, истребитель следует из точки В по какой-то кривой. Пусть точка М, принадлежащая этой кривой, является точкой предполагаемой встречи. Пути, проходимые целью и истребителем, найдём по формулам:
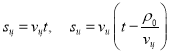. Выражая 
из первой формулы и подставляя во вторую, получим 
. Пусть точка М имеет полярные координаты 
в системе координат с началом координат в точке A. Тогда
. Дифференцируя по 
, найдем 
. Используя формулу 
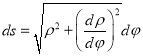, получим равенство 
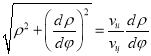. После несложных преобразований перейдём к дифференциальному уравнению 
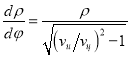. Приняв 
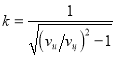, будем иметь 
. Решением уравнения с разделяющимися переменными 
будет семейство функций 
или 
. Учитывая начальные условия 
, найдём 
, тогда 
. Получили уравнение логарифмической спирали, по которой должен лететь истребитель, чтобы обнаружить цель.
Пример 2.
Истребитель пикирует с горизонтального полёта. Определить закон изменения скорости пикирования по вертикальной составляющей в зависимости от пути, пройденного истребителем. Сопротивление воздуха считать пропорциональным квадрату скорости.
Решение. На самолёт при пикировании действует сила тяжести 
и сопротивления воздуха 
, где 
это пройденный самолётом путь по вертикали за время 
. На основании второго закона Ньютона получим дифференциальное уравнение 
. Так как в задаче требуется установить связь между скоростью 
и пройденным по вертикали путём 
, то введём переменную 
. Тогда 
. Отсюда получим 
или 
, откуда 
. Значение 
найдём с учётом начальных условий: при 
откуда 
Подставив 
в общее решение, найдём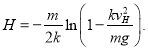 
Получили закон изменения скорости пикирования по вертикальной составляющей в зависимости от пути, пройденного самолётом.
Пример 3.
На высоте 2 км самолёт начинает боевой разворот и выполняет его с постоянной скоростью 
км/ч и углом наклона траектории к горизонту 
. За сколько времени самолёт достигнет высоты 3 км? На какую высоту поднимется самолёт за 30 секунд?
Решение. Пусть 
высота, на которой находится самолёт. Из условия получим, что 
. Тогда 
, откуда 
Учитывая, что 
, из последней формулы получим, что время, за которое самолёт достигнет высоты 3 км равно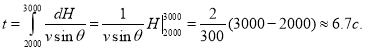 
Аналогично получаем, что 
, откуда высота, на которую самолёт поднимется за 30 секунд можно найти как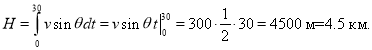 
Литература:
- Филиппов А. Ф. Сборник задач по дифференциальным уравнениям.– Ижевск: НИЦ «Регулярная и хаотическая динамика», 2000. –176с.
- Докучаев В. Д., Озерецковская М. М. Высшая математика. Военно-прикладные задачи.– Тип. СВВАУЛШ, 1989.– 127c.
