Современная теория графов позволяет создавать удобные методы для моделирования разнообразных систем, состоящих из отношений объектов различной природы, поэтому она находит своё применение не только в математике, но и в ее приложениях в самых разных областях науки и техники. Одной из важных задач теории графов является задача раскраски вершин графа.
Пусть
— некоторый произвольный граф, множество 
будем называть красками. Раскраской (t-раскраской) графа G называется отображение 
из V в такое, что для двух любых вершин u и v этого графа выполняется условие 
То есть t-раскраска графа приписывает каждой его вершине один из цветов так, что две любые смежные вершины имеют разные цвета.
Если G — неориентированный граф без петель и кратных рёбер, то P(G,x) — хроматическая функция (хроматический полином), которая принимает значение для любого целого неотрицательно числа из заданного множества красок, равное числу x-раскрасок графа.
Очевидна справедливость следующих утверждений.
Утверждение 1. Хроматический полином нулевого графа с n вершинами равен 
, так как все вершины нулевого графа 
можно раскрасить в любой из x заданных цветов.
Утверждение 2. Хроматический полином полного графа 
равен 
, так как первую вершину можно окрасить в любой из имеющихся цветов, вторую вершину можно окрасить в любой из оставшихся цветов, и т. д.
Следующее утверждение позволяет раскраску любого графа свести к раскраске некоторого числа полных графов.
Утверждение 3. Пусть G — обыкновенный граф. Обозначим G1 граф, полученный добавлением в G ребра, соединяющего две несмежные вершины, а G2 — граф, полученный стягиванием этого ребра, тогда
Очевидно, что с помощью утверждения 3 для любого обыкновенного графа G c n вершинами полином 
можно представить в виде суммы хроматических полиномов полных графов
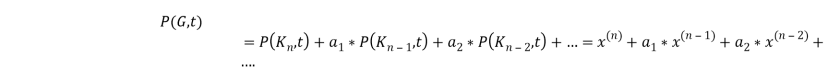
Очевидно, что старший коэффициент данного полинома равен 1, а степень многочлена равна n. Нахождение семейства полных графов путём использования утверждения 3 называется хроматической редукцией графа G.
Утверждение 4. На основе утверждения 3 можно использовать следующую формулу
Очевидно, что с помощью данного утверждения удобно вычислить хроматический многочлен графа по степеням переменной x в тех случаях, когда количество рёбер в графе меньше половины количества рёбер полного графа.
Для того чтобы приступить к конструированию алгоритма вычисления хроматического полинома, необходимо определиться со способом задания графа. Существует несколько способов задания графа: графический, матрицей смежности, матрицей инцидентности, множеством вершин и рёбер и другие. Для удобства будем использовать способ задания графа путём перечисления двух множеств: множества вершин и множества рёбер. Стоит обратить внимание, что название ребра составляется из названия двух инцидентных ему вершин. В случае, когда в графе нет вершин степени ноль, нет необходимости в создании множества вершин, так как все вершины являются инцидентными какому-нибудь ребру.
Для описания графа создан класс public class Graph. Класс представляет собой конструкцию, позволяющую создавать собственные настраиваемые типы при помощи группирования переменных других типов, методов и событий. Если класс не объявлен статическим, то клиентский код может создавать его экземпляры. Экземпляр класса остается в памяти до тех пор, пока все ссылки на него не выйдут из области.
Внутри класса создаются поля. Поле — это переменная, являющаяся членом класса или структуры. Инициализация поля не обязательна. Ради удобства объявляется несколько полей одного типа. Внутри класса создаются методы. Метод выполняет определённое действие с помощью последовательности операторов. Метод может принимать входные данные от вызвавшего кода через параметры. Кроме того, он может отправлять данные вызвавшему коду в соответствии с типом возвращающего значения. Если в качестве типа возвращаемого значения указан void, то метод не возвращает никакого значения. Метод также может отправлять данные вызвавшему коду с помощью параметров, имеющих модификатор ref или out.
Сигнатура метода должна быть уникальна в пределах типа. Она включает в себя имя метода и типы его параметров (но не имена параметров и не тип возвращаемого значения). Далее создаются конструкторы. Конструкторы выполняют код инициализации для класса или структуры.
Конструктор определяется, как метод, с тем отличием, что имя метода и тип возвращаемого значения сводится к имени типа, содержащего конструктор. Для классов компилятор C# автоматически генерирует конструктор без параметров тогда и только тогда, когда не определены никакие конструкторы. Если же определить хотя бы один конструктор, конструктор без параметров больше генерироваться не будет. Для структур конструктор без параметров является неотъемлемой частью, поэтому вы не можете определить свой собственный. Роль неявного конструктора без параметров у структуры состоит в том, чтобы инициализировать все поля значениями по умолчанию.
Для конструирования хроматического полинома были созданы следующие классы:
1) public class ChromoKey — служебный класс, описывающий множество полных графов, найденных при разложении, а также количество каждого из них;
2) public partial class Edge — класс, описывающий ребра, причём данный класс использует вершины, так как ребром в данной задаче является пара смежных вершин;
3) public partial class Vertex — класс, описывающий вершины;
4) public class Graph — класс, описывающий граф. Данный класс содержит условия, при которых граф является простым циклом или деревом. Класс имеет следующие методы: добавление и удаление множества рёбер, добавление и удаление множества вершин, добавление ребра (и новых вершин, если такие есть), удаление ребра (вершины остаются), добавление вершины, удаление вершины (удаляются и все рёбра, в которых встречается указанная вершина), две вершины инцидентны, все возможные рёбра на вершинах данного графа, множество рёбер дополнения графа, граф полный (если дополнение пустое), конструктор графа по множеству рёбер, конструктор графа по множеству вершин, конструктор графа по множеству вершин и рёбер, степень вершины;
5) public static class GraphAlGorithms — статический класс, содержащий алгоритм нахождения хроматического полинома;
6) public class Polynome — класс, описывающий полином. Данный класс содержит следующие методы: конструктор, индексатор для доступа к коэффициентам, копирование полинома, оператор перемножения двух полиномов, оператор умножения полинома на целое число справа, оператор умножения полинома на целое число слева, оператор сложения двух полиномов, преобразование полинома в строку.
Индексаторы обеспечивают естественный синтаксис для обращения к элементам класса или структуры, которые инкапсулируют список или словарь значений. Индексаторы аналогичны свойствам, но обращение к ним происходит не по имени, а с помощью индексного аргумента. Класс string имеет индексатор, позволяющий обратиться к любому символу, указав целочисленный индекс. В одном типе можно объявить несколько индексаторов.
Статический конструктор выполняется один раз для типа, а не каждый раз для нового экземпляра. Он выполняется до создания каких-либо экземпляров этого типа и до обращения к любым другим статическим членам. В типе может быть определен только один статический конструктор. Он должен быть без параметров, а его имя должно совпадать с именем типа. Присвоение значений статическим полям происходит до вызова статического конструктора, в порядке их объявления.
Статический конструктор всегда вызывается косвенно, на этапе выполнения; он не может быть вызван явно. Среда выполнения гарантирует, что статический конструктор типа будет вызван в некоторый момент до использования этого типа, однако, невозможно сказать, когда именно. Если класс статический, то он состоит исключительно из статических членов, и от него нельзя произвести подкласс.
Класс может наследовать от другого класса, то есть расширять или изменять возможности последнего. Наследование позволяет повторно использовать функциональность класса, не создавая новый код. Класс может наследовать только от одного класса, но от него самого могут наследовать несколько классов, в результате чего возникает иерархия классов.
Для построения хроматического полинома графа воспользуемся утверждением 3. Для этого создадим статический класс public static class GraphAlGorithms. Данный класс будет содержать рекурсивное решение задачи поиска хроматического полинома для заданного графа.
Далее в этом классе необходимо создать процедуру добавления ребра в граф.
public static Graph MerGeGraph(Graph G, EdGe e)
{ var merGedGraph = new Graph(G.EdGes);
merGedGraph.Add(e);
return merGedGraph; }
Также необходима процедура стягивания двух вершин графа.
public static Graph ContractGraph(Graph G, EdGe e)
{ var contractedGraph = new Graph(G.EdGes);
var u = e.Vertices.First(); // остающаяся вершина
var v = e.Vertices.Last(); // удаляемая вершина
var vertices = G.EdGes.Where(_ => _.Vertices.Contains(v)).SelectMany(_ => _.Vertices);
foreach (var vertex in vertices) contractedGraph.Add(new EdGe(vertex, u));
contractedGraph.Remove(v);
return contractedGraph; }
Теперь приступим к конструированию алгоритма. На первом шаге обратимся к классу ChromoKey и создадим новый пустой объект класса, так как на первом этапе еще не найдено не одного полного граф в разложении.
var result = new ChromoKey();
Следующим шагом определим условие, при котором заданный граф с n вершинами оказался полным, в таком случае в возвращаемом значении будет содержаться информация, что граф вида найден 1 раз.
if (Graph.IsComplete)
{ result.WeiGhts [Graph.Vertices.Count()] = 1;
return result; }
Если предыдущее условие не выполнено, то переходим к процессу создания двух новых графов. Первый граф создаётся путём добавления к исходному графу первого ребра из его дополнения (этого ребра нет в исходном графе).
var edGe = Graph.ComplementEdGes.First();
var merGedGraph = MerGeGraph(Graph, edGe);
Затем создаём граф, полученный стягиванием первого ребра из дополнения.
var contractedGraph = ContractGraph(Graph, edGe);
И далее создаём рекурсивное добавление результатов для полученных двух графов.
result += ChromaticPolynomRecursive(merGedGraph) + ChromaticPolynomRecursive(contractedGraph);
В итоге мы получаем сконструированный алгоритм для нахождения хроматического полинома заданного неориентированного графа.
Приведём некоторые примеры нахождения хроматического полинома различных графов.
Пример 1. Рассмотрим граф 
. Для него хроматический полином имеет вид: 
. Результат работы программы для графа приведён на рисунке 1.
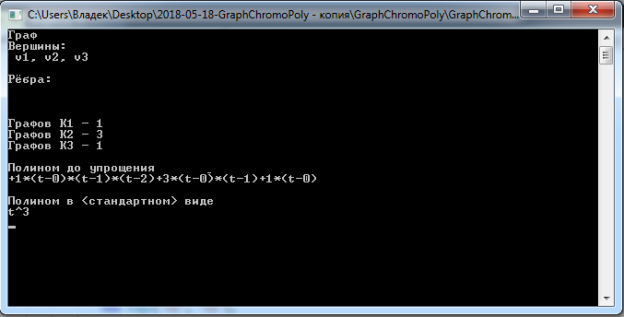
Рис. 1. Результат работы программы для пустого графа
Пример 2. Рассмотрим граф 
. Для него хроматический полином имеет вид: 
. Результат работы программы для графа приведён на рисунке 2.
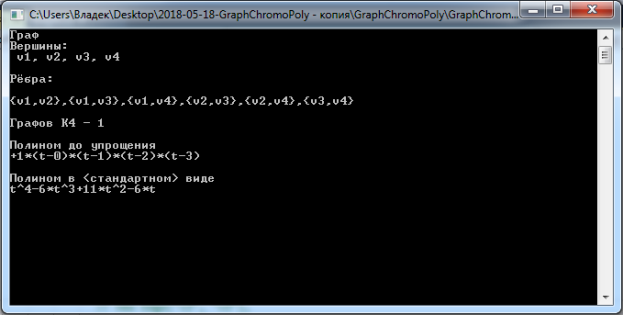
Рис. 2. Результат работы программы для полного графа
Пример 3. Рассмотрим некоторый граф с рёбрами {(1–2), (2–3), (3–4), (3–5), (5–6), (4–6), (1–6)}. Его хроматический полином имеет вид: 
. Результат работы программы для данного графа приведён на рисунке 3.
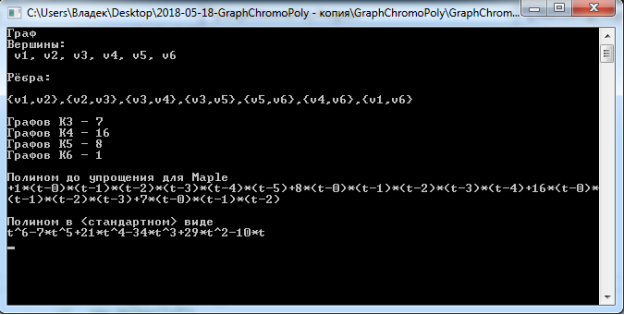
Рис. 3. Результат работы программы для неориентированного графа
Данный алгоритм реализован на объектно-ориентированном языке программирования С# в среде разработки Microsoft Visual Studio.
Литература:
- Асанов М. О., Баранский В. А., Расин. В. В. Дискретная математика. Графы, матроиды, алгоритмы. Лань, 2010
- Мальцев Ю. Н., Петров Е. П. Введение в дискретную математику. Элементы комбинаторики, теории графов и теории кодирования. Издательство алтайского государственного университета, 1997
- Прайс Д. Visual C# 2.0. Полное руководство, 2010
- Сухан И. В., Иванисова О. В., Кравченко Г. Г. Графы: учебное пособие. Кубанский государственный университет, 2015
