Данная статья посвящена вопросам применения математического программного обеспечения Mathcad для визуализации и интуитивного понимания странных аттракторов. Рассмотрев вкратце теорию и историю изучения фракталов и аттракторов, авторы останавливаются на их исследовании и моделировании на примере странного аттрактора Лоренса при вводных данных σ, b, r, y.
Вопрос понимания странных аттракторов являлся достаточно сложным, однако после появления современных вычислительных программных обеспечений вопрос создания визуализированного изображения был решён.
Аттра́ктор от англ. attract — привлекать, притягивать — множества, к которым приближаются точки при последовательных итерациях отображения. Притягивающая неподвижная точка (например, в задаче о маятнике с трением) и периодическая траектория (пример — самовозбуждающиеся колебания в контуре с положительной обратной связью) являются простейшими вариантами аттрактора, однако бывают и гораздо более сложные примеры.
Когда динамика параметров является хаотичной, то фрактал имеет фрактальную структуру и называется странным. Флорисом Такенсом и Дэвидом Рюэлем впервые ввели это определение. Объектом их исследования был аттрактор, возникший в результате неоднократных бифуркаций системы потока жидкости. Дифферинцируемость аттракторов возможно в нескольких направлениях, однако существуют исключения,например, пыль Кантора.
При поддержке инвариантных случайных вероятностных мер типа Синай-Рюэля-Боуэн странные аттракторы становится возможным найти в присутствии шума, если они размещены в оной.
Примерами странных аттракторов являются: дважды прокрученный в себя аттрактор, аттрактор Хенона, аттрактор Лоренца и аттрактор Росслера.
Эдвард Лоренц тоже свой вклад внёс в 1963 году после доказательства того, что простейшая система, состоящая из трех нелинейных дифференциальных уравнений, может привести к траекториям хаотического характера. Спустя несколько десятилетий работы Лоренца стали общим достоянием. Он стал первооткрывателем одного из примеров детерминированного хаоса в диссипативных системах. Хаотическое поведение позже было выявлено при расширении их размерности в множестве элементарных моделей биологических систем, решения которых колебательные, в том числе в моделях взаимодействия видов, моделях гликолиза и клеточного цикла, моделях ферментативного катализа и других. Именно на примере аттрактора Лоренца основано наше исследование.
Параметры, используемые в данной статье:
– отношение коэффициента кинематической вязкости к коэффициенту температуропроводности σ=10
– нормированное число Рэлея r=27
– коэффициент, содержащий информацию о геометрии конвективной ячейки b= ![]()
После ввода данных и подстановки в MathCad:
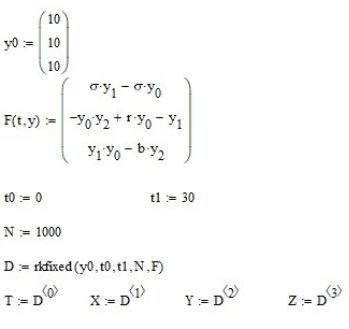
По полученному множеству решений создано визуализированное изображение:
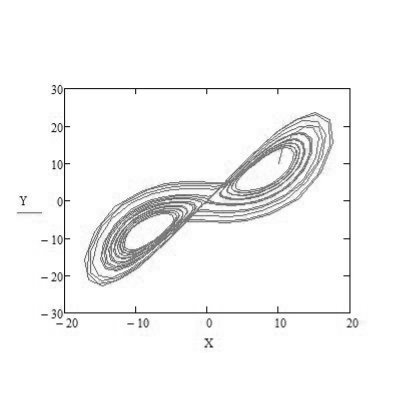
Рис. 1. Странный аттрактор Лоренца 1
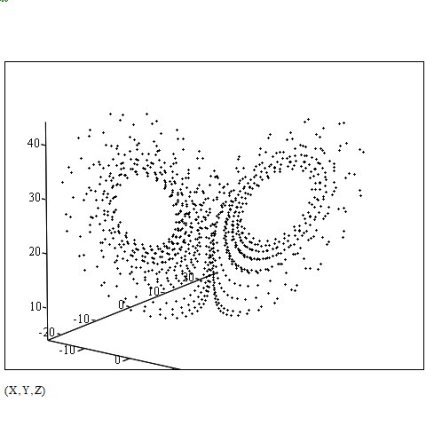
Рис. 2. Трёхмерное представление аттрактора 1
Литература:
- P. M. Кроновер. Фракталы и хаос в динамических системах. Основы теории. Москва: Постмаркет, 2000. — 352 с.
- Ильяшенко Ю. С. Аттракторы и их фрактальная размерность. — М.: МЦНМО, 2005. — 16 с
- А. П. Кузнецов, А. В. Савин, Ю. В. Седова Бифуркация Богданова — Такенса: от непрерывной к дискретной модели Изв. вузов «ПНД», т. 17, № 6, 2009 УДК 517.9

