Моделирование, как метод научного познания, пожалуй, является наилучшим способом изучения объектов и различных процессов, встречаемых в реальности. Оно основывается на создании моделей — неких абстрактных сущностей или приближенных копий, которые отражают все необходимые для исследования свойства изучаемых объектов.
Моделирование применяется практически повсеместно: оно позволяет, например, наглядно отобразить некоторые процессы для удобного восприятия, предугадать поведение реального объекта или же воспроизвести те события, которые в теории не могут произойти вовсе. Иными словами, моделирование играет крайне значимую роль в разных сферах: на производстве, в научно-исследовательской, инженерной и любой другой деятельности.
В рамках программирования под моделью следует понимать описание объектов, явлений, событий на строго определенном языке или в виде структуры данных. Такое описание может содержать все, что угодно: геометрических данные объекта, положения точки наблюдателя, информацию об освещении и т. д.
Компьютерная графика способствовала значительному развитию моделирования, поскольку она позволяет изобразить объекты любой природы, в том числе и абстрактные. Компьютерные модели уже давно стали незаменимым инструментом моделирования, особенно там, где изучение реальных объектов напрямую затруднено из-за физических или финансовых препятствий: в астрофизике, биохимии и т. д. Изучать подобные виртуальные модели значительно проще.
Основная сложность моделирования заключается в верных математических расчетах, поскольку необходимо, чтобы математическая зависимость модели была достаточно точно приближена к реальному поведению того или иного объекта. Помимо этого, результаты моделирования необходимо представить в визуальном виде, удобном для зрительного восприятия.
Визуализация — способ представления информации в виде структурных схем, карт, 3D-моделей и т. д. — является важным этапом в моделировании. Ее главной функцией является обеспечение удобного представления модели для зрительного наблюдения и анализа. Благодаря ей исследователь может буквально одним взглядом обнаружить особенности, выявить закономерности и аномалии в больших объемах информации.
Все большую и большую роль визуализация начинает играть в образовательном процессе, поскольку она позволяет решить крайне весомую проблему: учебники с информацией, представленные в виде неких иллюстраций в предельно абстрактном виде, морально устарели. Зачастую некоторые книги содержат только формулы и графики, которые воспринимаются учащимися с определенным трудом.
Визуализация результатов моделирования в программировании играет особую роль, если речь идет о моделировании физических процессов, где их наглядное представление является необходимым. Она позволяет «оживить» алгоритмы, описывающие те или иные законы, тем самым обеспечивая их хорошее восприятие.
Однако, для визуализации необходимо использовать определенные графические средства. Существует огромное множество различных фреймворков и библиотек, таких как Qt, Box2d, SDL, OpenGL, каждый из которых имеет свои недостатки и достоинства. Одной из самых популярных графических библиотек, пожалуй, является SFML (Simple and Fast Multimedia Library). Ее распространенность объясняется простотой и универсальностью: SFML позволяет достаточно легко связать вычисления, описанные в алгоритмах и свои графические возможности. SFML содержит 5 модулей:
– System — управление временем и потоками, он является обязательным, так как все модули зависят от него.
– Window — управление окнами и взаимодействием с пользователем.
– Graphics — делает простым отображение графических примитивов и изображений.
– Audio — предоставляет интерфейс для управления звуком.
– Network — для сетевых приложений.
Логика любой программы, основанной на использовании SFML, строится вокруг т. н. игрового цикла — серии повторяющихся тиков (кадров), в котором последовательно происходят все события за одну итерацию.
SFML обладает достаточно удобными и гибкими методами отрисовки различных примитивов (таких, как линии, круги, многоугольники, и т. д.), а также возможностью изменять их различные параметры (положение, цвет, размер, текстура и т. д.). SFML представляет из себя объектно-ориентированный аналог SDL с более расширенным функционалом. Несмотря на то, что такие крупные фреймворки, как Box2d имеет еще больше возможностей и обеспечивают куда более высокоуровневое взаимодействие с пишущим программу, следует понимать, что их «масштаб» также различен. Поэтому будет несколько некорректным сравнение целого фреймворка с графической библиотекой.
Для начала необходимо определить свойства окна, где будут отображаться все процессы и начальные параметры.
Анимация воспроизводится с помощью поочередной смены кадров в игровом цикле, описанном выше. Если мы на каждой итерации будем изменять координаты (x, y) объекта, то сможем привести его в движение. Но для этого необходимо воспользоваться ключевыми в SFML методами: clear(), draw(), display() Они отвечают за очистку окна, отрисовку объекта, отображению соответственно. При том, правильным тоном считается выполнение этих методов в том же порядке.
Рассмотрим в качестве примера программу, моделирующую движение небесных тел по законам небесной механики в упрощенном двумерном виде. Иначе говоря, все объекты (планеты, звезды и т. д.) в этой программе двигаются согласно трем законам механического движения и закону гравитации.
Небесная механика также включает в себя законы Кеплера (первый закон: орбита планеты имеют форму эллипса, в одном из фокусов которого располагается Солнце; второй закон: радиус-вектор планеты за равное время описывают одинаковые площади), однако они все были обобщены в законе всемирного тяготения Ньютона, поэтому нет необходимости их учитывать. Более того, с помощью законов Кеплера удобнее рассматривать взаимодействие лишь двух тел.
Стоит также оговорить, что некоторые параметры далеки от действительных в силу наглядности (размер небесных тел, расстояние между ними).
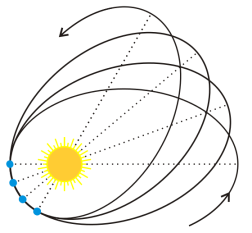
Рис. 1. Прецессия эллиптической орбиты
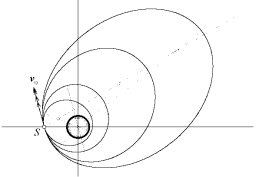
Рис. 2. Эллиптические орбиты тел, запущенных из одной точки в одном направлении с разными по модулю начальными скоростями
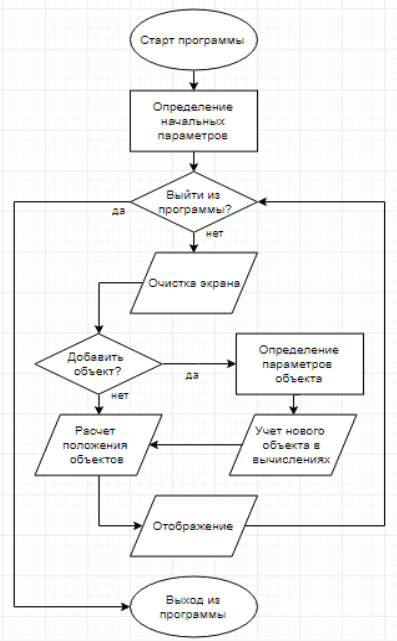
Рис. 3. Упрощенная блок-схема программы.
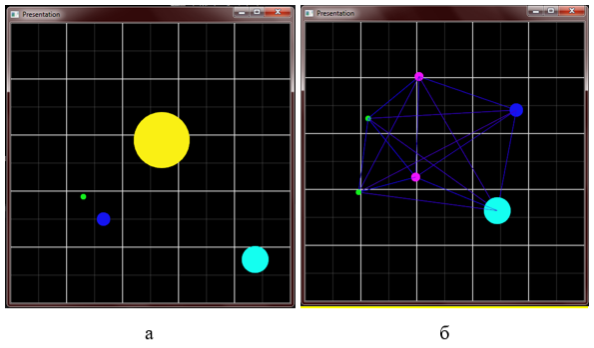
Рис. 4. Пример работы программы
Модель демонстрирует нам, что орбиты обращения планет вокруг светил имеют форму эллипса, и более того, сами орбиты обладают прецессией (т. е. они обращаются вокруг центра масс в фокусе с некоторым периодом). Также скорость движения планеты изменяется при приближении к звезде. Все эти наблюдаемые явления удовлетворяют законам небесной механики.
Можно сделать вывод о том, что представленные возможности SFML хорошо подходят для визуализации. Однако, эта библиотека не лишена недостатков. Например, метод clear(), очищает весь экран целиком. Это накладывает некоторые ограничения в тех случаях, когда требуется удалять с окна лишь один объект, а не все его содержимое.
Литература:
- Официальный сайт с документации для библиотеки SFML — URL: https://www.sfml-dev.org/
- Храмченков Е. В., Коптенок Е. В., Храмченко В. Д. Использование средств библиотеки SFML для написания игровых проектов // Техника. Технологии. Инженерия. — 2018. — № 2. — С. 18–22.
- Годограф скорости при кеплеровом движении — URL: https://refdb.ru/look/2212835-p2.html

