В статье рассматривается задача моделирования полёта квадрокоптера на базе рамы F450 (APM). Разработаны математические модели движения аппарата по вертикали (взлёт) и в вертикальной плоскости по траектории в виде ломаной. Математические модели реализованы в среде SolidWorks Motion для управления движением cсоответствующей3D модели.
Ключевые слова: квадрокоптер, среда моделирования SolidWorks Motion, движение твердого тела, управление движением.
Среди методов управления беспилотными летательными аппаратами следует выделить две основные группы: 1) методы, основанные на использовании управляющих воздействий в аналитической форме [1, 2]; 2) методы, использующие ПИД-регуляторы. Вторая группа методов требует привлечения средств численного и натурного моделирования [3] для адекватного определения коэффициентов регулятора. Чаще всего для численного моделирования используются системы Matlab Simulink и Universal Mechanism [4,5].
В данной работе ставится следующая цель: на базе разработанной ранее 3D модели [6] и управляющих воздействий в известной аналитической форме сформировать модель движения квадрокоптера в среде SolidWorks Motion.
Положение квадрокоптера в пространстве будем определять координатами x, y, z центра масс аппарата в неподвижной системе декартовых координат и тремя углами поворота вокруг главных центральных осей инерции квадрокоптера (xx, yy, zz): — угол рыскания, — угол крена, ![]() угол тангажа [7].
угол тангажа [7].
Уравнения, описывающие движение аппарата, записываются в виде [4]:
![]() ,
,
![]()
![]() (1)
(1)
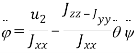 ,
,
![]() ,
,
![]() .
.
Здесь![]() — линейное, а
— линейное, а ![]() ,
, ![]() ,
, ![]() — угловые ускорения,
— угловые ускорения, ![]() — ускорение свободного падения,
— ускорение свободного падения, ![]() — масса аппарата,
— масса аппарата, ![]() ,
, ![]() ,
,![]() — главные моменты инерции аппарата;
— главные моменты инерции аппарата; ![]() ,
, ![]() и
и ![]() — управляющие параметры:
— управляющие параметры: ![]() - сила, действующая вдоль оси zz аппарата,
- сила, действующая вдоль оси zz аппарата, ![]() и
и ![]() — моменты относительно осей xx, yy, zz. Через силы тяги
— моменты относительно осей xx, yy, zz. Через силы тяги ![]() ,
,![]() ,
, ![]() ,
, ![]() создаваемые винтами квадрокоптера, управляющие параметры определяются следующим образом:
создаваемые винтами квадрокоптера, управляющие параметры определяются следующим образом:
|
|
где ![]() — расстояние от осей винтов до центра тяжести квадрокоптера,
— расстояние от осей винтов до центра тяжести квадрокоптера, ![]() — коэффициент пропорциональности между тягами винтов и реактивными моментами вращения относительно осей моторов.
— коэффициент пропорциональности между тягами винтов и реактивными моментами вращения относительно осей моторов.
Задача 1. Рассмотрим простой способ управления, для которого:
![]()
В этом случае управление ![]() амплитуда A определяется из условия
амплитуда A определяется из условия ![]() , где T — заданное время подъема на высоту h.
, где T — заданное время подъема на высоту h.
Задача 2. Рассмотрим одномерную задачу для подъема квадрокоптера на заданную высоту. В этом случае задача сводится к поиску такого управления ![]() , которое обеспечивало бы экспоненциальную сходимость к нулю отклонения
, которое обеспечивало бы экспоненциальную сходимость к нулю отклонения
![]() .
.
Здесь ![]() — желаемое, а
— желаемое, а ![]() — фактическое положение аппарата. Искомое управление может быть найдено из решения дифференциального уравнения [7]:
— фактическое положение аппарата. Искомое управление может быть найдено из решения дифференциального уравнения [7]:
Уравнение (2) можно привести к каноническому виду:
![]()
тогда коэффициенты ![]() и
и ![]() могут быть назначены исходя из очевидного физического смысла этого уравнения.
могут быть назначены исходя из очевидного физического смысла этого уравнения.
В нашем случае решение дифференциального уравнения выглядит следующим образом [7]:
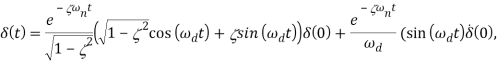
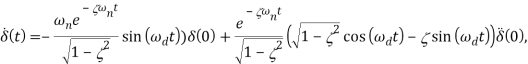
![]() .
.
Следовательно,
![]() .
.
На Рис.1 показаны результаты моделирования в среде SolidWorks Motion [8] для подъема квадрокоптера в соответствии с математической моделью для задачи 1, а на Рис.2 — для задачи 2. Необходимое управление в каждом из этих случаев формировалось при помощи конструктора уравнений SolidWorks Motion.
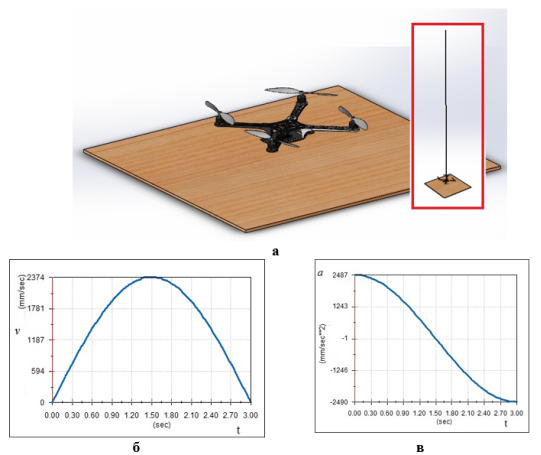
Рис. 1. Задача 1. Траектория подъема квадрокоптера на заданную высоту (a), скорость движения (б), ускорение движения (б)
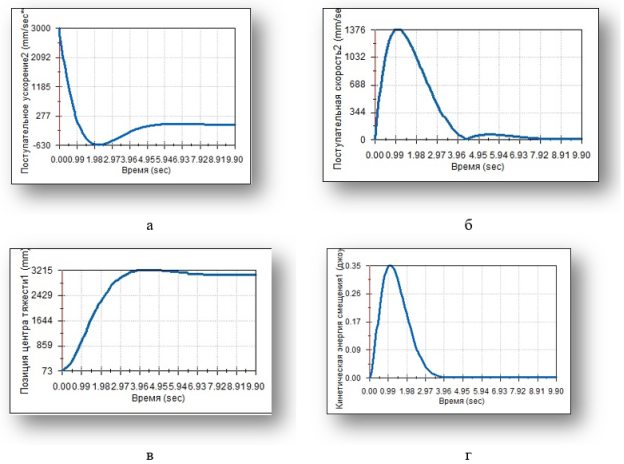
Рис. 2. Задача 2. Результаты анализа движения для задачи 1: поступательное ускорение (а), поступательная скорость (б), позиция центра тяжести (по высоте) (в), кинетическая энергия (г)
В каждом случае масса аппарата m= 3.674 кг., ускорение свободного падения g=9.80676 м/сек2, =0.7, n=1рад/сек, высота подъема h=3м.
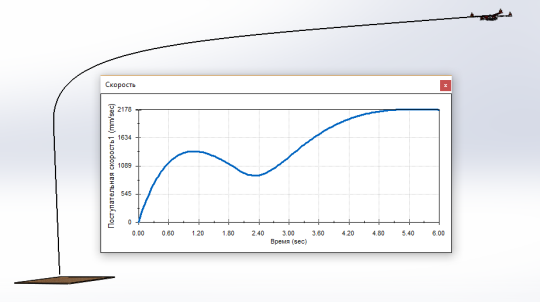
Рис. 3. Траектория движения и поступательная скорость полёта в вертиуальной плоскости
Задача 3. На рис.3 показана траектория движения квадрокоптера по желаемой траектории, заданной двумя звеньями ломаной: вертикально вверх на 3 м., а затем — горизонтально на 6 м. Математическая модель движения была построена аналогично задаче 2. На рис. 3 представлены результаты моделирования.
Литература:
1. Белоконь С. А., Золотухин Ю. Н., Мальцев А. С., Нестеров А. А., Филиппов М. Н., Ян А. П. Управление параметрами полета квадрокоптера при движении по заданной траектории // Автометрия. 2012. Т. 48, № 5. С. 32–41.
2. Дивеев А. И., Конырбаев Н. Б. Применение метода вариационного аналитического программирования для синтеза управления летающим роботом // Фундаментальные исследования. 2015,.№ 3. С. 51–57.
3. Aminurrashid Noordin, Mohd Ariffanan Mohd Basri, Zaharuddin Mohamed and Amar Faiz Zainal Abidin Modelling and PSO Fine-tuned PID Control of Quadrotor UAV// International Journal on Advanced Science, Engineering and Information Technology. 2017, Vol 7, Iss 4, PP 1367–1373.
4. Гэн К., Чулин Н. А. Наука и Образование. МГТУ им. Н. Э. Баумана. Электрон. журн. 2015, № 05. С. 218–235. DOI: 10.7463/0515.0771076.
5. Гурьянов А. Е. Моделирование управления квадрокоптером// Инженерный вестник. 2014. № 08, Режим доступа: http://engsi.ru/doc/723331.html
6. Попков М. А., Чугунов М. В. Проектирование и оптимизация несущей системы квадрокоптера // Молодой ученый. — 2018. — № 14. — С. 30–35. — URL https://moluch.ru/archive/200/49131/
7. Б. П. Демидович Краткий курс высшей математики: Учеб. пособие для вузов / Б. П. Демидович, В. А. Кудрявцев. — М.: ООО «Издательство Астрель»; ООО «Издательство АСТ», 2001. — 656 с.
8. Алямовский А. А. Инженерные расчеты в SolidWorks Simulation. М.: ДМК Пресс, 2010. 464 с., ил. (Серия «Проектирование»).
[1] Работа выполнена при поддержке Фонда содействия развитию малых форм предприятий в научно — технической сфере по программе УМНИК Aero.NET, договор № 11548ГУ/2017 «Разработка интегрированной модельной среды для квадрокоптера в среде SolidWorks»







 ,
,
