В последние несколько лет активное развитие в области анализа и оценки инвестиционной привлекательности комплексных инновационных проектов получили методы, основанные на теории реальных опционов. Использование таких методов позволяет оценить управленческую гибкость, т.е. оценить влияние управленческих решений, принимаемых в ходе реализации оцениваемого проекта, на привлекательность этого проекта.
Под реальными опционами принято понимать такие опционы, базовым активом для которых являются реальные активы фирмы. Впервые термин «реальный опцион» использовал Стюарт Майерс в своей работе «Determinants of Corporate Borrowing» [3], опубликованной в 1977 году, в которой он дал оригинальную трактовку самой сущности реальных опционов.
К настоящему времени было разработано достаточно большое количество методов и моделей оценки стоимости реальных опционов, причем большинство из них основывается либо на методе конечных разностей и дифференциальных уравнениях с частными производными, либо на методах решетки, либо на методах имитационного моделирования.
Биномиальная модель является одним из фундаментальных и наиболее распространенных дискретных методов оценки стоимости реальных опционов и является ярким примером методов решетки. Она была разработана Джоном Коксом, Стивеном Россом и Марком Рубинштейном и описана в их работе «Option Pricing: A Simplified Approach» [2].
Относительная простота используемого в ней математического аппарата и высокая точность получаемых результатов сделали ее одним из стандартов де-факто в области оценки стоимости реальных опционов.
По мере развития программного обеспечения для работы с электронными таблицами и автоматизации функций финансового анализа, было автоматизировано и построение биномиальных моделей. В сети Internet и публикациях, посвященных автоматизации инвестиционных и финансовых расчетов, можно найти большое количество работоспособных с технической точки зрения и корректных с точки зрения логики построения модели приложений и скриптов, использование которых позволяет рассчитать стоимость опциона с помощью биномиальной модели в соответствии с оригинальным алгоритмом, предложенным авторами метода. Следует, однако, отметить, что большинство из них имеют весьма незначительные отличия с точки зрения конечного пользователя – причем речь здесь идет не столько об используемом алгоритме (очевидно, что его изменение чревато несоответствием оригинальной модели), сколько о представлении входных параметров и результатов выполнения модели.
В рамках данной работы предлагается изменить порядок визуализации деревьев стоимости базового актива и реального опциона для того, чтобы нагляднее продемонстрировать связь структуры дерева стоимости реального опциона и его узлов с соответствующими им элементами дерева стоимости базового актива.
Описываемая реализация алгоритма построения дерева стоимости опциона и расчета составляющих его узлов отражает следующие аспекты применения биномиальной модели:
· Последовательное разворачивание дерева стоимости базового актива и расчет его узлов;
· Построение дерева стоимости реального опциона и определение значений узлов этого дерева на основе построенного ранее дерева стоимости базового актива;
· Последовательное сворачивание дерева стоимости реального опциона в конечную точку – искомую стоимость реального опциона.
Особенностью предлагаемой реализации является визуализация дерева стоимости реального опциона и его расположение относительно дерева стоимости базового актива:
· Узел первоначальной стоимости базового актива располагается слева, узел искомой стоимости реального опциона – справа;
· Разворачивание дерева стоимости базового актива и сворачивание дерева стоимости реального опциона производится слева направо в горизонтальной плоскости, ветвление деревьев осуществляется в вертикальной плоскости;
· Каждый узел дерева стоимости реального опциона располагается на том же горизонтальном уровне, на котором расположен соответствующий ему узел дерева стоимости базового актива.
Подобный подход к порядку построения и отображения деревьев стоимости базового актива и реального опциона позволяет с одной стороны отделить деревья друг от друга и с другой стороны – сохранить логическую связь узлов деревьев на их графическом представлении.
Для наглядной иллюстрации данного подхода, рассмотрим пример, описанный в работе Томаса Коупленда и Питера Туфано «A Real-World Way to Manage Real Options» [1, 93-96] и ставший одним из классических в исследованиях, посвященных оценке стоимости реальных опционов. Согласно условиям задачи, рассматривается проект строительства нового завода. Инвестиционные затраты на подготовительном этапе оцениваются в 60 млн. долл., в случае выполнения этого этапа, в конце года компания может инвестировать 400 млн. долл. в проектирование завода и, наконец, после завершения этапа проектирования, компания может инвестировать 800 млн. долл. в строительство завода в течение последующих двух лет. Приведенная стоимость построенного завода составляет 1 млрд. долл. Безрисковая ставка равна 8%, волатильность – 18,23%.
Построенные деревья стоимости базового актива и реального опциона изображены на рисунке 1.
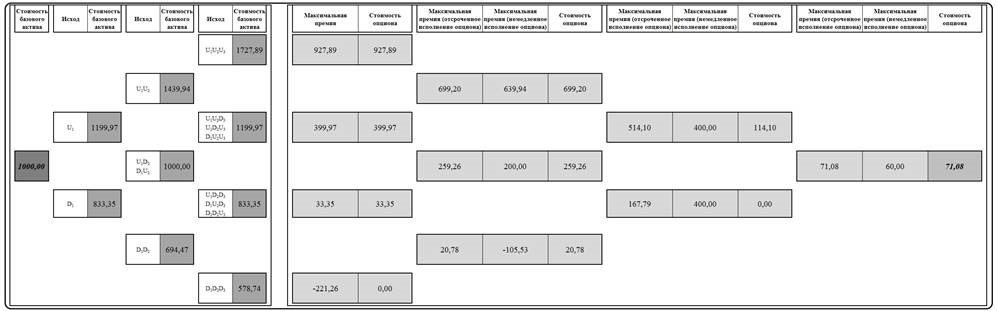
Рисунок 1. Пример графического изображения биномиальных деревьев стоимости базового актива и реального опциона.
Следует отметить, что методика использования деревьев и расчета значений их узлов не изменяется, т.е. используется традиционный метод, предложенный Коксом, Россом и Рубинштейном (бинарное изменение прогнозируемой стоимости базового актива в каждом следующем периоде для каждой альтернативы текущего периода – увеличение или уменьшение стоимости в соответствии с определенным значением коэффициента) и описанный в работе Коупленда и Туфано. Отличие касается не логического, а графического аспекта расчета стоимости опциона графическим методом.
Графическое представление структуры дерева стоимости реального опциона является зеркально отраженным по отношению к представлению структуры дерева базового актива: конечные узлы дерева опциона расположены слева, непосредственно рядом с конечными узлами дерева стоимости базового актива, которым они соответствуют, а узел искомой стоимости опциона находится справа.
После построения структуры дерева стоимости реального опциона, выполняется расчет его узлов и определяется экономическая целесообразность исполнения опциона в каждом периоде для каждой из альтернатив. Сворачивание дерева стоимости реального опциона завершается в его конечном узле, значение которого и является искомой стоимостью опциона.
Техническая реализация выполняется с использованием программного обеспечения Microsoft Excel, которое активно используется аналитиками и менеджерами для выполнения различных расчетов, построения и визуализации отчетов.
Следует также отметить простоту реализации предложенного решения: для построения модели в среде Microsoft Excel достаточно общих навыков работы с электронным табличным процессором (работа с ячейками и массивами, использование стандартных математических и логических формул). В случае наличия навыков программирования на языке VBA (Visual Basic for Applications) возможно повышение степени автоматизации описанной модели.
Кроме того, техническая реализация обладает высокой гибкостью: так, например, описанный подход может быть эффективно использован для построения полиномиальных моделей с фиксированным или плавающим количеством возможных исходов в различных периодах.
Литература:
1. Copeland T. E., Tufano P. A Real-World Way to Manage Real Options // Harvard Business Review. 2004. Vol. 82, Issue 3. P. 90-99.
2. Cox J., Ross S., Rubinstein M. Option Pricing: A Simplified Approach // Journal of Financial Economics. 1979. Vol. 7, Issue 3. P. 229–263.
3. Myers S. C. Determinants of Corporate Borrowing // Journal of Financial Economics. 1977. Vol. 5, Issue 2. P. 147-175.







