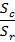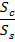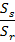Elastic averaging concept applied to multilayer epicyclical gearboxes

Abstract:This work investigates the possibility of increasing the torque rating of epicyclical gearboxes through application of an elastic averaging concept. The goal is a uniform distribution of the loads transmitted by each layer of planetary gears. Authors studied major factors affecting the non-uniformity of the loads for the case of a double-layer gearbox and offer design recommendations based on the results of their parametric analyses.

Keywords:epicyclical gearbox, elastic averaging, stiffness in torsion

1. INTRODUCTION

The oilfield industry’s increasingly high standards for directional drilling and measurement tools are challenging to designers, who must continually innovate their engineering to achieve the required specifications. One example is the epicyclical gearboxes widely used in these tools for position control. The gearboxes must reliably survive very high torques for relatively long drilling times in harsh conditions.

To meet this challenge we consider the possibility of increasing the torque capacity of epicyclical gearboxes for a given constraint on the maximum diameter of the ring gear, dictated by the wellbore size.

Given the diameter limitation, only the length of the gearbox could be used to increase its strength. However, elongation of planetary gears does not solve the problem: longer planets experience less uniform distribution of the load along the teeth. This is explained by the significant differences in rotational and bending stiffness of planetary, sun and ring gears.

The gearbox design in our study uses two or more planetary gear layers. In such a design, the increased number of planets should decrease the loads transmitted by the gear teeth.

A known problem of such a solution is the non-uniform distribution of the load among layers of the planets [1], [2]. In other words, planets in one layer transmit higher torque than those in other layers. As a result, the benefit derived by increasing the number of planets does not justify the subsequent increase in manufacturing complexity. To overcome this issue, we introduced an elastic averaging concept that enables us to vary the design parameters in such a way as to transmit the torque as uniformly as possible. Parameters included relative stiffness of the ring and sun gears and carrier in torsion; gear ratio; and number of planets in the layers. In this paper we present only the analyses of the two-layer gearbox design.

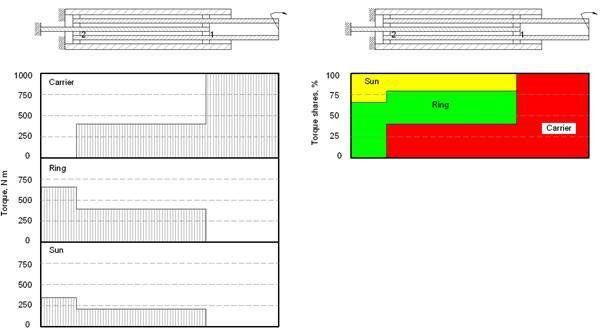
Fig. 1 An example of torque diagram and load sharing for a two-layer gearbox

2. METHODOLOGY

A torque diagram, illustrating transmission of the load from the carrier to the sun and the ring gears is shown in Fig. 1. The difference between deformations of torsion shown in Sections 1 and 2 for the carrier, ring, and sun gear are written as

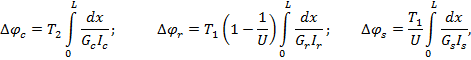
where T₁, T₂ are torque shares taken by the first and second layers; 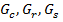 are shear modules of the carrier, ring, and sun gear materials; 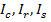are polar moments of inertia of the carrier, ring, and sun gear sections;  is the elementary length; L is the length between layers of the planetary gears; and U is the gear ratio.

In the ideal case all the deformations are equal and the load between the two layers is distributed equally. This condition is written as

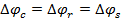                                                                                                                  (1)

Now consider the additional parameters: stiffness in torsion between layers of the carrier, ring, and sun gears:

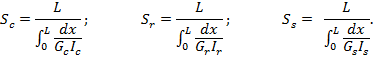
Using these parameters, the conditions in Eq. 1 transform to

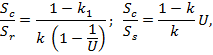
where 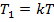 and 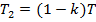 ;  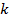is a coefficient showing the share of the torque taken by the first layer.

Consider a numerical example: k = 0.4 (this could be, for instance, when N₁ = 4 – number of planets in the first row, N₂ = 6 – number of planets in the second row); gear ratio U = 32:11. In this case:

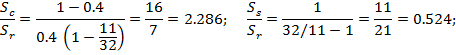
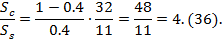
Therefore, for this particular case stiffness of the carrier should be 2.286 times the stiffness of the ring. There is no need to explain how challenging this would be: the ring gear is located externally, meaning significantly higher polar moments of inertia. By changing allocation of planets in the two layers, however, one could make the mismatch a minimum. This is demonstrated in Table 1, which shows calculations for all the possible combinations.

Table 1 – Relative stiffness required to satisfy conditions of Eq. 1

As seen from Table 1, the best result in terms of carrier to ring stiffness ratio is achieved for the following combination N₁-N₂: 8:3. In this case, however, stiffness of the carrier should be nearly equal to the stiffness of the sun. Next options in order of preference will be 8:4 and 6:3. Here, the carrier should be 45.5% stiffer than the sun, which is achievable. The overall conclusion is that it is preferable for the number of planets in the first row to be bigger than in the second one. The final selection of the planet arrangement should also consider other factors. For example, if there are too many planets in a layer, the load will be distributed less uniformly among them, or the carrier will be too weak because of the sheer number of windows.

As seen, it is practically impossible for the conditions of Eq. 1 to be completely satisfied. This is explained by the fact that number of planets can only be an integer.

The next step requires management of the stiffness ratios. If there is an elastic mismatch between sun, carrier, and ring, these parts will deform differently under torque. As a result, the planets will deform even more to accommodate the mismatch. Assume for simplicity that connections between planets and carrier are absolutely rigid. If the planets are absolutely elastic, then the carrier, sun, and ring will have different relative deformations defined by the following relationships:

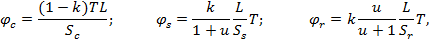
where relative twist angles are defined with respect to the twist angles of the second row; 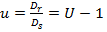 is ratio of the ring gear and sun gear diameters.

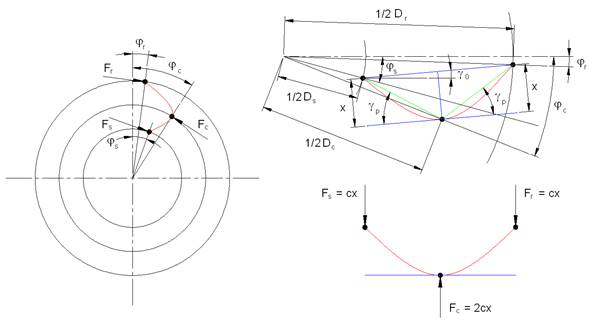
Fig. 2 Schematic diagram of the additional deformations of a planetary gear

However, in reality the planets are not flexible. As a result of dissimilar deformation of the carrier, sun, and ring, the planets will deform as shown in Fig. 2, leading to additional elastic reactions. Assume all the deformations are small. In such a case the reactions of the planet (on the ring and sun) may be considered equal and directed tangentially to the corresponding circles.

Motion of the contact points of the planet consists of two components: rotation with angle, 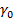, and deformation,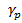. Rotation of the planet is defined by relative deformation of ring and sun:

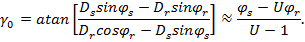
Bending deformation of the planet is expressed as

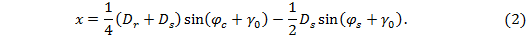
Assume that equivalent bending stiffness,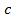, has the same value for the pairs of planet-sun and planet-ring. In such a case, forces  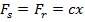  will work to increase the twisting of the sun and ring, and force  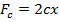will work to decrease deformation of the carrier. Stiffness of the tooth can be estimated using the plain-strain finite-element analysis [2].

Therefore, additional torques will have values as shown:

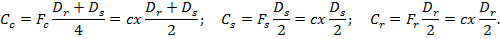
Given these torques, deformations of the carrier, sun, and ring will change, such that

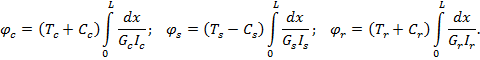
The load multiplication factor that is due to the stiffness mismatch for the teeth contacts can be estimated as follows:

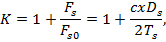
where 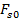 is the theoretical force for perfectly matching deformations (or absolutely flexible planets).

The numerical example below illustrates major findings of the study. Consider a gearbox with the following input parameters: u = 1.5 (U = 2.5); T = 1000 N×m; 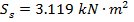; ; 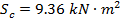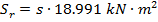, where s is a variable coefficient (parameter);  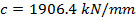; L = 50 mm; diameter of the sun D_s = 30 mm.

Fig. 3 shows change of the load factor K versus share of the load, k, taken by the first row (s   = 1). As seen, increasing the value of k results in a lower load factor, K (better for bending strength of the planet teeth). The optimum is achieved for this design at k » 0.6 (i.e., first row takes approximately 60% of torque), where K = 1.

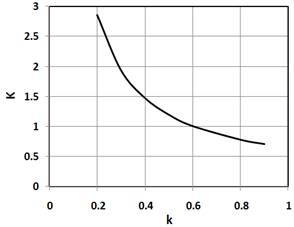
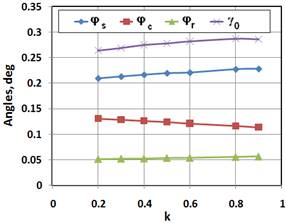
Fig. 3 Load factor K vs. load share k                    Fig. 4 Angles vs. load share k

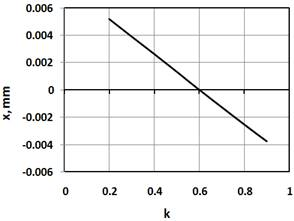
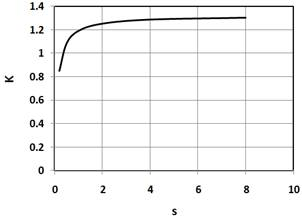
Fig. 5 Deformations x vs. load share k                Fig. 6 Load factor K vs. parameter s

Fig. 4 shows how the angles change with respect to k. Note that the larger values of k result in larger angles of planet rotation, 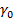. As a result, even though elastic deformations grow, deformations of the planets decrease (Fig. 5). Therefore, angle  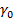 relieves stress on the planets.

Fig. 6 illustrates the effect of the ring stiffness on the load factor, K. A stiffer ring (larger s) leads to higher K values. As expected, balance is achieved when the stiffness of the ring is approximately equal to the stiffness of the carrier.

We concluded the following:

·         Elastic mismatch results in higher gear loading.

·         The planets are able to rotate; therefore, the problem is nonlinear.

·         Optimization is possible with the goal of minimizing gear loads (major factors of influence are load-sharing among rows; stiffnesses of the ring, carrier, and sun; and gear ratio).

There is one more condition for even load-share (i.e., no additional loading of the planets), which states x = 0, and means that stiffness of the parts are selected such that under torsion planets rotate without deformation. From Eq. 2, assuming that angles 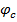 and 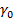 are small, after transformations, the following condition is derived

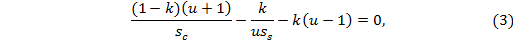
where 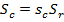 and .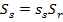

In reality the left side of the Eq. 3 may not be equal to zero but to some finite value

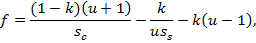
and the purpose of optimization would be written as

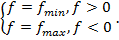
Fig. 7 shows the effect of load-share ratio k and ratio u on the value of the parameter f for fixed stiffness ratios 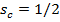 and 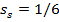. One can conclude that higher values of k and lower values of u lead to lower values of f.

Fig. 8 shows the effect of carrier stiffness ratio, 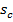, and load-share ratio, k, on the value of  f for a fixed value of u = 3. The conclusion: increasing stiffness of the carrier leads to a drop in the value of f for any k. As a result, at lower k it is best to increase the stiffness of the carrier to minimize f. At higher k it is possible to achieve f = 0. Depending on k, this can be achieved by either increasing or decreasing the stiffness of the carrier. It is more advantageous to have higher k, since in this case the optimum would be achieved at more realistic ratios of .

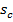To illustrate, we solve the condition of optimum with respect to :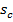

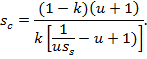
Fig. 9 shows the optimum values of 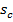 versus k for u = 3 and set of values of  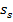(1/8, 1/10, 1/12 and 1/14). As seen, higher k leads to lower values of 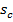. At 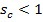 the carrier should be less stiff than the ring, which is easier to achieve.

Fig. 10 shows the optimum values of 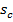 versus k for  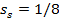and a set of different values of u (1.5–4.5). This diagram illustrates why at certain combinations of k and u optimum is not physically achievable (where 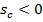, which means negative stiffness of the carrier).

Fig. 11 shows the effect of the carrier stiffness parameter, s_c, and ratios, u, on the parameter f for k = 0.6 and 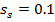. As seen, it is advantageous to decrease gear ratios to obtain an f that is closer to zero.

Fig. 12 presents the effect of the sun stiffness factor, s_s, and load-share ratio, k, on the parameter f for s_c = 0.5 and u = 3.

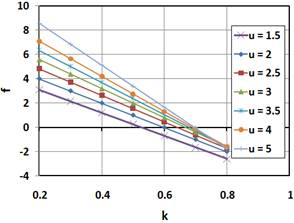
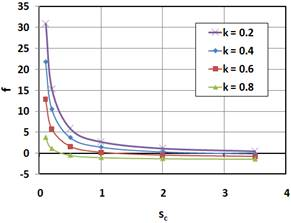
               Fig. 7 Parameter f vs. k and u                             Fig. 8 Parameter f vs. k and s_c

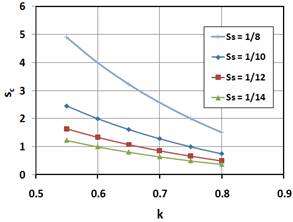
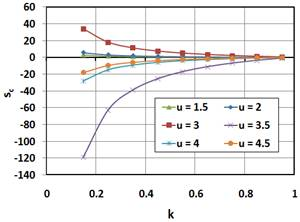
              Fig. 9 Optimum s_c vs. k and s_s                       Fig. 10 Optimum s_c vs. k and u

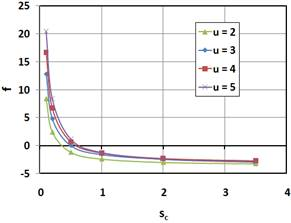
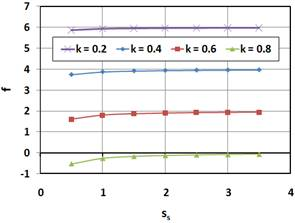
              Fig. 11 Parameter f vs. s_c and u                         Fig. 12 Parameter f vs. s_s and k

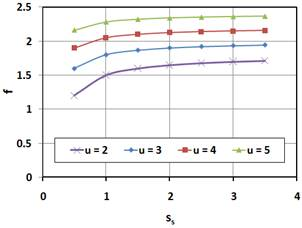
                Fig. 13 Parameter f vs. s_s and u

In Fig. 13 one can see the effect of the sun stiffness factor, s_s, and ratio of the diameters, u, on the parameter f for s_c = 0.5 and k = 0.6. The effect of the s_s stays nearly the same for given combinations of the other parameters. This means that relative stiffness of the sun with respect to stiffness of the ring plays a secondary role. Physically, this is explained by the fact that relative torsion of the sun and ring result in rotation of the planet without additional stress.

Our conclusion is the following: the additional loading of the teeth improves if:

·         gear ratio, U, decreases,

·         load share of the first row, k,  increases,

·         stiffness ratio of the ring and carrier is optimized for given values of k and U.

The stiffness ratio of the ring and carrier can be decreased as  follows:

·         Increase stiffness of the carrier: Elongate carrier by solid tubular sections such that integral stiffness is less affected by relatively flexible cut-outs for planetary gears, or use materials with higher shear modulus.

·         Decrease stiffness of the ring gear: Recess outer surface of the housing or use materials with lower shear modulus.

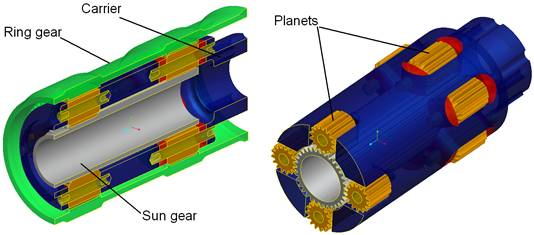
Fig. 14 Example of the two-layer gearbox design

Fig. 14 shows an example of a two-layer gearbox designed by applying the optimization rules just discussed. The first iteration of the design had four planets in the first layer, and six planets in the second, and no attempt was made to balance the stiffness in torsion. As a result, planets of the first layer were estimated to have a 20% higher teeth loading than those in the second. This estimation has been verified by a separate finite-element analysis of the full gear box assembly.

In the second iteration, by managing relative stiffness in torsion of the ring, carrier, and sun, and by selecting a favourable gear ratio and planet arrangement in the layers (six planets in the first layer and four in the second), we increased the estimated torque capacity of the gearbox by 67% with respect to the original design with one layer of six planets.

3. CONCLUSIONS

This article presents an elastic averaging concept that can be applied to the design of multi-layer epicyclical gearboxes. With this concept design parameters (gear ratio, allocation of planetary gears, materials and dimensions of the gears etc.) can be varied so that all the planets carry the same load. One can increase the torque capacity of the gearbox by elongating it and without increasing the outer diameter, which is a critical requirement for oilfield tools. The methodology developed in the study has been validated by a separate finite-element analysis performed for a double-layer epicyclical gearbox. Recommendations given in the paper can be used for parametric analyses when such gearboxes are designed.

References:

1.      Birger, I.A., Shorr, B.F., and Iosilevich G.B. Strength analysis of machine parts, 1979 (Mashinostroyeniye, Moscow – in Russian).

2.      Vulgakov, E.B. et al. Aviation gear transmissions and gearboxes, 1981 (Mashinostroyeniye, Moscow – in Russian).