В данной работе рассмотрена проблематика подсчета численности мобильного персонала на некотором предприятии, где весьма широкое и плодотворное применение имеют идеи и методы теории массового обслуживания, с помощью которых становится возможным провести количественный анализ функционирования многих сложных систем. Такой анализ позволяет:
- Выяснить зависимость важнейших характеристик системы, описывающих качество ее функционирования, от исходных характеристик (структуры системы, входящего потока, времени и дисциплины обслуживания и пр.);
- Решать задачу оптимального выбора исходных характеристик, критерием оптимальности которого является наиболее быстрое удовлетворение потребностей клиента.
Бизнес-процессы, которые описывают производство некоторого товара мобильными сотрудниками мы будем называть специальными.
Для специальных бизнес-процессов, с использованием производства некоторого товара мобильными сотрудниками, в данной статье мы будем исследовать систему, на основе математической модели массового обслуживания с накопителем. Данная система была выбрана, как расширение уже имеющегося набора решений, предоставленным в [2]. Как пример данного бизнес-процесса можно указать фургон по производству мороженого, у которого холодильник выступает в роли накопителя, а поток заявок будет стохастическим, так как люди покупают товар случайным образов в течении дня.
Предлагаемая математическая модель не повторяет ни одну из имеющихся и является синтезом моделей, используемых в теории массового обслуживания, теории управления персоналом, теории накапливания.
Существуют многочисленные распределительные системы, в которых производимый в период отсутствия запросов продукт помещается в накопитель.
Назначение накопителя в такой системе состоит в том, чтобы при случайном характере поступления заявок на продукт, во-первых, уменьшить простои сотрудника, производящего продукт, а во-вторых, уменьшить число отказов в удовлетворении заявок или время их ожидания. В данной ситуации, требование будет являться запросом на продукт покупателем.
Не менее важен вопрос выбора порядка обслуживания поступающих заявок. С этой целью интересно проанализировать следующие два варианта:
- Пришедшее требование отсылается в накопитель и за счет его запасов удовлетворяет спрос на продукт, а в случае, если этого запаса не хватает, отправляется сотруднику для того, чтобы непосредственно от него получить необходимое количество продукта;
- наоборот, требование сначала отсылается сотруднику, а если он занят, то в накопитель.
Рассмотренный здесь принцип, описывающий функционирование упомянутых систем, отличается от моделей управления запасами [1], поскольку пополнение запаса продукта в накопителе никем не регулируется и происходит в случайные моменты времени. Также она и не является чистой моделью массового обслуживания из-за присутствия в ней накопителя.
Системы обслуживания с накопителем «дискретного» типа
Рассмотрим системы массового обслуживания Q1 и Q2, в каждой из которых имеется один сотрудник, производящий продукт. Этот продукт, в периоды отсутствия запросов на него, поступает в накопитель (бункер) объема m, где ![]() При этом допустим, что единицы продукта сотрудник производит за случайное время
При этом допустим, что единицы продукта сотрудник производит за случайное время ![]() , распределенное по показательному закону с параметром
, распределенное по показательному закону с параметром ![]() . Входящий поток требований — рекурентный, т. к. он определяется единственным законом распределения и
. Входящий поток требований — рекурентный, т. к. он определяется единственным законом распределения и ![]() — функция распределения интервалов между моментами поступления требований. Каждому требованию нужна единица продукта. Если накопитель заполнен и запросов нет, сотрудник отдыхает и включается в работу, как только придет требование. В системе Q1 пришедшее требование обращается в накопитель и, если он не пуст, забирает там одну единицу готового продукта. Если же накопитель пуст, то требование отсылается к сотруднику и обслуживается им случайное время
— функция распределения интервалов между моментами поступления требований. Каждому требованию нужна единица продукта. Если накопитель заполнен и запросов нет, сотрудник отдыхает и включается в работу, как только придет требование. В системе Q1 пришедшее требование обращается в накопитель и, если он не пуст, забирает там одну единицу готового продукта. Если же накопитель пуст, то требование отсылается к сотруднику и обслуживается им случайное время ![]() . Требование, заставшее накопитель пустым, а сотрудника занятым, теряется.
. Требование, заставшее накопитель пустым, а сотрудника занятым, теряется.
В системе Q2 приходящее требование обращается сразу к сотруднику и, если он не занят, обслуживаются им случайное время ![]() . Если сотрудник занят, то требование отсылается в накопитель и, при условии, что он не пуст, заберет там единицу готового продукта. Если сотрудник занят, а накопитель пуст, то требование теряется.
. Если сотрудник занят, то требование отсылается в накопитель и, при условии, что он не пуст, заберет там единицу готового продукта. Если сотрудник занят, а накопитель пуст, то требование теряется.
Важнейшими характеристиками функционирования описанных систем являются вероятность потери требования и среднее число требований в накопителе.
Для описания системы ![]() рассмотрим состояние системы
рассмотрим состояние системы ![]() , где
, где ![]() , если в момент
, если в момент ![]() сотрудник в системе
сотрудник в системе ![]() свободен, и
свободен, и ![]() , если он занят;
, если он занят; ![]() — количество единиц продукта в накопителе системы
— количество единиц продукта в накопителе системы ![]() в момент
в момент ![]() .
.
Очевидно, что ![]() — процесс немарковский. Пусть
— процесс немарковский. Пусть ![]() — момент поступления в систему требования с номером S. Тогда значения процесса
— момент поступления в систему требования с номером S. Тогда значения процесса ![]() образуют вложенную цепь Маркова.
образуют вложенную цепь Маркова.
Обозначим ![]() вероятность того, что за время между моментами поступления требований сотрудник произведет j единиц продукта.
вероятность того, что за время между моментами поступления требований сотрудник произведет j единиц продукта.
Для решения похожей ситуации в работе [2] автор предлагает такую формулу:
![]()
Будем считать, что система Q1 в момент ![]() находится в состоянии
находится в состоянии ![]() , если
, если ![]() и в состоянии
и в состоянии ![]() , если
, если ![]() . В системе Q2 через
. В системе Q2 через ![]() обозначим ее состояние в момент
обозначим ее состояние в момент ![]() , если
, если ![]() .
.
Матрицы переходных вероятностей Марковских цепей ![]() и
и ![]() одинаковы и имеют вид
одинаковы и имеют вид
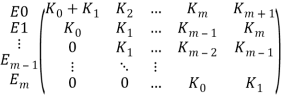
Пусть ![]() — вероятность того, что в момент
— вероятность того, что в момент ![]() система
система ![]() находится в состоянии
находится в состоянии ![]() .
.
Обозначим ![]() — производящую функцию распределения вероятностей
— производящую функцию распределения вероятностей ![]() . Нетрудно показать, что при условии
. Нетрудно показать, что при условии ![]() существуют пределы
существуют пределы
![]()
Задающее стационарное распределение вероятностей состояний цепи ![]()
Последнее, как легко видеть, удовлетворяет системе уравнений:
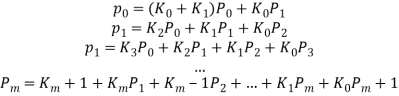 (1.1)
(1.1)
Пусть ![]() — производящая функцию распределения
— производящая функцию распределения ![]()
Умножив уравнение (1.1) последовательно на ![]() и сложив их, получим:
и сложив их, получим:
![]()
Отсюда, ![]() .
.
Так как ![]() , то
, то 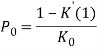
Заметим, что ![]()
Где, а — средняя длина интервала между моментами поступления требований.
Нетрудно видеть, что вероятность потерь требований в системах Q1 и Q2 одинаковы и равны
![]() (1.2)
(1.2)
Среднее число требований в накопителе системы Q1 равно:
![]() ,(1.3)
,(1.3)
где 
Среднее количество продукта в накопителе системе Q2 равно
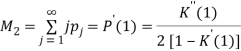 (1.4)
(1.4)
Сравнивая (1.3) и (1.4), находим, что ![]() .
.
Подводя итог данной статьи, была предложена модель для специальных бизнес-процессов с использованием производства некоторого товара мобильными сотрудниками в виде системы массового обслуживания с накопителем. В этой статье был проведен анализ такой системы с бесконечным накопителем двух видов Q1 и Q2, которые отличаются между собой порядком обслуживания поступающих заявок. Путем вычислений было установлено, что система Q1 является наиболее подходящей для данной задачи. Так как она позволяет удовлетворить больше заявок или снизить время их ожидания за тот же самый промежуток времени.
Литература:
- Калашников В. В., О некоторых результатах в теории запасов.
- Афанасьева Л. Г., Некоторые прикладные системы массового обслуживания и их оптимизации.

