Природа щедро наделила каждого ребенка возможностью развиваться. Дети с некоторой интеллектуальной недостаточностью на протяжении всей жизни развиваются независимо от степени тяжести дефекта. Своеобразие развития таких учащихся состоит в том, что оно затруднено как внешними, так и внутренними факторами: несоответствие уровня интеллектуального развития возрасту, недоразвитие мелкой моторики рук, плохая восприимчивость ко всему новому, слабая любознательность. Процессы сравнения и обобщения затруднены, отличаются слабостью логического анамнеза и синтеза, трудностью абстрагирования.
Развитие учебно-познавательных действий является основной целью коррекционно-воспитательного процесса. При этом особое значение имеет специальный подбор (с учетом особенностей развития детей) учебных заданий наглядного, предметно-практического и мыслительного характера. Для развития и коррекции личностного развития школьника необходимы системы коррекционной работы, использование ряда психолого-педагогических разработок, способов и приемов активизации мыслительной деятельности. Под коррекционной работой понимается исправление или ослабление недостатков психического и физического развития. Эффективностью исправления этих недостатков зависит от правильности построения всего учебно-воспитательного процесса и от применения специфических приемов обучения.
Учащиеся коррекционных школ в силу их интеллектуальных особенностей лишены возможности изучения систематического курса геометрии.
Однако, при применении специфических приемов обучения, им вполне доступно усвоение элементарного геометрического материала.
В курсе 7 класса учащиеся заканчивают изучение геометрических фигур. Для лучшей систематизации знаний в конце года можно давать кодированные задания в режиме контроля (когда выполнение задания требует проверки с помощью учителя) и в режиме самоконтроля (управляемые задания), когда задания выполняются только правильно и никакой проверки не требуют, так как совершаемые ошибки исправляются в процессе выполнения задания.
Пример:
Тема задания:
«Свойства геометрических фигур»
Учащимися раздаются карточки с заданием и ответы под номерами.
Выбирая нужный ответ, учащиеся в карточку проставляют нужный номер
ответа.
|
Вопросы |
1 |
2 |
3 |
4 |
5 | |
|
|
Ответы | |||||
|
| ||||||
|
| ||||||
|
|
Вопросы;
1. Как называется фигура?
2. Все ли стороны равны?
3. Противоположные стороны попарно параллельны?
4. Диагонали равны?
5. Все ли углы равны 90 градусов?
ОТВЕТЫ:
|
На 1 вопрос: куб — 1 прямоугольник — 2 параллелограмм — 3 ромб — 4 |
На 3 вопрос: да — 1 нет — 2 |
|
На 4 вопрос: да — 1 нет — 2 | |
|
На 2 вопрос: да — 1 нет — 2 |
На 5 вопрос: да — 1 нет — 2 |
В курсе математики коррекционных школ центральной темой является нумерация целых неотрицательных чисел и действия над ними.
В каждом классе с небольшой долей усложненности звучит эта тема.
Однако учителю не всегда удается добиться должного навыка в счете и возникновения у детей абстрактного представления о числе.
Если в начальной школе можно применять счетный материал, то в старших классах лучше всего помогают карточки и следующее их решение.
Например:
Разложить числа 364 и 8702 на разрядные единицы. Учащиеся для лучшего понимания можно предложить следующее расположение чисел:
|
300 |
8000 |
|
60 |
700 |
|
4 |
2 |
Мысленно поставив «плюс», дети поймут, какое число в результате получается, более слабые учащиеся могут сделать сложение в столбик. Если учащиеся выполняют задание, в котором, например, требуется получить число 7003, то надо на число 7000 наложить 3. Все это требует сочетания двигательной и мыслительной активности, что способствует вовлечению учащихся в активный познавательный процесс.
Многие математические задания требуют выполнения ряда последовательных умственных действий. Но дети с пониженным интеллектом не всегда могут запомнить ряд действий, поэтому нужно промежуточное фиксирование.
Например: округлить число 7352 до сотен.
Порядок действий таков:
- выделить в числе разряды сотен и десятков;
- дать оценку количеству единиц в разряде десятков (1,2,3,4 или 5,6,7,8,9);
- отбросить в числе 2 последних знака, заменив их нулями;
- записываем полученное число, предварительно увеличив число единиц в разряде сотен (подписываем со знаком «+» 0 или 1)
73|52 ≈7400
+ 1
84|23 ≈8400
+ 0
Такой алгоритм под силу даже слабым учащимся и запоминается гораздо лучше.
Еще один пример: округление до тысяч можно рекомендовать следующее: учащийся должен отделить чертой (или обвести кружочком) разряд тысяч в числе. Этот условный знак поможет оценить количество единиц в разряде десятков, кроме того будет выделен и разряд, находящийся слева от десятков.
5|689≈6000
+ 1
6|277≈6000
+ 0
При прохождении материала «Обыкновенные дроби» учащиеся сталкиваются с рядом трудностей.
Так, алгоритм обращения смешанного числа в неправильную дробь, несмотря на его простоту, труден для запоминания. Опять приходит на помощь промежуточное фиксирование.
Например:
При превращении смешанного числа в неправильную дробь лучше поставить знаки между целыми числами и дробью, таким образом учащиеся сразу видят, какие действия производить:
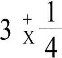
Большинство учащихся запоминают только сам алгоритм обращения. При сложении и вычитании обыкновенных дробей на начальном этапе можно применять следующие приемы:
Например:
![]()
1. взять разноцветные мелки (для доски) и карандаши (для тетрадей);
2. обводим кружком одного цвета целые числа;
3. обводим кружком другого цвета числителем;
т. е. школьники запоминают, что сначала складываем одноцветные
числители, а знаменатели остаются без изменения.
В результате этот прием перевода мысленного действия во внешние придает операции конкретный материальный характер, чем облегчает ее выполнение.
Анализируя задание, иногда требуется определить, какой из известных алгоритмов решения в данном случае необходимо применить. Примером такого случая может служить сокращения дробей. Необходимо предварительная работа. В результате, подходя к самому сокращению дробей трудно подобрать наибольшее число, на которое делится и числитель и знаменатель. Часто дети забывают разделить или числитель, или знаменатель. Опять помогает промежуточное фиксирование.
Например:
![]()
4 наибольший общий делитель 4 и 12.
Предлагается карандашом записать 4 рядом с числителем и знаменателем ипроизвести действие:
![]()
![]()
В задачи учителя математики коррекционной школы входит не только обучение вычислительным приемам, но и развитие логического мышления. Учитель добьется осознанного подхода со стороны ученика к решению примера или задачи, если в определенный момент задаст ему нетрадиционный вопрос.
При изучении порядка действий учащиеся часто не могут осознать значение скобок.
Например:
52 + 68•2 и (52+68)•2
Для четкого разграничения можно предложить следующий ряд вопросов:
– увеличить в 2 раза сумму 52 и 68;
– увеличить в 2 раза число 68 и сложить с числом 52;
– сравнить эти 2 суммы.
После сравнения дети уже самостоятельно могут сделать вывод о значении скобок.
Фиксирование промежуточных результатов в ходе выполнения задания помогает обучающимся с интеллектуальной недостаточностью.
Так, даже учащиеся с малыми математическими способностями лучше справляются с действиями с числами, полученными при измерении, если сопровождают операцию раздробления записью.
17 ц 98 кг • 17 =
100 кг • 17 = 1700 кг
1700 кг+98 кг = 1798 кг
Опыт убеждает, что действенной помощью учащимся будет рекомендация пользоваться в ходе выполнения задания записями или символическими знаками.
Часто возникают трудности при умножении и делении десятичных дробей на 10, 100 и 1000. Само правило легко заучивается учащимися, но при выполнении зачастую запятую ставят не там, например 10,2: 100= получают 1,02 вместо 0,102.
Или 0,9 • 1000 ученик делает ошибку в подсчете знаков, так как необходимого количества знаков множимое не имеет, их нужно приписать мысленно.
Если учитель предложит учащимся приписывать недостающие нули карандашом, а затем подсчитать все знаки между старой запятой и новой запятой, поставленной карандашом, то ошибок будет меньше.
0,070 ·1000 =
0,01:10 =
При делении чисел учителю следует потребовать от учащихся, прежде чем они приступят к решению, отделить галочкой в делимом первую группу цифр, которые составят число больше делителя; над каждым последующим знаком поставить точку и таким образом подсчитав знаки частного поставить на месте частного столько точек, сколько в нем будет знаков.
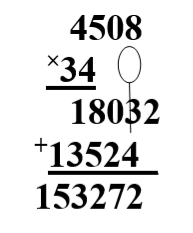
При умножении на двухзначное число, умножая на десятки, учащиеся теряются, где подписывать второе неполное произведение.
Можно предложить детям обвести цифру 3 карандашом и вниз провести стрелку, где подписывать.
Устный счет — обязательный элемент на уроке математики. В развитии способности мыслить и создании интереса к учению большое значение имеет такой материал, как задачи-смекалки, арифметические и геометрические головоломки. Для активизации мыслительной деятельности можно включить в урок следующие задания буквально на 5–7 минут.
Найди два числа
Обрати внимание на эту таблицу:
|
Числа, сумму которых составляет 7:Произведение этих чисел: |
1,6 6 |
2,5 10 |
3,4 12 |
|
Числа, сумму которых составляет 10:Произведение этих чисел: |
Нарисуй такую же таблицу и заполни ее всеми возможными решениями следующих примеров.
Найди два числа, у которых:
- Сумма равна 7 и произведение 10
- Сумма равна 7 и произведение 12
- Сумма равна 10 и произведение 16
- Сумма равна 10 и произведение 21
- Сумма равна 10 и произведение 9
- Сумма равна 9 и произведение 14
- Сумма равна 9 и произведение 20
- Сумма равна 9 и произведение 8
- Сумма равна 7 и разность равна 1
- Сумма равна 7 и разность равна 3
- Сумма равна 8 и разность равна 6
- Сумма равна 8 и разность равна 2
Какие два числа?
1, 2, 3... — это целые числа,
ВопросКакие два целых числа надо сложить друг с другом для того, чтобы получить в сумме 8?
Ответ: 1 и 7; 2 и 6; 3 и 5; 4 и 4,
Мы видим, что здесь существует 4 возможных решения. Можешь ли ты перечислить все возможные решения для примеров, расположенных внизу?
Помни: необходимо работать по определенной системе.
1 Какие два целых числа дают в сумме:
(а)5?
(б)6?
(в) 10?
(г) 12? (д) 15?
2 Какие два целых числа, умноженные друг на друга, дают в произведении:
(а)6?
(б)12?
(в)16?
(г)20?
(д)24?
3 Какие два целых числа до 15 при вычитании
друг из друга дают разность:
(а) 3?
(б) 6?
(в) 10?
(г) 11?
Разорванные прямоугольники
На разлинованном в клетку листе бумаги Маша нарисовала восемь разных прямоугольников. Потом эта бумага нечаянно была порвана. Попытайся определить, из скольких клеток состоял первоначально каждый прямоугольник?
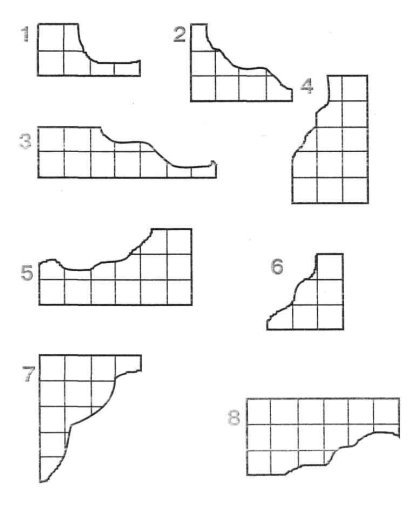
Найди два числа
Нарисуй такую же таблицу:
|
Первое число |
Второе число |
Сумма |
Найди два числа если:
- Их сумма равна 5 и одно из них на 1 больше другого
- Их сумма равна 8 и одно из них на 2 больше другого
- Их сумма равна 8 и одно из них на 4 больше другого
- Их сумма равна 12 и одно из них на 2 больше другого
- Их сумма равна 11 и одно из них на 1 больше другого
- Их сумма равна 15 и одно из них на 1 больше другого
- Их сумма равна 15 и одно из них на 3 больше другого
- Их сумма равна 9 и одно из них в два раза больше другого
- Их сумма равна 18 и одно из них в два раза больше другого
- Их сумма равна 30 и одно из них в два раза больше другого
- Их сумма равна 21 и одно из них s два раза больше другого
- Их сумма равна 27 и одно из них в два раза больше другого
Литература:
- В. В. Эк «Опыт использования условных обозначений на уроках математики во вспомогательной школе» журнал «Дефектология» № 2 1979 г. Москва изд. «Педагогика»
- «Логическая математика для младших школьников» Москва «Поматур» 1998г.

