In mathematics, the Cesàro means of a sequence 
are the terms of the sequence 
, where
is the arithmetic mean of the first n elements of 
.
This concept is named after Ernesto Cesàro (1859–1905).
A basic result states that the limit of a convergent sequence equals the limit of its Cesàro mean. That is, the operation of talking Cesàro means preserves the convergence and the limit of a sequence. This is the basis for using Cesàro means in summability method in the theory of divirgent series.
Let m space of really limited sequences with norm 
where 
. It is known that, m is a complete bordered space. We denote by 
the space of convergent sequence. It is obvious that, 
is a closed sub-space in 
. Next, we denote by 
the subset of 
consisting of sequence of convergent in Cesàro mean, i.e
if, exist limit 
, where 
Let the operator ch Cesàro be the operator associated with the 
sequence 
. We denote by 
set of sequence of 
, for which 
it is easy to notice that, 
Let 
Statement 1
All 
are a linear subspace of 
Task 1
Whether 
closed subspace when 
?
We consider sequences of m, such that 
or 1
Task 2
Does 
conformity m?
Definition 1. Let us given the sequence 
. If the sequence 
which consist of elements of the sequence 
converges to 
then the sequence 
converges to 
in Cesàro mean.
Example. Let us consider the following sequence
We have an oscillating sequence, but in the Cesàro means it has limit 
So, the sequence 
converges to 
in Cesàro mean.
Suppose given the sequence
such that
Where 
are terms of arithmetic progression.
Theorem 1. If 
are the terms of arithmetic progression, where 
and 
then sequence (1) is convergent in Cesàro mean.
Proof. 
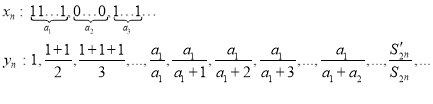
Where 
sum of odd members of arithmetic progression,
sum of all members of arithmetic progression.
Then sequence (1) is convergent in Cesàro mean to 
.
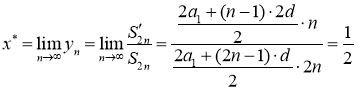
Theorem 2. If 
are terms of geometric progression, where 
and 
when
then sequence 
is not convergent in Cesàro mean.
Proof.
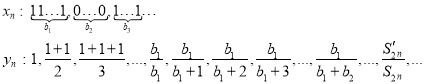
Where sum of odd members of geometric progression,
sum of all members of geometric progression.
then sequence is not convergent in Cesàro mean
.
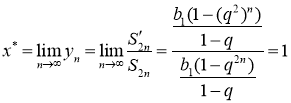Definition 2. Let us given the sequence 
. The sequences 
and 
whose consist of elements of the sequences 
and 
accordingly. If the second sequence 
converges to 
then the sequence 
has the second convergence to 
in Cesàro mean.
Theorem 3. If 
are the terms of geometric progression, where 
and 
Then the sequence (2) has the second convergence in Cesàro mean.
Proof.
Suppose given the sequence such that
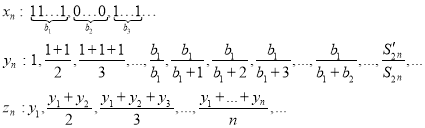
Where sum of odd members of geometric progression,
sum of all members of geometric progression.
Then sequence (2) is convergent in Cesàro mean to 
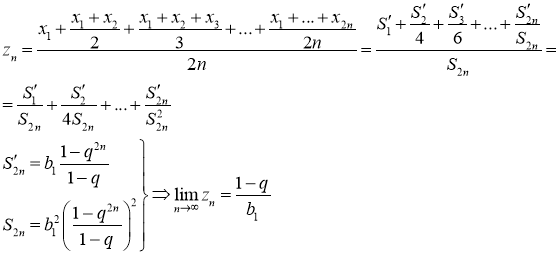
References:
- Hardy, G.H.(1992). Divergent Series. Providence: American Mathematical Society. ISBN 978–0-8218–2649–2
- Katznelson, Yitzhak (1976). An Introduction to Harmonic Analysis. New York: Dover publications. ISBN 978–0-486–63331–2
