Математическая модель функционирования щитовидной железы



Разработана математическая модель функционирования щитовидной железы, представляющая собой задачу Коши для системы обыкновенных дифференциальных уравнений. Учитываются основные биохимические реакции, протекающие в щитовидной железе: поступление йода, связывание его с тиреоглобулином, образование тироксина. Стационарные точки исследуются на устойчивость. Анализируются возможные стратегии лечения при нарушении функций щитовидной железы. Модель основана на принципе парных взаимодействий, балансных соотношениях и кинетике ферментативных реакций.

Ключевые слова: математическое моделирование, дифференциальные уравнения, щитовидная железа, ферментативная реакция.

Введение. Щитовидная железа играет важнейшую роль в организме млекопитающих, являясь частью сложной эндокринной системы. Эндокринная система вырабатывает биологически активные вещества — гормоны, осуществляющие регуляцию обмена веществ в организме, работы сердечно-сосудистой системы и центральной нервной системы. Заболевания эндокринной системы отражаются на работе как отдельных органов организма, так и всего организма в целом. Нормальное функционирование организма млекопитающих во многом зависит от устойчивой работы щитовидной железы. В ней перерабатывается поступающий в организм йод, и вырабатываются гормоны, регулирующие различные биохимические реакции. Синтез и освобождение гормонов включают в себя большой каскад биохимических реакций. Нарушение работы щитообразной железы на любом из уровней секреции гормонов, поступления йода в функциональное пространство, регулирования передачи гормонов в кровеносное русло может привести к различным заболеваниям [4, 9, 15].

Математические модели различных органов живых организмов позволяют выявить наиболее значимые их функции, оценить наиболее опасные нарушения в работе, выработать стратегию лечения. В научных публикациях значительное внимание уделено построению моделей йодного обмена в организме и математическим моделям эндокринной системы [6, 11–14], в которых учитываются в некоторой степени и функции щитовидной железы. Математическая модель фолликула железы, в которой учитываются основные биохимические реакции, протекающие в нем: поступление йода, связывание его с тиреоглобулином с последующим образованием и накоплением гормона , разработана в [1, 3]. Модель представлена задачей Коши для системы трех обыкновенных дифференциальных уравнений. Ниже предлагается математическая модель, отличная от разработанной в [1] модели.

Основные биохимические реакции. Функциональной единицей щитовидной железы является шарообразный фолликул, состоящий из фолликулярных клеток (тироцитов) [8, 9, 14], которые окружают коллоид. В фолликулярные клетки нагнетается йод (I), который под действием ферментов активизируется, затем из фолликулярных клеток поступает в коллоид. В коллоиде в результате связывания йода с тиреоглобулином (Tg), образуются тиреоидные гормоны, 95 % из которых составляет гормон тироксин (Т4). Гормоны хранятся в коллоиде в связанном с тиреоглобулином виде. При снижении уровня тиреоидных гормонов в сыворотке крови гормоны отщепляются от тиреоглобулина и из фолликулярной клетки в свободном виде попадают в кровоток, где и выполняют свои регуляторные функции [16].

Недостаток йода в организме вызывает и недостаток гормона T4, а избыток йода — избыток гормона. В обоих случаях реакцией организма на изменение количества вырабатываемого гормона может являться команда на увеличении объема щитовидной железы в первом случае направленное на увеличение выхода гормона T4, а во втором на — необходимость переработать избыточный йод. Нарушение функций щитовидной железы может привести к возникновению различных заболеваний в организме и образованию различных типов новообразований в самой железе [15]. Для восстановления функций щитовидной железы в клинической практике, как правило, используется терапевтические методы лечения.

Математическая модель щитовидной железы. Щитовидная железа представляет собой объединение многочисленных фолликул разного размера [5, 8], одинаково функционирующих. То есть, коллоид и окружающие его фолликулярные клетки можно считать равномерно распределенными по всему пространству, занимаемому щитовидной железой. Поэтому в математической модели железа представлена объединением коллоида и фолликул. Учитываются основные процессы, происходящие в железе: поступление внешнего активного йода, присоединение йода к тиреоглобулину, образование гормона Т4, его связывание с тиреоглобулином и высвобождение гормона Т4 через внешнюю оболочку железы [9]. Тиреоглобулин сохраняется в железе, во внешнюю среду не поступает. Основная доля секретируемого гормона приходится на Т4, поэтому в модели рассматривается именно его синтез. Предполагается, что среда, в которой происходят реакции, является гомогенной. При построении математической модели использовались подходы, аналогичные примененным в [10].

Пусть — концентрация активного йода в железе, — концентрация тиреоглобулина, — концентрация гормона Т4. Предполагается, что скорости реакций связывания йода и тиреоглобулина, а также тиреоглобулина и гормона пропорциональны их концентрациям: скорость образования тиреоглобулина пропорциональна концентрации йода, а скорость образования гормона пропорциональна концентрации тиреоглобулина. При этих предположениях первая реакция описывается функций , а вторая — . С учетом введенных обозначений и гипотез о реакциях, система дифференциальных уравнений, описывающая процессы, происходящие в щитовидной железе, имеет следующий вид:

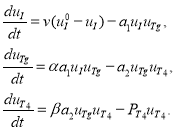(1)

В этих уравнениях — проницаемость внешней мембраны железы, — скорость поступления йода в железу, — равновесная концентрация йода в случае отсутствия реакций, , , , — положительные константы, характеризующие скорости реакций.

Первое уравнение в (1) описывает скорость изменения концентрации йода: поступление йода в коллоид и выход его остатков (слагаемое ) и скорость связывания йода с тиреоглобулином (слагаемое ). При этом считается, что йод уже находится в активном состоянии. Второе уравнение в (1) описывает скорость изменения концентрации тиреоглобулина: слагаемое — скорость образования тиреоглобулина, слагаемое — скорость связывания тиреоглобулина с гормоном Т4. Третье уравнение в (1) описывает процесс образования тиреоидного гормона Т4: слагаемое — скорость образования гормона Т4, слагаемое — скорость выхода гормона Т4 через внешнюю мембрану железы в кровяное русло.

Анализ стационарных состояний системы. Система уравнений (1) имеет стационарную точку , . Одно из трех собственных значений , , матрицы Якоби правой части системы уравнений (1) в этой стационарной точке положительно, и, соответственно, эта точка будет неустойчивой. Неустойчивость этого положения равновесия рассматривается как начало естественного функционирования щитовидной железы [1–3].

Система уравнений (1) содержит еще одну стационарную точку, являющиеся решением системы реккурентных уравнений

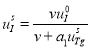, , (2)

Характеристический полином

матрицы Якоби правой части уравнений (1) в этой стационарной точке согласно критерия Гурвица и теоремы Бюдана-Фурье имеет одно отрицательное собственное значение и два либо отрицательных, либо комплексно сопряженных с отрицательными вещественными частями. Поэтому эта стационарная точка является устойчивой.

С учетом опубликованных в литературных источниках относительных значений констант [1, 7, 9] в модели можно принять — , . Остальные константы выбираются из условий обеспечения заданных выходных характеристик на основании соотношений (2): конверсия йода составляет 90 %, а на выходе отношение концентрации гормона к концентрации тиреоглобулина равно 4:1 [1]. За единичную принимается константа . С учетом этого, в модели принято: , , , , , , . При принятом наборе констант единица измерения времени в модели соответствует 30 суткам, а концентрации веществ считаются безразмерными. При этом принимается, что в стационарном («базовом») состоянии

, , . (3)

Эта стационарная точка рассматривается как «естественное» положение равновесия, а отклонение от него считается нарушением функции щитовидной железы.

На рис. 1 отражена зависимость мнимой части пары комплексно сопряженных собственных значений правой части уравнений (1) и минимальной по модулю вещественной части в стационарных точках от параметра . Символом * на рис. 1 отмечены значения этих величин в «базовой» точке. Как следует из анализа полученных результатов увеличение одного из параметров , , или сопровождается увеличением частоты колебаний в окрестности стационарных точек и увеличением абсолютной величины действительной части собственных значений в окрестности стационарных точек (рис. 1).

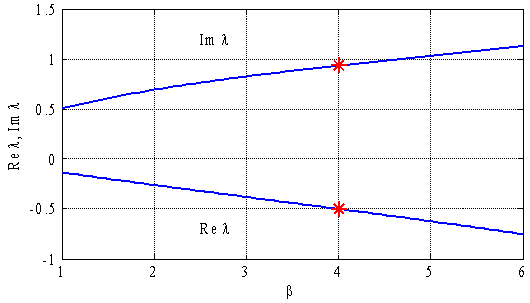
Рис. 1.

Нарушение функций щитовидной железы

К внутренним факторам, связанных с нарушением функций щитовидной железы, относятся изменение механических свойств внешней мембраны, изменение скоростей протекающих реакций, недостаточное или избыточное поступление в организм йода, необходимого для нормальной выработки гормонов. Под нарушением функций щитовидной железы в модели (1) понимается отклонение значений постоянных, , , , , , и значения от значений, при которых реализуется заданное стационарное состояние (3).

Лечение заболеваний щитовидной железы в клинической практике осуществляется введением в организм или в щитовидную железу химических препаратов, позволяющих ликвидировать возникшие нарушения [9]. Лечение начинается спустя некоторое время после его возникновения, поскольку оно обнаруживается после превышения биохимических показателей некоторых пороговых значений. Под восстановлением функций щитовидной железы понимается программа уменьшения возмущений до значений, при которых основные биохимические показатели не будут выходить за пороговые значения.

Пусть — возмущение, которое получает один из параметров , , , , или в момент времени . Система, поскольку все стационарные точки устойчивые, начинает переход в ново устойчивое стационарное состояние. Лечение начинается в момент времени . В модели принимается, что скорость восстановления возмущенного параметра пропорциональна величине возмущения и концентрации препаратов . Тогда уравнение восстановления функции принимает вид

,(4)

где — программа введения препаратов. Это уравнение совместно с системой уравнений (1) будет моделью восстановления функций. Ведение препаратов осуществляется до тех пор, пока возмущение не станет меньше заданной величины. То есть, если выполнится условие , где — значение возмущенного параметра в естественном состоянии.

Для случая возмущения параметра система уравнений (1) совместно с (4) представляет собой модель восстановления нормального протекания реакции связывания тиреоглобулина и гормона :

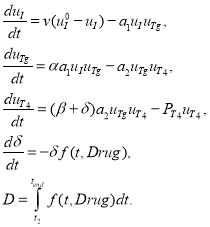(5)

В этой системе уравнений — момент времени начала лечения, а — окончания, — количество препаратов, израсходованных на лечение.

Рассматриваются две стратегии лечения. Пусть в момент времени возникло нарушение, а лечение начинается в момент времени . Введение препаратов можно осуществлять постоянно или периодически.

Первый вариант. Введение препаратов начинается в момент времени и заканчивается, если выполнится условие :

если или , то;

если и , то ,

где заданная малая величина.

На рис. 2 для случая , , отражено изменение во времени для и . Символом «о» отмечены моменты времени, когда выполняется неравенство . Вертикальной пунктирной линией отмечено время начала лечения. Зависимость времени лечения от значений отражена на рис. 3. Расход препаратов в обоих случаях отличается незначительно.

Второй вариант. Ввод препаратов осуществляется периодически. Выбран вариант, когда на практике реализуются несколько курсов лечения через определенные промежутки времени:

если или , то;

если и , то

, если

и

, если .

На рис. 4 приведены результаты решения уравнений (5) для случая и в виде зависимости . Программе введения препаратов соответствует кривая .

Аналогичные результаты получены и для параметров , , , .

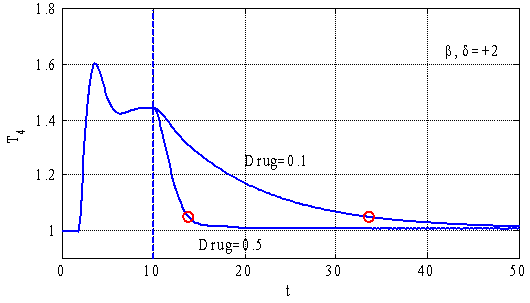
Рис. 2.

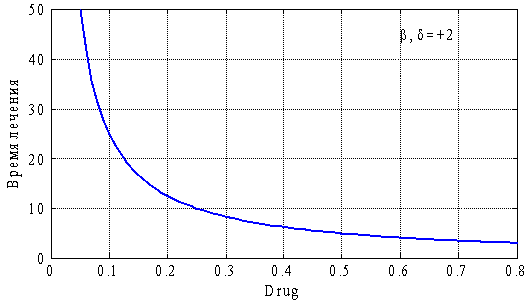
Рис. 3.

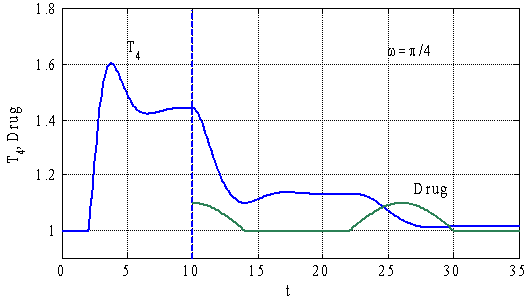
Рис. 4.

Как следует из анализа полученных результатов, общее количество препаратов, обеспечивающих уменьшение возмущения параметра до заданного уровня, во всех трех рассмотренных случаях отличаются незначительно и равно . То есть в математической модели (5) программа восстановления функций не является чувствительной к расходу препаратов. Их затраченное количество влияет только на время лечения.

Литература:

1. Балыкина Ю. Е., Колпак Е. П Математические модели функционирования фолликула щитовидной железы // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2013. — № 3. — С. 20–31.
2. Колпак Е. П., Балыкина Ю. Е., Котина Е. Д., Жукова И. В. Математическая модель нарушений функционирования щитовидной железы // Молодой Ученый. — 2014. — № 2(61). — С. 19–24.
3. Balykina Ju.E., Kolpak E. P., Kotina E. D. Mathematical Model of Thyroid Function // Middle-East Journal of Scientific Research. — 2014. — V. 19. — no. 3. — PP. 429–433.
4. Carpi A., Mechanick J. I. Thyroid Cancer from Emergent Biotechnologies to Clinical Practice Guidelines. CRC Press Taylor & Francis Group. London, New York. 2011. 382 p.
5. Danziger L., Elmergreen G. L. The thyroid-pituitary homeostatic mechanism // The bulletin of mathematical biophysics. — 1956. — V. 18. — no. 1. — PP. 1–13.
6. Degon M, Chipkin S. R., Hollot C. V., Zoeller R. T., Chait Y. A computational model of the human thyroid // Math. Biosci. — 2008. — V. 212. — no. 1. — PP. 22–53.
7. Distefano J. J., Mak P. H. Optimal control policies for the prescription of thyroid hormones // Math. Biosci. — 1978. — V. 42. — no. 3–4. — PP. 159–186.
8. Gesing A., Bartke A. Decreased thyroid follicle size in dwarf mice may suggest the role of growth hormone signaling in thyroid growth regulation // Thyroid Research. — 2012. — V. 5. — no. 1. — PP. — 7.
9. Kettyle W. M., Arky R. A. Endocrine path physiology. New York. Lippincott — Raven. — 1998. 336 p.
10. Kolpak E. P., Kabrits S. A., Bubalo V. The follicle function and thyroid gland cancer // Biology and Medicine. — 2015. — Т. 7 (1). — BM060.15.
11. Lamooki G. R. R., Shirazi A. H., Mani A. R. Dynamical model for thyroid // Commun Nonlinear Sci Numer Simulat. — 2015. — V. 22. — pp. 297–313.
12. Leow M. K. S. A mathematical model of pituitary-thyroid interaction to provide an insight into the nature of the thyrotropin-thyroid hormone relationship // Journal of Theoretical Biology. — 2007. — V. 248. — no. 2. — PP. 275–287.
13. Mukhopadhyay B., Bhattacharyya R. A mathematical model describing the thyroid-pituitary axis with time delays in hormone transportation // Applications of mathematics. — 2006. — V. 51. — no. 6. — pp. 549–564.
14. Rupik W. Structural and ultrastructural differentiation of the thyroid gland during embryogenesis in the grass snake Natrix natrix L. (Lepidosauria, Serpentes) // Zoology. — 2011. — v. 114. — pp. 284– 297.
15. Takano T. Fetal cell carcinogenesis of the thyroid: Theory and practice // Seminars in Cancer Biology. — 2007. — V. 17. — no. 3. — P. 233–240.
16. Toda S., Koike N., Sugihara H. Thyrocyte integration, and thyroid folliculogenesis and tissue regeneration: perspective for thyroid tissue engineering // Pathology International. — 2001. — V. 51. — no. — 6. — PP. 403–417.