Данная статья посвящена особенностям расчёта пологих железобетонных сводов, опирающихся на металлические балки. В ней приведены основные причины ошибок при проектировании подобных конструкций, ведущие, в дальнейшем, к их неоправданному усилению.
Кроме того, разработана новая методика расчёта конструкции, учитывающая совместную работу её элементов. Данный метод использован в расчёте надподвального перекрытия Дома Мельникова в Санкт-Петербурге. Результаты расчёта сравнены со значениями, полученными в результате инструментального анализа.
Ключевые слова: железобетонные своды, расчёт, совместная работа, перекрытие.
Введение
В конце XIX — начале XX вв. одним из конструктивных решений междуэтажных перекрытий в зданиях было перекрытие по металлическим балкам. Межбалочные заполнения могли быть различными — из кирпичных, бетонных или железобетонных сводов, из плоских кирпиче-железных покрытий, с использованием волнистого железа или гипсовых досок. Самым распространённым среди них являлось перекрытие с накатом в виде бетонных сводиков.
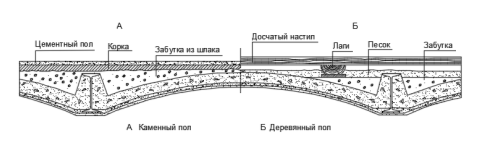
Рис. 1. Междуэтажное перекрытие по металлическим балкам
Высокая степень огнестойкости, коррозионная стойкость, а также дешевизна железа и цемента и простота их изготовления способствовали массовому внедрению данной конструкции в строительство гражданских зданий, а способность выдерживать значительные нагрузки — в строительство некоторых фабричных и промышленных зданий.
Подобные конструкции перекрытий использовались недолго и перестали применяться уже в первой трети XX века. В основном, это произошло из-за активного использования в строительстве железобетонных конструкций.
Несмотря на то, что перекрытия по металлическим балкам с накатом в виде бетонных сводиков применялись сравнительно недолго, зданий с подобным конструктивным решением сохранилось немало.
Многие из таких перекрытий по результатам визуального осмотра и поверочного расчёта находятся в неудовлетворительном состоянии и нуждаются в ремонте, усилении или замене конструкций. Несмотря на это, они продолжают воспринимать приложенные к ним нагрузки.
Этот факт говорит о том, что в настоящее время нет достоверных методик расчёта перекрытий со сводчатым заполнением. Рассмотрим основные причины их отсутствия.
Основные причины отсутствия достоверных методик расчёта
Из всех факторов, приводящих к неверным расчётам рассматриваемых перекрытий, можно выделить два основных:
- Ошибочный анализ напряжённо-деформированного состояния конструкции перекрытия.
Период с середины XIX в. характеризовался активным изучением арочно-сводчатых конструкций. Основная часть исследований в то время была ориентирована на расчёт исключительно каменных сводов, преимущественно полуциркульных или лучковых ![]() .
.
Появление в конце столетия плоских бетонных сводчатых конструкций не вызвало должного научного интереса. Учёных волновал, в основном, бетон как строительный материал, так как на тот момент он ещё не был достаточно изучен. Характер работы самой конструкции детально не исследовался. С учётом того, что подъём свода составлял всего от 1/6 до 1/12 от пролёта, его геометрией пренебрегали, рассматривая конструкцию как обычную балку. Подтверждение этому можно найти во многих научных работах того времени. Например, в книге В. Р. Бернгарда «Арки и своды. Руководство к устройству и расчёту арочных и сводчатых перекрытий», 1901 г., сказано следующее: «Конструкция плоских сводов на металлических балках относится к балочным перекрытиям, и здесь не подлежит рассмотрению».
Точно такой же подход используется и при современных поверочных расчётах. Между тем, он совершенно недопустим. Своды, даже плоские, имеют горизонтальные реакции распора, которые отсутствуют в балках. Такой некорректный анализ напряжённо-деформированного состояния конструкции и приводит в дальнейшем к ошибкам в расчётах.
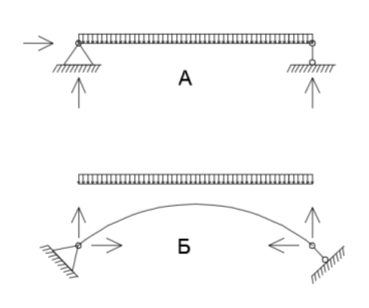
Рис. 2. Опорные реакции: А — в балке, Б — в своде
- Отсутствие необходимости в расчёте конструкции перекрытия.
При строительстве зданий были нередки случаи, когда расчёт конструкций перекрытий не проводился. Объяснялось это тем, что учёные опирались на накопленный опыт и брали конструкции «на глаз», с большим запасом прочности. Кроме того, при необходимости они могли жёстко зафиксировать концы балок в стене, тем самым заметно уменьшить прогиб и увеличить прочность конструкции.
Между тем, такие ошибки при расчётах приводят к сильно заниженным результатам, и, как следствие, к неоправданному усилению конструкций и перерасходу материала. Таким образом, возникает необходимость в совершенствовании методов расчёта сводчатых перекрытий.
Эта цель может быть достигнута путём приведения конструкции перекрытия к комбинированной конструкции, в которой металлические балки будут работать совместно с бетонными сводами.
Расчёт надподвального перекрытия Дома Мельникова вСанкт-Петербурге
В 2017 г. Институтом проектирования и обследования строительных конструкций, зданий и сооружений Санкт-Петербургского государственного архитектурно-строительного университета была выполнена оценка технического состояния несущих конструкций надподвального перекрытия Дома Мельникова, расположенного по адресу: Сапёрный пер., д.10, лит. Б.

Рис. 3. Надподвальное перекрытие. Фрагмент
Данные конструкции состояли из бетонных сводов, опёртых на металлические балки. Сечение балок — I № 25 немецкого сортамента [4], пролёт — 7,8 м.
По данным инструментального анализа прогиб балки составил 3,0 см.

Рис. 4. Надподвальное перекрытие. Фрагмент
Произведём аналитический расчёт данного надподвального перекрытия.
Проверяем наиболее нагруженный участок перекрытия. Несущими элементами перекрытия являются металлические балки I№ 25 немецкого сортамента [4] (Ix=4966 см4, Wx=397 см3, Aб=49,7 см2, Pn=39 кг/м) и работающие совместно с ними бетонные своды. Расстояние между балками a=1,5 м.
Расчётный пролёт балки l0 принимаем равным
![]() (1)
(1)
где l — длина балки, м; l’ — величина заделки балки в кирпичную стену, м.
![]()
Производим сбор нагрузок на балку перекрытия (см. Табл. 1).
Таблица 1
Сбор нагрузок на балку перекрытия
|
№п/п |
Наименование |
Нормативная нагрузка, кг/м |
Коэффициент надёжности по нагрузке |
Нормативная нагрузка, кг/м |
|
Постоянная | ||||
|
1 |
Собственный вес металлической двутавровой балки, I25 немецкого сортамента |
39,0 |
1,05 |
41,0 |
|
2 |
Бетонные своды толщиной 85–100 мм, p=2300 кг/м3 |
345 |
1,3 |
448,5 |
|
3 |
Засыпка строительным мусором, 210–290 мм, p=1300 кг/м3 |
487,5 |
1,3 |
633,7 |
|
4 |
Цементно-песчаная стяжка, 20 мм, p=2300 кг/м3 |
69 |
1,3 |
89,7 |
|
5 |
Керамическая плитка, 10 мм, p=1800 кг/м3 |
18 |
1,1 |
19,8 |
|
gn= |
959 |
g= |
1232,7 | |
|
Временные | ||||
|
6 |
Полезная нагрузка на перекрытие |
200 |
1,2 |
240 |
|
qn= |
1159 |
q= |
1473 |
Определяем изгибающие моменты от расчётной и нормативной нагрузок по формулам (2), (3):
![]() (2)
(2)
![]() (3)
(3)
где q и qn — расчётная и нормативная нагрузки на балку, кг/м.
![]()
![]()
Определяем величину длительно действующей нагрузки на 1 м.п. балки перекрытия по формуле (4):
![]() (4)
(4)
где a — расстояние между балками, м; qr — пониженное нормативное значение нагрузки, кг/м2 [5]; ![]() – коэффициент надёжности по нагрузке [5].
– коэффициент надёжности по нагрузке [5].
![]()
Вычисляем величину распора, возникающего в сводах по формуле (5):
![]() (5)
(5)
где b — пролёт свода, м; f — стрела подъёма свода, м.
![]()
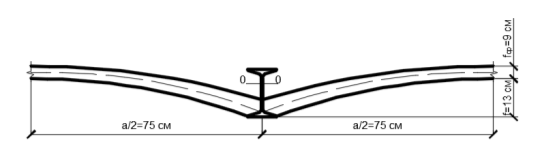
Рис. 5. Расчётное сечение
Определяем положение центра тяжести комплексного сечения по формуле (6):
![]() (6)
(6)
где ![]() — суммарный статический момент, приведённый к металлу,
— суммарный статический момент, приведённый к металлу, ![]() ;
;![]() — приведённая площадь сечения,
— приведённая площадь сечения, ![]() .
.
Для определения статического момента разбиваем участок свода на прямоугольники (19,25х9) см (рис.6). Статический момент определяем по формуле (7):
![]() (7)
(7)
где Fi — площадь i-ого участка свода, ![]() ; yi — расстояние от i-ого участка свода до оси Х, см.
; yi — расстояние от i-ого участка свода до оси Х, см.
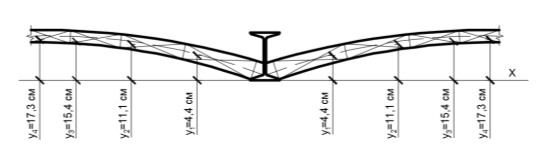
Рис. 6. Определение координат центра тяжести площадей относительно оси Х
![]()
Определяем статический момент балки относительно оси Х по формуле (8):
![]() (8)
(8)
где Aб — площадь сечения балки, см2; y — расстояние от центра тяжести балки до оси Х, см.
![]()
Определяем суммарный статический момент, приведённый к металлу по формуле (9):
![]() (9)
(9)
где m — отношение модулей упругости стали и бетона.
Для бетона класса В25
![]()
![]()
Определяем положение центра тяжести свода по формуле (10):
![]() (10)
(10)
где Aсв — площадь свода, ![]() .
.
![]()
Определяем приведённую площадь сечения по формуле (11):
![]() (11)
(11)
![]()
Определяем положение центра тяжести объединённого сечения
![]()
Определяем момент инерции приведённого сечения относительно нейтральной оси по формуле (12):
![]() (12)
(12)
где ![]() — момент инерции сечения балки относительно оси, проходящей через центр тяжести сечения балки, см4; y1 — положение центра тяжести объединённого сечения, см;
— момент инерции сечения балки относительно оси, проходящей через центр тяжести сечения балки, см4; y1 — положение центра тяжести объединённого сечения, см;![]() — момент инерции сечения свода относительно собственной центральной оси, см4; y2 — расстояние между центром тяжести объединённого сечения и центром тяжести свода, см.
— момент инерции сечения свода относительно собственной центральной оси, см4; y2 — расстояние между центром тяжести объединённого сечения и центром тяжести свода, см.
Момент инерции сечения свода относительно собственной оси определяется по формуле (13):
![]() (13)
(13)
где Fi — площадь i-ого участка свода, см2; yi — расстояние от центра тяжести объединённого сечения до i-ого участка свода, см.
![]()
Определяем момент инерции приведённого сечения
![]()
Определяем моменты сопротивления для верхней и нижней граней балки по формулам (14), (15):
![]() (14)
(14)
![]() (15)
(15)
гдe yв — расстояние от центра тяжести объединённого сечения до верхней грани балки, см; yн — расстояние от центра тяжести объединённого сечения до нижней грани балки, см.
![]()
![]()
Определяем напряжения в расчётных точках балки и проводим проверку на прочность по первой группе предельных состояний по формулам (16), (17):
![]() (16)
(16)
![]() (17)
(17)
где ![]() и
и ![]() – напряжения в верхней и нижней расчётных точках балки, кг/см2; R=1682 — расчётное сопротивление стали балки, кг/см2.
– напряжения в верхней и нижней расчётных точках балки, кг/см2; R=1682 — расчётное сопротивление стали балки, кг/см2.
![]()
![]()
Прочность балки по первой группе предельных состояний обеспечена.
Определяем прогиб балки и проводим проверку по второй группе предельных состояний по формуле (18):
![]() (18)
(18)
где ![]() — допустимый прогиб балки, см;
— допустимый прогиб балки, см; ![]() - модуль упругости стали, кг/см2.
- модуль упругости стали, кг/см2.
![]()
![]()
![]()
Требование норм по второй группе предельных состояний выполняется.
Выводы
По результатам приведённого расчёта прогиб балок данной конструкции составил 3,14 см. Вычисленное значение прогиба практически совпадает с прогибом, полученным в результате инструментального анализа (3,0 см).
На основании полученных результатов можно сделать вывод о том, что данная методика расчёта решает главную проблему сводчатых перекрытий по металлическим балкам — учёт совместной работы их элементов.
В настоящее время такая методика является наиболее точной и при позволяет проектировать перекрытия без чрезмерного запаса прочности.
Литература:
- Лахтин Н. К. Расчёт арок и сводов. Руководство к аналитическому и графическому расчёту арочных и сводчатых перекрытий. М.: Студенческое издательское общество, 1911. 492 с.
- Житкевич Н. А. Графический расчёт цилиндрических сводов на основании теории упругости. СПб.: Типография и литография В. А. Тиханова, 1898. 146 с.
- Полещук А. А. Расчёт и кладка сводов. Литографированные записки. 1898.
- Рынин Н. А. Металлическое покрытие его расчет и конструкция с приложением таблиц для расчета металлических покрытий и чертежей некоторых деталей конструкции последних. СПб.: 1905.
- СП 20.13330–2011 «Нагрузки и воздействия». Актуализированная редакция СНиП 2.01.07.85*. М.: 2011.

