В работе рассматриваются вопросы, связанные с проверкой устойчивости внутренней структуры шкалы экстраверсии опросника NEO PI-R. Сообщается о построении оптимальных структурных моделей этой шкалы, которые получены при помощи многомерных статистических методов и численного ресамплинга.
Ключевые слова: NEO PI-R, психометрическая шкала, экстраверсия, численный ресамплинг, бутстреп, факторный анализ, анализ главных компонент, язык программирования R.
Построение оптимальных моделей в психологии, социологии, педагогике и других гуманитарных науках является важной и актуальной задачей, для решения которой необходимо уметь подробно исследовать свойства валидности тестов как инструмента измерения и уметь выделять статистически значимые и незначимые модели. Исследованиям психологических конструктов и опросников посвящено большое количество работ классиков психометрики и современных авторов. Однако, исследования оптимальных моделей психометрических шкал опросника NEO PI-R, насколько известно авторам, проведено не было.
Персональный опросник NEO PI-R был создан в середине 90-х годов прошлого века в результате развития концепции «Большая Пятерка» о пятифакторной модели личности [1, 2, 4, 5]. Удачная архитектура опросника предопределила его многочисленные научные и коммерческие приложения [4]. Имеется несколько русскоязычных версий опросника NEO PI-R. Для целей данной работы был использован вариант, подготовленный группой преподавателей и студентов РГГУ в рамках совместных российско-американских исследований [12, 19]. За минувшие семнадцать лет психометрические свойства русскоязычного варианта опросника NEO PI-R подробно исследованы. Результаты исследований опубликованы в цикле статей [19, 13, 8, 9, 16, 17] и нескольких дипломных работах, выполненных на кафедре фундаментальной и прикладной математики ИИНТБ РГГУ [6, 10, 18, 11, 7, 14].
В работе рассмотрены задачи, связанные с определением достаточного числа факторов для моделирования внутренней структуры психометрической шкалы E_Экстраверсия опросника NEO PI-R, исследована устойчивость внутренней структуры этой шкалы по отношению к малым изменениям имеющегося набора данных, и построены оптимальные факторные модели домена E_Экстраверсия. Для снижения размерности данных и анализа их внутренней структуры использовались многомерные статистические методы и численный ресамплинг [22, 21, 15, 20]. На языке программирования R разработаны программные средства для построения ансамблей факторных моделей с заданными свойствами.
Для определения числа факторов в процессе факторного анализа и количества главных компонент при редукции данных использовались известный критерий Кайзера-Харриса [15] и параллельный анализ [3]. Оба метода были усилены тем, что применялись для 1000 псевдовыборок, полученных из реальных данных при помощи классической бутсреп-процедуры с последующей проверкой статистических гипотез о количестве факторов и главных компонент. По усиленному критерию Кайзера-Харриса, дополненному критерием Стьюдента, статистически значимо предлагается выделить 3 фактора при построении факторных моделей и 2 главные компоненты при редукции данных. Тот же самый результат получен на основании параллельного анализа с симуляциями 20 случайных наборов данных параллельно каждой псевдовыборке.
Хотелось бы отметить, что относительные частоты трехфакторных и четырехфакторных моделей отличаются не слишком сильно и четырехфакторные модели необходимо рассматривать при исследовании устойчивости внутренней структуры данных. По усиленному критерию Кайзера-Харриса относительная частота всех трехфакторных моделей 0.55, а всех четырехфакторных моделей 0.45. Усиленный параллельный анализ показал, что относительная частота трехфакторных моделей 0.56, четырехфакторных моделей 0.42, и даже двухфакторные модели имеют ненулевую относительную частоту, равную 0.02.
Для каждой из 1000 псевдовыборок построена факторная модель с соответствующим количеством факторов. Все полученные модели сохранены в репозитории для дальнейшего исследования и применения. Из 1000 построенных факторных моделей сформированы ансамбли структурно различных моделей. Получилось 37 трехфакторных и 48 четырехфакторных моделей. Оптимальными факторными моделями признаны такие модели, которые встречаются значительно чаще остальных и имеют доминирующие относительные частоты. Такие модели требуют особого внимания и отдельного, не только компьютерного, исследования.
На Рис. 1 и 2 представлены конкурирующие и различные трехфакторные модели с относительными частотами 0.16 и 0.14 соответственно. Все другие трехфакторные модели имеют гораздо меньшие относительные частоты.
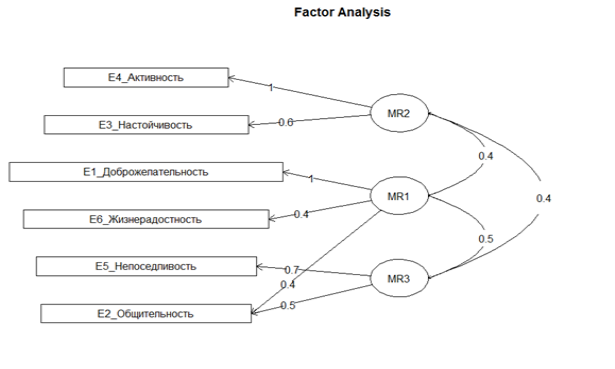
Рис. 1.Оптимальная трехфакторная модель шкалы E_Экстраверсия с относительной частотой 0.16.
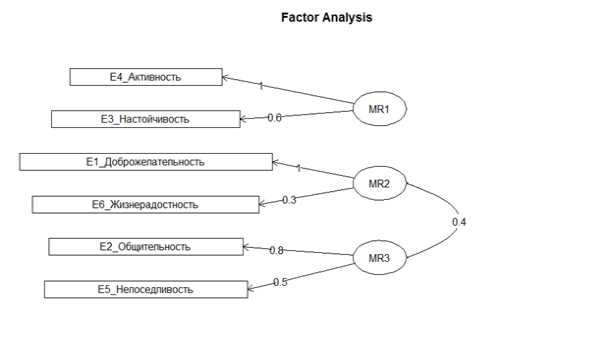
Рис. 2. Оптимальная трехфакторная модель шкалы E_Экстраверсия с относительной частотой 0.14.
На Рис. 3 приведена единственная доминирующая четырехфакторная модель. Важно отметить, что суммарный процент дисперсии данных, который объясняют доминирующие трех- и четырехфакторные модели, практически не различается и составляет приблизительно 58 %.
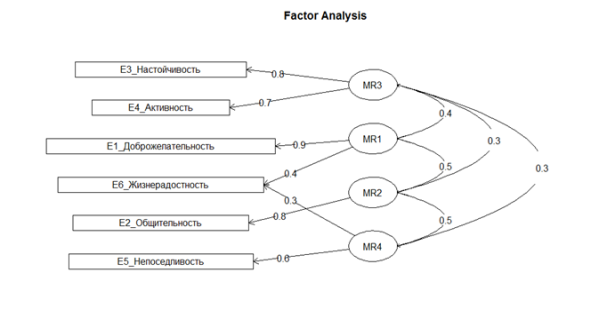
Рис. 3. Оптимальная четырехфакторная модель шкалы E_Экстраверсия с относительной частотой 0.13.
Таким образом, в данной работе при помощи многомерных статистических методов и численного ресамплинга были построены все оптимальные факторные модели психометрической шкалы E_Экстраверсия опросника NEO PI-R. При этом были разработаны специальные программные средства на языке программирования R для построения ансамблей факторных моделей и отбора статистически значимых и оптимальных факторных моделей. Разработанные программные средства будут полезны для конструирования новых психометрических инструментов и для исследования свойств существующих психометрических шкал.
Литература:
- Costa, P.T., Jr., & McCrae, R. R. Revised NEO Personality Inventory: Professional manual. Odessa, FL: Psychological Assessment Resources, 1992.
- Costa P. T. Jr., & Widiger T. A. Personality disorders and the five-factor model of personality. — Washington, DC: American Psychological Association, 1994.
- Humphreys L. G., Montanelli Jr R. G. An investigation of the parallel analysis criterion for determining the number of common factors //Multivariate Behavioral Research. — 1975. — Т. 10. — №. 2. — С. 193–205.
- Piedmont R. L. The Revised NEO Personality Inventory: Clinical and Research Applications. — New York, Boston. Dordrecht, London: Kluwer Academic / Plenum Publishers, 1998.
- Shmelyov A. G. & Pokhil'ko V. I. A taxonomy-oriented study of Russian personality-trait names // European Journal of Personality. — 1993. — № 7. — С. 1–17.
- Аверьянова М. М. Применение многомерных статистических методов для исследования данных анкетирования по тесту NEO PI-R: Дипл. раб. — М.: РГГУ, 2004.
- Башкиров Г. А. Исследование устойчивости внутренней структуры психометрических шкал опросника NEO PI-R при помощи многомерных статистических методов и численного ресамплинга: выпускная квалификационная работа. — М.: РГГУ, 2017.
- Боровиков Д. В., Синицын В. Ю. От психолексических исследований и пятифакторной модели личности к статистическому конструированию новых психометрических шкал // Математика и её приложения: Сборник трудов IV Международной научной конференции «Математика. Образование. Культура»: в 3-х ч. Ч. 1. 21–24 апреля 2009 г., Россия, г. Тольятти. — Тольятти: ТГУ, 2009. — С. 65–69.
- Боровиков Д. В., Синицын В. Ю. Применение пошаговых методов анализа надёжности для построения новых психометрических шкал // Обозрение прикладной и промышленной математики. — М., 2009. — Т. 16. — Вып. 3. — С. 455–456.
- Бутримова Н. Г. Статистический анализ надежности и оптимизация психометрических шкал теста NEO PI-R: Дипл. раб. — М.: РГГУ, 2004.
- Воробьев А. С. Разработка статистических методов построения новых психометрических шкал: выпускная квалификационная работа. — М.: РГГУ, 2016.
- Воронов А. Я., Зайчикова Е. А., Синицын В. Ю. Некоторые кросс-культурные психологические различия российских и американских студентов // Ценностная и социальная идентичность российской гуманитарной интеллигенции: Тезисы всероссийской теоретико-методологической конференции. Москва, 26–27 апреля 2000 г. — М.: РГГУ, 2000. — С. 120–123.
- Воронов А. Я., Кашпарова В. С., Синицын В. Ю. Тест NEO PI-R как инструмент исследования психологического портрета студента // Материалы XVIII международной конференции «Применение новых технологий в образовании» («ИТО-Троицк-2007») 27–28 июня 2007 г. — Троицк, 2007. — С. 314–316.
- Жуков М. Л. Разработка искусственных нейронных сетей для прогнозирования психологических характеристик личности на основе опросника NEO PI-R: выпускная квалификационная работа. — М.: РГГУ, 2017.
- Кабаков Р. R в действии. Анализ и визуализация данных в программе R / пер. с англ. Полины А. Волковой. — М.: ДМК Пресс, 2014. — 588 с.
- Кашпарова В. С., Синицын В. Ю. О построении новых психометрических шкал на основе многошкального личностного опросника NEO PI-R // Наука и современность. — 2013. — № 26–1. — С. 180–183.
- Кашпарова В. С., Синицын В. Ю. Оценивание показателей надёжности психометрических шкал теста NEO PI-R при помощи численного ресамплинга // Достижения вузовской науки. — 2014. — № 13. — С. 73–77.
- Кондрашова О. В. Построение и использование нейронных сетей для статистического анализа данных анкетирования по тесту NEO PI-R: Дипл. раб. — М.: РГГУ, 2004.
- Синицын В. Ю., Кашпарова В. С. Психометрические свойства теста NEO PI-R и его применение для исследования психологического портрета студента // Психолого-педагогические исследования в системе образования: Материалы II Всероссийской научно-практической конференции: в 5 ч. Ч. 4 / Акад. повышен. квалиф. и перепод. раб. обр.; Южно-Уральск. гос. ун-т; Челяб. гос. пед. ун-т; Челяб. ин-т доп. проф.-пед. образ. — М., Челябинск, 2004. — C. 31–34.
- Шитиков В. К., Розенберг Г. С. Рандомизация и бутстреп: статистический анализ в биологии и экологии с использованием R. — Тольятти: Кассандра, 2013. — 314 c.
- Шитиков В. К., Мастицкий С. Э. (2017) Классификация, регрессия и другие алгоритмы Data Mining с использованием R. 351 с. − Электронная книга, адрес доступа: https://github.com/ranalytics/data-mining
- Эфрон Б. Нетрадиционные методы многомерного статистического анализа: Сб. статей: Пер. с англ./Предисловие Ю. П. Адлера, Ю. А. Кошевника. — М.: Финансы и статистика, 1988. — 263 с.

