{{{Исследование определения теплового состояния паропроводов при пуске Т-110/120-130 на базе обратной задачи теплопроводности
Семенов Алексей Олегович, аспирант;
Мустафина Эльвина Рафаиловна, студент
Уфимский государственный авиационный технический университет}}}
Для паротурбинных установок (ПТУ), обеспечивающих выработку электрической и тепловой энергии, характерно очень большое количество возможных режимов работы, связанных с постоянно меняющимися электрическими и тепловыми нагрузками.
Существуют стационарные режимы, при которых параметры пара и тепловое состояние элементов конструкции турбоагрегата не меняются с течением времени, и нестационарные (переходные) режимы эксплуатации, связанные с изменением теплового состояния турбины при переходе из одного состояния в другое при изменении электрической или тепловой нагрузки, а также пуски и остановы. Отличительной особенностью переходных режимов является возможность возникновения опасных температурных напряжений, которые могут привести к разрушению оборудования.
Пуск ПТУ является нестационарным режимом, при котором тепловое состояние энергетической установки и её отдельных элементов претерпевает наибольшее изменение. При неправильно выбранной скорости прогрева появляется риск возникновения температурных напряжений, превосходящих допустимые. Ситуация осложняется также свойствами отдельных элементов установки и условиями нагрева, что приводит к тому, что одни элементы конструкции прогреваются быстрее (медленнее) других. Например, при пуске ротор турбины прогревается намного быстрее цилиндра и его фланцевых соединений. В инструкциях по эксплуатации турбоагрегата приводятся критерии безопасного состояния и их величины, которые позволяют лишь поверхностно судить о теплонапряженном состоянии элементов оборудования при пусках.
Разработка технологий для получения информации о теплонапряженном состоянии позволит повысить надежность эксплуатации энергетического оборудования, снизить пусковые напряжения и продлить срок службы ПТУ.
В данной работе проводится определение теплового состояния паропровода паровой турбины на основе решения ОЗТ (обратной задачи теплопроводности). В работе показана правомерность использования аналитического решения ОЗТ для идентификации параметров граничных условий. Исходной информацией для решения являлись экспериментальные данные пусковых операций турбоагрегата Т-110/120–130, предоставленные Уфимской ТЭЦ-2.
На рисунке 1 представлен чертеж паропровода турбины Т-110/120–130. [2]
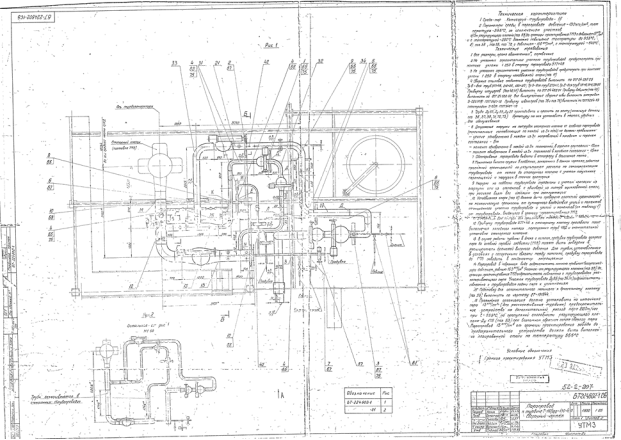
Рис. 1. Паропровод к турбине Т-110/120–130
Исследуемый паропровод имеет следующие измерения: наружный диаметр 273 мм, толщина паропровода (отношение наружного к внутреннему диаметру) 36 мм.
Были получены экспериментальные данные на Уфимской ТЭЦ-2 в ходе пуска турбины из горячего состояния. (см. Табл. 1) Начало прогрева: 01.10.2016 в 22:00.
Таблица 1
Экспериментальные данные
|
01.10.2016 22:00:00 |
24.93 |
|
01.10.2016 22:01:00 |
24.94 |
|
01.10.2016 22:02:00 |
24.94 |
|
01.10.2016 22:03:00 |
24.96 |
|
01.10.2016 22:04:00 |
24.96 |
|
01.10.2016 22:05:00 |
24.99 |
|
01.10.2016 22:06:00 |
25.38 |
|
01.10.2016 22:07:00 |
27.77 |
|
01.10.2016 22:08:00 |
36.22 |
|
01.10.2016 22:09:00 |
47.48 |
|
01.10.2016 22:10:00 |
57.53 |
|
01.10.2016 22:11:00 |
66.04 |
|
01.10.2016 22:12:00 |
73.27 |
|
01.10.2016 22:13:00 |
79.4 |
|
01.10.2016 22:14:00 |
84.6 |
|
01.10.2016 22:16:00 |
92.77 |
|
01.10.2016 22:17:00 |
96.03 |
|
01.10.2016 22:18:00 |
98.88 |
|
01.10.2016 22:19:00 |
101.44 |
|
01.10.2016 22:20:00 |
103.76 |
|
01.10.2016 22:21:00 |
105.9 |
|
01.10.2016 22:22:00 |
107.88 |
|
01.10.2016 22:23:00 |
109.77 |
|
01.10.2016 22:24:00 |
111.55 |
|
01.10.2016 22:25:00 |
113.29 |
|
01.10.2016 22:26:00 |
114.97 |
|
01.10.2016 22:27:00 |
116.6 |
|
01.10.2016 22:28:00 |
118.2 |
|
01.10.2016 22:29:00 |
119.77 |
|
01.10.2016 22:30:00 |
121.34 |
|
01.10.2016 22:31:00 |
122.89 |
|
01.10.2016 22:32:00 |
124.44 |
|
01.10.2016 22:33:00 |
125.94 |
|
01.10.2016 22:34:00 |
127.4 |
|
01.10.2016 22:35:00 |
128.85 |
|
01.10.2016 22:36:00 |
130.29 |
|
01.10.2016 22:37:00 |
131.67 |
|
01.10.2016 22:38:00 |
132.99 |
|
01.10.2016 22:39:00 |
134.25 |
|
01.10.2016 22:40:00 |
135.46 |
|
01.10.2016 22:41:00 |
136.61 |
|
01.10.2016 22:42:00 |
137.68 |
|
01.10.2016 22:43:00 |
138.69 |
|
01.10.2016 22:44:00 |
139.67 |
|
01.10.2016 22:45:00 |
140.56 |
|
01.10.2016 22:46:00 |
141.43 |
|
01.10.2016 22:47:00 |
142.25 |
|
01.10.2016 22:48:00 |
143.04 |
|
01.10.2016 22:49:00 |
143.75 |
|
01.10.2016 22:50:00 |
144.46 |
|
01.10.2016 22:51:00 |
145.09 |
|
01.10.2016 22:52:00 |
145.72 |
|
01.10.2016 22:53:00 |
146.3 |
|
01.10.2016 22:54:00 |
146.88 |
|
01.10.2016 22:55:00 |
147.43 |
|
01.10.2016 22:56:00 |
147.92 |
|
01.10.2016 22:57:00 |
148.41 |
|
01.10.2016 22:58:00 |
148.86 |
|
01.10.2016 22:59:00 |
149.29 |
|
01.10.2016 23:00:00 |
149.68 |
|
01.10.2016 23:01:00 |
150.04 |
|
01.10.2016 23:03:00 |
150.71 |
|
01.10.2016 23:04:00 |
150.99 |
|
01.10.2016 23:05:00 |
151.26 |
|
01.10.2016 23:06:00 |
151.47 |
|
01.10.2016 23:07:00 |
151.65 |
|
01.10.2016 23:08:00 |
151.74 |
|
01.10.2016 23:09:00 |
151.81 |
|
01.10.2016 23:10:00 |
151.84 |
|
01.10.2016 23:11:00 |
151.8 |
|
01.10.2016 23:12:00 |
151.73 |
|
01.10.2016 23:13:00 |
151.64 |
|
01.10.2016 23:14:00 |
151.6 |
|
01.10.2016 23:15:00 |
151.57 |
|
01.10.2016 23:16:00 |
151.55 |
|
01.10.2016 23:17:00 |
151.53 |
|
01.10.2016 23:18:00 |
151.51 |
|
01.10.2016 23:19:00 |
151.48 |
|
01.10.2016 23:20:00 |
151.49 |
|
01.10.2016 23:21:00 |
152.51 |
|
01.10.2016 23:22:00 |
155.58 |
|
01.10.2016 23:23:00 |
159.84 |
|
01.10.2016 23:24:00 |
164.78 |
|
01.10.2016 23:25:00 |
168.43 |
|
01.10.2016 23:26:00 |
166.18 |
|
01.10.2016 23:27:00 |
165.91 |
|
01.10.2016 23:28:00 |
167.4 |
|
01.10.2016 23:29:00 |
169.65 |
|
01.10.2016 23:30:00 |
172.46 |
|
01.10.2016 23:31:00 |
175.35 |
|
01.10.2016 23:32:00 |
178.02 |
|
01.10.2016 23:33:00 |
180.45 |
|
01.10.2016 23:34:00 |
182.57 |
|
01.10.2016 23:35:00 |
184.37 |
|
01.10.2016 23:36:00 |
185.98 |
|
01.10.2016 23:37:00 |
187.41 |
|
01.10.2016 23:38:00 |
188.69 |
|
01.10.2016 23:39:00 |
189.81 |
|
01.10.2016 23:40:00 |
190.73 |
|
01.10.2016 23:41:00 |
191.54 |
|
01.10.2016 23:42:00 |
192.27 |
|
01.10.2016 23:43:00 |
192.96 |
|
01.10.2016 23:44:00 |
193.62 |
|
01.10.2016 23:45:00 |
194.23 |
|
01.10.2016 23:46:00 |
194.81 |
|
01.10.2016 23:47:00 |
195.4 |
|
01.10.2016 23:48:00 |
195.96 |
|
01.10.2016 23:50:00 |
197.07 |
|
01.10.2016 23:51:00 |
197.64 |
|
01.10.2016 23:52:00 |
198.23 |
|
01.10.2016 23:53:00 |
198.82 |
|
01.10.2016 23:54:00 |
199.42 |
|
01.10.2016 23:55:00 |
200.03 |
|
01.10.2016 23:56:00 |
200.64 |
|
01.10.2016 23:57:00 |
201.25 |
|
01.10.2016 23:58:00 |
201.87 |
|
01.10.2016 23:59:00 |
202.51 |
|
02.10.2016 00:00:00 |
203.15 |
Экспериментальные значения температур внутри паропровода необходимы для решения данной обратной задачи нестационарной теплопроводности (ОЗТ), в то время как для решения прямой задачи теплопроводности (ПЗТ) в объем предварительных сведений включаются теплофизические свойства материала тела (коэффициент теплопроводности, удельная теплоемкость и плотность), начальное распределение температуры и параметры граничных условий (температура или плотность теплового потока на ограничивающих поверхностях тела, коэффициент теплоотдачи и температура омывающей тело жидкости или газа).
При решении ОЗТ не нужно знать начального распределения температуры в теле, что является несомненным достоинством метода ОЗТ. Т. к. мы имеем паропровод, то рассматривать граничную ОЗТ будем для неограниченной пластины с идеальной тепловой изоляцией.
|
Обозначения |
|
|
x–координата; τ–время; T(x,τ)–температура; a–коэффициент температуропроводности материала; λ–теплопроводность материала; с–теплоемкость; ρ–плотность; |
Bi–критерий Био; Fo–критерий Фурье; α–коэффициент теплоотдачи; l0–полутолщина пластины; Tf,0–температура омывающей среды; T0–начальная температура. |
Аналитическое решение линейной одномерной обратной задачи теплопроводности на основе преобразования Лапласа
Следуя работе [1, с. 230], рассмотрена граничная обратная задача в постановке Коши для неограниченной пластины, которая содержит уравнение процесса нестационарной теплопроводности.
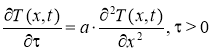 (1)
(1)
и установленные на одной из плоскостей (в точке х=0) зависимости от времени температуры
![]() (2)
(2)
и ее градиента
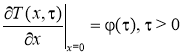 . (3)
. (3)
На рисунке 2 в качестве примера показаны распределения экспериментально установленных функций f(τ) и φ(τ).
Применяя к задаче (1)–(3) интегральное преобразование Лапласа по аргументу x
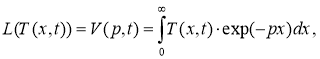 (4)
(4)
при аппроксимации зависимостей f(t) и φ(t) полиномами
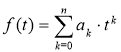 ,
, 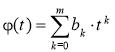 (5)
(5)
решение в оригиналах задачи (1)–(3) дает зависимость для искомого распределения температуры
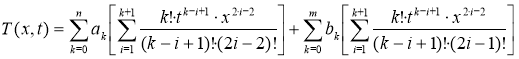
и модуля её градиента:
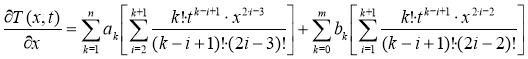 (6)
(6)
(здесь под t понимается величина, равная aτ).
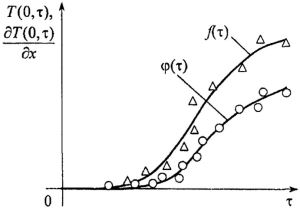
Рис. 2. Пример распределения температуры и ее градиента в пластине
Реализация расчётов
Аналитическое решение ПЗТ
Для решения ПЗТ был написан алгоритм расчета в среде Mathcad 15.0 по формулам, представленным в работе [3, с. 50]. Исходные данные для расчета представлены в таблице 2, а его результаты на рисунке 3.
Таблица 2
Исходные данные для расчета
|
Материал |
Сталь марки 15Х1М1Ф |
|
Толщина стенки, мм |
36 |
|
Коэффициент теплоотдачи, Вт/(м2К) |
55 |
|
Температура пара, 0С |
555 |
|
Начальная температура, 0С |
25 |
|
Коэффициент теплопроводности, Вт/(мК) |
33,44 |
|
Удельная теплоемкость, кДж/(кгК) |
0,58 |
|
Плотность, кг/м3 |
7800 |
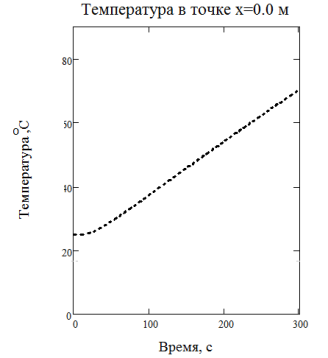
Рис. 3. Результат расчета ПЗТ для точки x=0 м
Использование аналитического решения ОЗТ
Исходными данными для расчета ОЗТ являлись приведенные на рисунке 2 результаты расчета ПЗТ. Аппроксимация решения ПЗТ производилась с помощью кубического сплайна [4], начиная с 13–ой секунды от начала нагревания пластины. Сравнение результатов решения ПЗТ и ОЗТ для точки х=0,018 м (в плоскости симметрии пластины) показало их практическое совпадение.
Затем при проведении расчетов ОЗТ на аналитическое решение ПЗТ для точки x=0 наносились помехи с использованием функции Гаусса, после чего была проведена полиномиальная аппроксимация исходной информации для получения решения ОЗТ с учётом возможных ошибок измерения входящих в неё параметров. На рисунке 4 и 5 представлена реализация наложения помех и результат сравнения ОЗТ до и после наложения помехи в точке x=0,018 м соответственно.
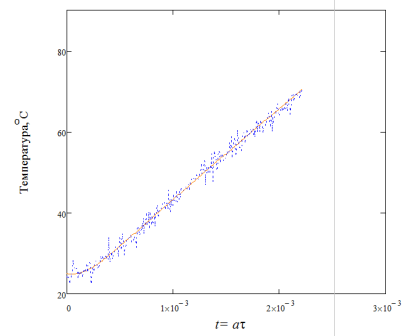
Рис. 4. Реализация наложения помехи
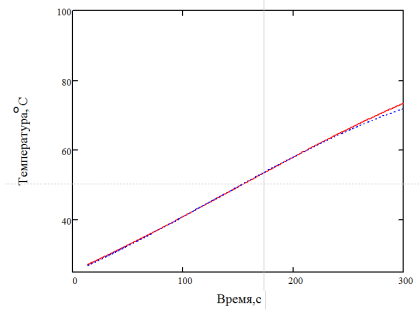
Рис. 5. Сравнение решений ОЗТ до и после наложения помех для точки х=0,018 м
Заключение
Показана правомерность использования аналитического решения ОЗТ для идентификации параметров граничных условий при отсутствии и наличии ошибок измерений параметров входной информации.
Литература:
- Цирельман Н. М. «Конвективный тепломассоперенос: моделирование, идентификация, интенсификация: монография; УГАТУ — Уфа, 2015. — 471 с.
- Инструкция по эксплуатации турбины Т-110/120–130–12,8 ст. № 6; Архив Уфимской ТЭЦ-2
- Цирельман Н. М. Теория и прикладные задачи тепломассопереноса/ Н. М. Цирельман. — М.: Машиностроение, 2011. — 503 с.
- Методы сплайн–функций. Завьялов Ю. С., Квасов Б. И., Мирошниченко В. Л. — М.: Наука, 1980. — 500 с.







