Рассмотрены вопросы теоретического обоснования оптимизации состава дизельного топлива, полученного из нефти Талаканского месторождения (Якутия) с депрессорной присадкой Difron 315. Показана математическая модель состава топлива. Определены коэффициенты регрессии на основе метода наименьших квадратов. Кривые, полученные в результате оптимизации концентрации присадки Difron 315 и представлена в виде полиномы 2-го рода.

Ключевые слова: депрессорная присадка, метод наименьших квадратов, коэффициенты регрессии, химмотологический процесс, температура застывания, предельная температура фильтруемости, параметры оптимизации

Математические модели химмотологических процессов в общем случае представляют собой нелинейные дифференциальные или интегрально-дифференциальные уравнения с переменными коэффициентами, которые в настоящее время в явном виде получены и решены, не могут [1]. Поэтому строят статистические модели на основе эмпирического подхода, что приводит к представлению математических моделей химмотологических процессов в виде алгебраических полиномов, связывающих целевые показатели с факторами условий протекания процесса или составом топлива.

Для определения оптимальной концентрации присадки в дизельном топливе были составлены математические модели процесса в виде полинома второго порядка и определены его коэффициенты (,, ).

В качестве целевой функции Ү была выбрана температура застывания дизельного топлива в зависимости от концентрации присадки (). Записывалась она следующим уравнением [2]:

Оптимальную концентрацию присадки определяли по методу наименьших квадратов (МНК), применяемому для решения различных задач и основанному на минимизации суммы квадратов отклонений некоторых функций от искомых переменных [3]. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функцией [4]. Метод наименьших квадратов является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным [5].

Температуру застывания возле минимума достаточно описать близлежащими точками, так как она описывается квадратным уравнением ряда Фурье:

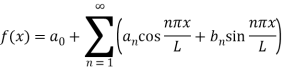
В табл. 1 показаны точки застывания возле минимума.

Таблица 1

Концентрации присадки Difron 315 итемпературы застывания

Рис. 1. Полиномиальная кривая зависимости температуры застывания от концентрации присадки

Из данных рис. 1 следует, что целевая функция

.

Следовательно, коэффициенты регрессии будут равны:

= 102,44,

= 572,06,

= 528,77,

Возле минимума функцию температуры можно аппроксимировать квадратичной функцией, как видно из графика, коэффициент . В зависимости от концентрации присадки температура застывания сначала будет понижаться, а потом увеличиваться. Параметры оптимизации приведены в табл. 2, а полиномиальные кривые показаны на рис. 2.

Таблица 2

Экспериментальная ирасчетная концентрации присадки Difron 315

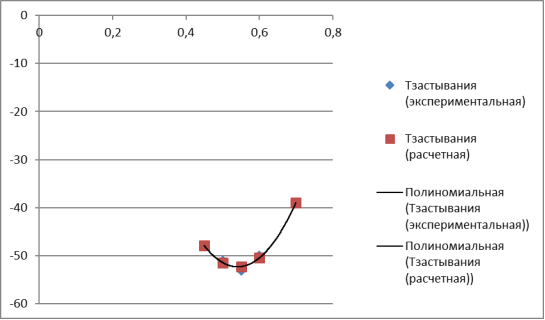
Рис. 2. Полиномиальные кривые зависимости температуры застывания от концентрации присадки (экспериментальная и расчетная)

Заключение

Математическая модель присадки Difron 315 представляет собой полиномиальные кривые в виде параболы. Теоретически обосновано экспериментальная работа, в ходе чего выявлено оптимальные концентрации депрессорных присадок в составе топлива, выделенного из нефти Талаканского месторождения (Якутия).

Литература:

1. Гуреев А. А., Азев B. C., Камфер Г. М. Топлива для дизелей. Свойства и применение. М., Химия, 1993. 330 с.
2. Справочник по математике для инженеров и учащихся втузов. Бронштейн И. Н., Семендяев К. А. М.: Наука, 1981. 720с., ил.
3. Линник Ю. В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений. 2-е изд. М., 1962.
4. Айвазян С. А. Прикладная статистика. Основы эконометрики. Том 2. М.: Юнити-Дана, 2001. 432 с. ISBN 5–238–00305–6.
5. Александрова Н. В. История математических терминов, понятий, обозначений: словарь-справочник. 3-е изд. Шаблон: Указание места в библио ссылке: ЛКИ, 2008. 248 с. ISBN 978–5-382–00839–4.