Математизация смешанного тестирования на примере тестов расширения умений



Под дидактической единицей будем понимать наименьшее знание, которое может распадаться на такие составляющие, как знание, умение, навыки.

Данные дидактические единицы мы выбираем сами. В теории можно каждую дидактическую единицу знания, углубить до дидактической единицы умения. Таким образом, появляется управление дидактическими единицами, т. е. в зависимости от того, что нам необходимо получить для освоения компетенции, мы можем углублять дидактические единицы до необходимого уровня, и оценивать их освоение в соответствии с данным уровнем.

Определив дидактические единицы, которые будут являться дидактическими единицами, несущими в себе как знания, так и умения, выделим типы тестов, с помощью которых можно проверить уровень знание различных типов дидактических единиц. Вопрос типизирования тестов можно рассматривать с двух сторон. Содной тестирование проводится независимо по знаниям и умениям. Такой подход можно назвать обособленным. Сдругой стороны можно проводить смешанное тестирование, в котором будут вопросы, как на выявление знаний, так и на определение умений.

Обособленное тестирование рассматривалось в предыдущих работах [2], там дается более подробное описание различных вариаций тестов для обособленного тестирования, возможные пути оценивания данных тестов, а также преимущества и недостатки подобных тестов.

Для оценки дидактических единиц, можно также использовать смешанное тестирование. В подобном тестировании происходит проверка нескольких типов дидактических единиц. Важной задачей в составлении подобных тесов, это правильно оценить его их результаты. К смешанному тестированию можно также отнести тесты, которые проверяют несколько подуровней знаний. Например, тестирование дидактических единиц как знаний с одним вариантом ответа, так и знаний, которые предполагают несколько вариантов ответов. Такая же ситуация обстоит и с дидактическими единицами, которые несут в себе умения

Первый тип тестирования, который можно выделить в данном контексте, это тестирование расширения умений. Данный тип может относиться, как к смешанному тестированию, так и к обособленному. В таком случае, если проверка заключается в тестировании исходных умений, на основе которых строятся остальные умения, то данный тип тестирования можно отнести к обособленному тестированию. Тогда данный тип тестирования можно проводить в игровой форме. Под игровой формой подразумевается создание программы, или компьютерной игры, в которых будет представлена задача, требующая умения принимать правильное направление в расширении текущих умений и знаний. В таком тестировании оценка будет смещаться с правильного ответа на ход мысли человека, т. е. человек изначально попадает в ситуацию, в которой он, скорее всего, не знает ответ на 100 %, поэтому ему необходимо с помощью уже имеющихся умений найти примерный вектор решения задачи. Оценка зависит от того, насколько близко совпал вектор мысли с правильным ответом. Такой тип тестирования умений можно обозначить как тесты расширения умений.

Схема тестирования расширения умений, будет представляться следующим образом:

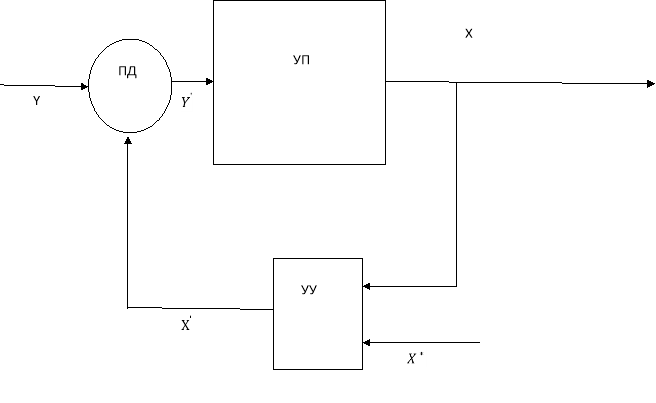
Рис. 1. Схема тестирования с тестами расширения умений, где:

‒ УП — блок тестов для тестирования умений;

‒ УУ — управляющее устройство, которое сравнивает полученные результаты теста с идеалом, и производит корректировку или воздействие, и подает данные воздействия на блок УП;

‒ преобразованные ДЕ умения;

‒ управляющее воздействие на основные умения;

‒ текущий результат тестирования;

‒ желаемый результат тестирования.

В данном тестировании, желаемый результат находится в некотором диапазоне:

Equation Section (Next)(1)

Данный диапазон предполагает, что студент должен ответить приблизительно, и оценка его ответа, должна попадать в желаемый диапазон.

В случае, если оценка ответа студента не попадает в желаемы интервал, тогда необходимо провести исследование проблематики тестирования, или знаний студента, и на основе выявленных данных предоставить само управляющее воздействие.

С математической точки зрения, управляющее воздействие, будет представлено как некоторой формулой:

Equation Section (Next)(2)

Полученное управляющее воздействие необходимо применить к имеющемуся уровню умений студента, что приводит к преобразованию ДЕ умения. С математической точки зрения, данную операцию можно выразить как

Equation Section (Next)(3)

После преобразования умений, происходит проверка успешности их преобразования, и соответственно успешность управляющего воздействия, т. е. происходит повторное тестирование, до тех пор, пока конечный результат не будет удовлетворять желаемому. Таким образом, можно представить конечный результат в виде некоторой формулы:

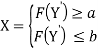Equation Section (Next)(4)

где:

‒ верхняя граница вектора;

‒ нижняя граница вектора.

По-другому обстоит дело с тестами расширения умения в случае если тестируемые умения, основываются на предыдущих умениях. Такие умения можно определить как: косвенные умения. Под косвенными умениями можно понимать умения, которые были получены студентом от других дисциплин, материалов, предыдущих тем лекций, предметов, бытовых взаимодействий с приборами, людьми, умения жизненного опыта. Например, тестирование студента по векторной алгебре, не может быть проведено без знания студента, что такое вектор, что такое алгебра, умения писать, читать, держать ручку и. д. В таком контексте рассмотрения тестирования, можно всегда рассматривать студента как некоторый черный ящик, который постоянно подвергается проверке на функционирование, и в случае не прохождения данной проверки, этот черный ящик должен подвергаться сопутствующим проверкам.

Косвенное тестирование умений, в тестах на расширения умений, как раз и относится к одним из таких сопутствующих проверок. Имеется два варианта проведения таких проверок. В первом случае, если студент не прошел основной тест на расширение умений, тогда он подвергается проверке на состояние его косвенных умений. Чтобы не проводить тестирование всех подряд умений студента, необходимо определить круг тестируемых умений, внешнюю среду для основных умений.

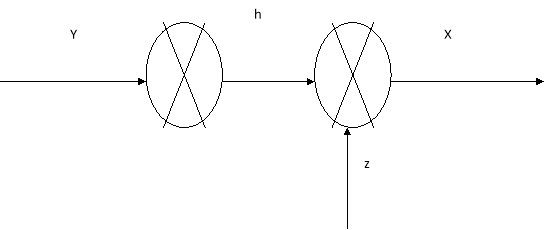
Рис. 2. Схема тестирования умений, косвенный тип тестирования, где:

‒ — — тестирование;

‒ Y — косвенные умения;

‒ h — влияние косвенных умений;

‒ Z — умения по тестируемому разделу изучаемой дисциплины, или основные умения;

‒ X — результат по тестированию основных умений.

Данный график можно представить в виде некоторой функции, которая будет характеризовать результат тестирования основных умений:

Equation Section (Next)(5)

После того как была определена внешняя среда, для тестирования косвенных умений, имеется два варианта, проведения процесса тестирования умений. При первом варианте, сначала происходит тестирование внешней среды, на ее соответствие к желаемым результатам. Тогда схема тестирования повторяет схему на Рис. 1, но только применяется данная схема для тестирования именно косвенных умений. Все формулы также подойдут и для косвенных умений. После того как косвенные умения будут соответствовать желаемому результату, происходит переход к тестированию основных умений.

При втором случае, проведения тестирования расширения умений, предполагается одновременная проверка, как косвенных умений, так и основных умений. При этом появляется два блока принятия решений, один предназначен для косвенных умений, другой для основных умений. Также появляется два управленческих решения.

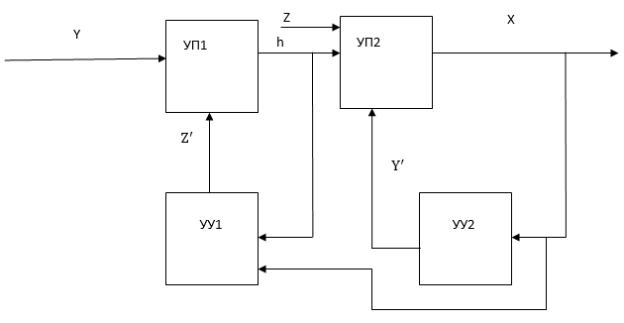
Рис. 3. Схема тестировании расширения умений с учетом косвенных умений, где:

‒ УП1 блок тестов для тестирования косвенных (внешних) умений;

‒ УП2 — блок тестов для тестирования основных умений;

‒ УУ — управляющее устройство, которое сравнивает полученные результаты теста с идеалом, и производит корректировку или воздействие, и подает данные воздействия на блок УП;

‒ управляющее воздействие на косвенные основные умения;

‒ управляющее воздействие на основные умения;

‒ управляющее воздействие на косвенные умения.

Тестирование расширения умений теперь учитывает косвенные умения. Итоговый результат также находится в некотором интервалом, но только теперь этот интервал состоит из большего числа переменных, что можно представить следующей формулой:

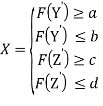Equation Section (Next)(6)

где:

‒ верхняя граница вектора для косвенных умений;

‒ нижняя граница вектора для косвенных умений.

А управляющее воздействие Z представляется в виде похожей формулы, как и для управляющего воздействия для основных умений:

Equation Section (Next)(7)

Данный подход можно применить и к остальным смешанным типам тестов, отличие будет заключаться в количестве тестируемых типов дидактических единиц, что приводит к увеличению входных данных для функций поиска управляющих воздействий.

Литература:

1. В. Е. Пешкова. Педагогика Часть 4. Теория обучения (дидактика) учеб. пособие для студ. вузов. — 2010: Майкоп, 2010. — 149 с.;
2. Бронов С. А., Мартынов А. В., Тесленко Д. С. Взаимосвязь дидактических единиц с тестами в контексте знаний, умений, навыков // Молодой ученый. — 2017. — № 20. — С. 433–436.
3. В. В. Конев Векторная. Алгебра: учеб. пособие для студ. вузов. — 2008г: Томский политехнический университет, 2008г. — 34 с.;
4. В. Е. Пешкова. Педагогика Часть 6. Педагогическая информатика (дидактика) учеб. пособие для студ. вузов. — 2010: Майкоп, 2010. — 151 с.;
5. Голованова Ю. В. Модульность в образовании: методики, сущность, технологии // Молодой ученый. — 2013. — № 12. — С. 422–437;