В статье рассматривается задача механики разрушения о взаимодействии ортотропных упругих включений, поверхность которых равномерно покрыта однородной пленкой, и прямолинейных зон предразрушения со связями между берегами коллинеарных осям абсцисс и ординат в изотропной плоскости. Предложена модель зарождения трещин в композитах с двоякопериодической структурой, основанная на рассмотрении зоны трещинообразования. Принято, что зона трещинообразования представляет собой слой конечной длины, содержащей материал с частично нарушенными связями между отдельными структурными элементами.
Строятся общие представления решений, описывающие класс задач с двоякопериодическим распределением напряжений вне круговых отверстий и прямолинейных трещин. Удовлетворяя граничным условиям на контурах круговых отверстий и берегах трещин, получена бесконечная алгебраическая система и явно сингулярное интегральное уравнение. Затем используя прямые методы, решение интегрального уравнения сведено к конечной алгебраической системе. Численная реализация изложенного способа приведена на IBM. Вычислены коэффициенты интенсивности напряжений в зависимости от геометрических параметров рассматриваемой среды.
Ключевые слова: двоякопериодическая решетка, средние напряжения, граничные условия, продольный сдвиг, линейные алгебраические уравнения, сингулярные уравнения, ортотропные упругие включения, зона предразрушения
Введение. В технике широкое распространение получили волокнистые композиционные материалы, армированные высокопрочными и высокомодульными непрерывными волокнами, в которых армирующие элементы несут основную нагрузку, тогда как матрица передаёт напряжения волокнам. Волокнистые композиционные материалы, как правило, анизотропны. Механические свойства композиционных материалов определяются не только свойствами самих волокон, но и их ориентацией, объёмным содержанием, способностью матрицы передавать волокнам приложенную нагрузку и др.
Интерес к исследованию трещинообразования в композитах напрямую связан с проектированием новых высокопрочных материалов. В связи с этим разработка математических моделей трещин в композитах весьма актуальна. Актуальность таких исследований вызвана широким использованием в технике конструкций и изделий из композиционных материалов. Исследования по разработке математических моделей теоретически описываемого напряженно–деформируемого состояния армированного композита вблизи включения при сдвиге и трещин практически отсутствуют.
Цель работы состоит в разработке новой математической модели трещин сдвига в композите.
Постановка задачи. Пусть двоякопериодическая решетка с круговыми отверстиями, имеет радиус ![]() и центры в точках:
и центры в точках:
![]()
![]()
Круговые отверстия плоскости (связующего) заполнены волокнами (шайбами) из другого ортотропного упругого материала, поверхность которых равномерна покрыта однородной цилиндрической пленкой. Плоскость ослаблена двумя периодическими системами прямолинейных трещин (рис. 1). Плоскость подвергнута сдвигу усилиями (сдвиг на бесконечности). Берега трещин свободны от внешних нагрузок, а на композит действуют напряжения ![]() ,
, ![]() (продольный сдвиг на бесконечности).
(продольный сдвиг на бесконечности).
По мере возрастания внешней нагрузки
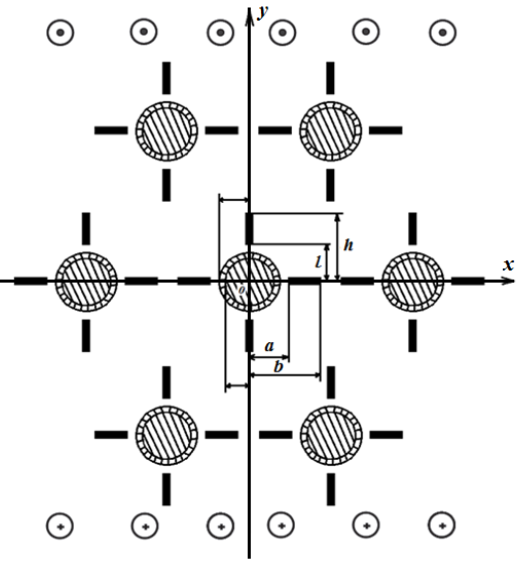
Рис. 1. Расчетная схема задачи механики разрушения о трещины в композите, армированном однонаправленными ортотропными волокнами
При деформации кусочно-однородного составного тела в случае идеального контакта смежные точки контуров на границе «включение — покрытие», а также «покрытие — плоскость» будут иметь одинаковые перемещения и напряжения.
Напряжения и смещение можно выразить через аналитическую функцию [16]
![]()
![]()
![]()
![]()
где ![]() постоянная материала среды;
постоянная материала среды; ![]()
Краевые условия поставленной задачи запишем в виде
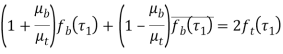 (1)
(1)
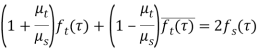 (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
где ![]()
![]() полярный угол,
полярный угол, ![]() толщина покрытия,
толщина покрытия, ![]() и
и ![]() –аффикс точек берегов трещин, направленных по осям абсцисс и ординат, соответственно.
–аффикс точек берегов трещин, направленных по осям абсцисс и ординат, соответственно.
Величины, относящиеся к покрытию, волокну и связующему, в дальнейшем отмечаются соответственно индексами ![]() и
и ![]() .
.
![]() на берегах зон предразрушения коллинеарных оси абсцисс;
на берегах зон предразрушения коллинеарных оси абсцисс; ![]() на берегах зон предразрушения коллинеарных оси ординат.
на берегах зон предразрушения коллинеарных оси ординат.
Рассматриваемая задача дополняется соотношениями, связывающими сдвиг берегов зон предразрушения и усилия в связях. Без потери общности эти соотношения представим в виде
![]() (5)
(5)
![]() (6)
(6)
где функции
Решение краевой задачи пишем в виде [16, 17]
![]() (7)
(7)
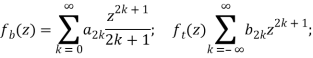 (8)
(8)
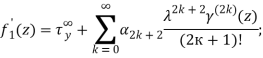
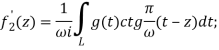 (9)
(9)
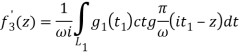
где интегралы в (9) берутся по линии ![]() и
и ![]() — функции Вейерштрасса [2],
— функции Вейерштрасса [2], ![]() искомые функции, характеризующие сдвиг берегов зон предразрушения:
искомые функции, характеризующие сдвиг берегов зон предразрушения:
![]() на
на ![]()
![]() на
на ![]()
К основным представлениям (7)–(9) добавляются дополнительные условия, вытекающие из физического смысла задачи
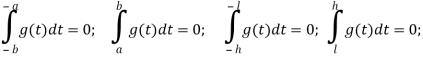 (10)
(10)
Напомним обшей сведения [2] из теории упругости анизотропных тел. Введем обозначения
![]() и
и ![]() ,
, ![]() –комплексный параметр.
–комплексный параметр.
Задача об антиплоской деформации (сложный сдвиг) анизотропного тела сводится [18] к такой же задаче для изотропного тела, у которого поперечное сечение определяется путем аффинного преобразования
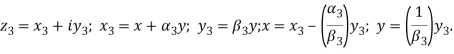
Остановимся кратко на случае ортотропного стержня. Направляя оси ![]() и
и ![]() нормально к плоскостям упругой симметрии, запишем уравнения обобщенного закона Гука так:
нормально к плоскостям упругой симметрии, запишем уравнения обобщенного закона Гука так:
![]()
![]() – модуль сдвига для плоскостей
– модуль сдвига для плоскостей ![]() и
и ![]() .
.
Задача о продольном сдвиге ортотропного тела легко свести к задаче для изотропного тела несколькими способами, вводя в замену переменных. Одна из замен такова:
![]()
Решение краевой задачи. Неизвестная функция ![]() и постоянные
и постоянные ![]() должны быть определены из краевых условий (1)–(4). Для составления уравнений относительно неизвестных коэффициентов
должны быть определены из краевых условий (1)–(4). Для составления уравнений относительно неизвестных коэффициентов ![]() в функцию
в функцию ![]() представим граничное условие (1) в виде
представим граничное условие (1) в виде
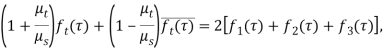 (11)
(11)
Относительно функций ![]() и
и ![]() будем считать, что они разлагаются на контуре
будем считать, что они разлагаются на контуре ![]() в ряды Фурье.
в ряды Фурье.
Для вывода разрешающих уравнений подставим в граничные условия (1)–(2) вместо функций ![]() их разложения в ряды Лорана в окрестности нулевой точки, а вместо
их разложения в ряды Лорана в окрестности нулевой точки, а вместо ![]() и
и ![]() ряды Фурье на контуре
ряды Фурье на контуре ![]() и приравнивая коэффициенты при одинаковых степенях
и приравнивая коэффициенты при одинаковых степенях ![]() в обеих частях краевых условий, получим после некоторые преобразований совокупность бесконечных систем линейных алгебраических уравнений:
в обеих частях краевых условий, получим после некоторые преобразований совокупность бесконечных систем линейных алгебраических уравнений:
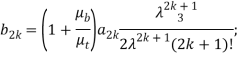
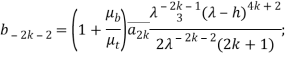
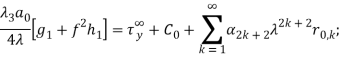
(12)
![]()
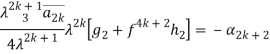
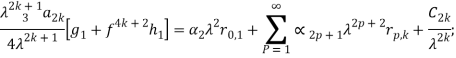
Здесь
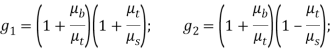
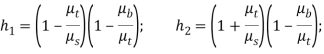
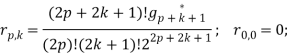
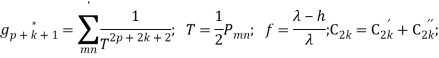
![]()
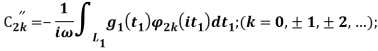
![]()
![]()
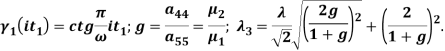
Требуя теперь, чтобы функции (7)–(9) удовлетворяли граничному условию на берегах зон предразрушения, получим систему двух сингулярных интегральных уравнений относительно ![]() и
и ![]()
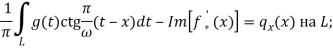
(13)
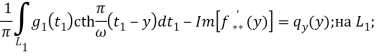
где ![]()
Алгебраическая система (12) совместно с сингулярными интегральными уравнениями (13) являются основными разрешающими уравнениями задачи, решение которых позволяет определить ![]() и коэффициенты
и коэффициенты ![]() Алгебраическая система (12) и интегральное уравнение (13) оказались связанными между собой и должны решаться совместно.
Алгебраическая система (12) и интегральное уравнение (13) оказались связанными между собой и должны решаться совместно.
Зная функции ![]() можно найти напряженно–деформированное состояние пластины.
можно найти напряженно–деформированное состояние пластины.
Величины, характеризующие длину зон предразрушения, входят разрешающие уравнения как неизвестные параметры, подлежащие определению. Так как в составном теле напряжения ограничены, то решение каждого сингулярного интегрального уравнения (13) следует искать в классе всюду ограниченных функций.
Воспользовавшись разложением функции ![]() в основной полосе периодов, а также учитывая,
в основной полосе периодов, а также учитывая, ![]() и
и ![]() применяя замену переменных, уравнение (13) проводится к стандартной форме.
применяя замену переменных, уравнение (13) проводится к стандартной форме.
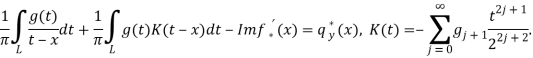 (14)
(14)
В дальнейшем преобразуем интегральное уравнение (14) к виду, удобному для нахождения его численного решения. Используя условие ![]() уравнение (14) примет вид:
уравнение (14) примет вид:
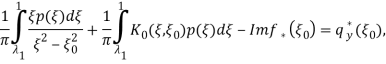
![]()
Чтобы перейти к стандартному отрезку интегрирования [1, 1] сделаем замену переменных
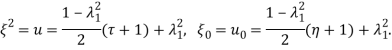 (15)
(15)
В результате преобразованное уравнение (14) принимает форму
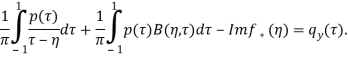 (16)
(16)
Здесь
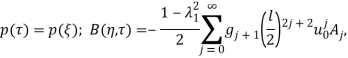
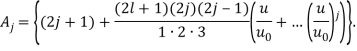
Решение интегрального уравнения (16) ищем в виде [16]:
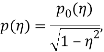 (17)
(17)
где ![]() непрерывна по Гельдеру на [1, 1], причем она аппроксимируется интерполяционным многочленом Лагранжа, построенным по чебышевским узлам.
непрерывна по Гельдеру на [1, 1], причем она аппроксимируется интерполяционным многочленом Лагранжа, построенным по чебышевским узлам.
Используя квадратурные формулы [10, 11]
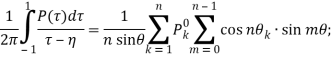
(18)
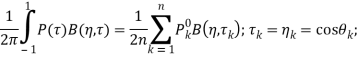
![]()
(19)
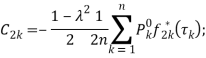
![]()
сведем основные разрешающие уравнения (12) и (14) к совокупности бесконечных систем линейных алгебраических уравнений и к двум конечным системам относительно приближенных значений ![]() и
и ![]() искомых функций в узловых точках.
искомых функций в узловых точках.
Конечные системы уравнений относительно неизвестных ![]() и
и ![]() имеют вид
имеют вид
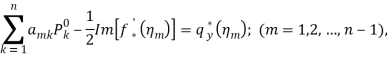
(20)
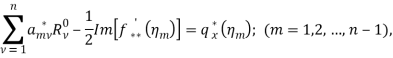
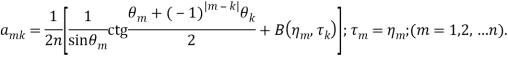
Так же определяются коэффициенты ![]()
К системе (20) необходимо добавить дополнительные условия (10), которые в дискретном виде имеют следующий вид:
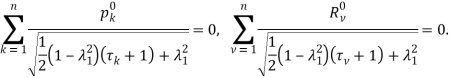 (21)
(21)
В правую часть полученных систем входят неизвестные значения напряжений ![]() и
и ![]() в узловых точках, принадлежащих концевым зонам
в узловых точках, принадлежащих концевым зонам ![]() и
и ![]() соответственно. Неизвестные напряжения в связях
соответственно. Неизвестные напряжения в связях ![]() и
и ![]() определяются из дополнительных условий (5), (6). Используя полученное решение, имеем
определяются из дополнительных условий (5), (6). Используя полученное решение, имеем
![]() (22)
(22)
![]() (23)
(23)
Полученная система уравнений (20)–(23) является связанной (замыкается) с бесконечными системами (12), в которых вместо ![]() подставлена формула (18). Система уравнений (12), (20) — (24) полностью определяет решение задачи.
подставлена формула (18). Система уравнений (12), (20) — (24) полностью определяет решение задачи.
После определения значений ![]() и
и ![]() коэффициенты интенсивности напряжений
коэффициенты интенсивности напряжений ![]() находятся на основании соотношений.
находятся на основании соотношений.
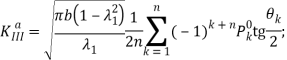
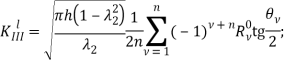
(24)
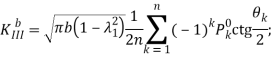
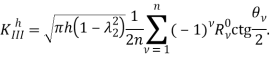
Меняя отношение жесткости волокна к жесткости связующего, можно получить все варианты, начиная со свободного от сил кругового отверстия и кончая абсолютно жестким включением.
Для анализа предельного равновесия трещин с концевыми зонами необходимы два условия (двухпараметрический критерий) разрушения. Первый критерий — это условие продвижения вершины трещины, а второй — это условие разрыва связей на краю концевой зоны. В качестве первого условия разрушения используем силовой критерий разрушения Ирвина. Состоянию предельного равновесия вершины трещины соответствует выполнение условия
![]() (25)
(25)
где ![]() постоянная материала, определяемая опытным путем.
постоянная материала, определяемая опытным путем.
В качестве второго условия разрушения используем критерий критического сдвига трещины и считаем, что предельный сдвиг связей на краю концевой зоны ![]() и
и ![]() или
или ![]() и
и ![]() происходит при выполнении условий
происходит при выполнении условий
![]()
(26)
![]()
где ![]() трещиностойкость материала связующего.
трещиностойкость материала связующего.
Решение системы полученных алгебраических уравнений позволяет (при заданной длине трещин и характеристик связей) найти критическую внешнюю нагрузку ![]() и предельный сдвиг берега концевой зоны в состоянии предельного равновесия трещин. Для заданных размеров трещин и концевых зон, используя предельные значения
и предельный сдвиг берега концевой зоны в состоянии предельного равновесия трещин. Для заданных размеров трещин и концевых зон, используя предельные значения ![]() и
и ![]() можно выделить режимы равновесия и роста трещин при монотонном нагруженный. Если выполняются условия
можно выделить режимы равновесия и роста трещин при монотонном нагруженный. Если выполняются условия ![]() то происходит продвижение вершины трещин с одновременным увеличением длины концевой зоны без разрыва связей. Этот этап развития трещин продольного сдвига можно рассматривать, как процесс приспособляемости к заданному уровню внешних нагрузок.
то происходит продвижение вершины трещин с одновременным увеличением длины концевой зоны без разрыва связей. Этот этап развития трещин продольного сдвига можно рассматривать, как процесс приспособляемости к заданному уровню внешних нагрузок.
Рост вершины трещины с одновременным разрушением связей на краю концевой зоны будет происходить при выполнении условий
![]()
Так, например, при выполнении условий ![]() происходит разрушение связей без продвижения вершины трещины и размер концевой зоны сокращается, стремясь к критическому значению для данного уровня нагрузки. При выполнении условий
происходит разрушение связей без продвижения вершины трещины и размер концевой зоны сокращается, стремясь к критическому значению для данного уровня нагрузки. При выполнении условий ![]() положения вершины трещины и концевой зоны не будут изменяться.
положения вершины трещины и концевой зоны не будут изменяться.
На основании полученных результатов на рис. 2 в случае жесткого включения при ![]() построены графики зависимости критической нагрузки
построены графики зависимости критической нагрузки ![]() от расстояния
от расстояния ![]() для обоих концов трещины, вдоль оси абсцисс (кривая 1 соответствует левому концу) при
для обоих концов трещины, вдоль оси абсцисс (кривая 1 соответствует левому концу) при ![]()
Штриховой линией для сравнения показана зависимость ![]() при отсутствии включений и покрытий (материал включения, покрытия и связующего одинаков) при той же геометрии трещин, вычисленная по описанной методике. Там же штрихпунктиром представлена зависимость в случае абсолютно гибкого включения (отверстия ничем не заполнены). Для любого упругого включения картина напряженного состояния будет занимать промежуточное положение между этими двумя предельными случаями.
при отсутствии включений и покрытий (материал включения, покрытия и связующего одинаков) при той же геометрии трещин, вычисленная по описанной методике. Там же штрихпунктиром представлена зависимость в случае абсолютно гибкого включения (отверстия ничем не заполнены). Для любого упругого включения картина напряженного состояния будет занимать промежуточное положение между этими двумя предельными случаями.
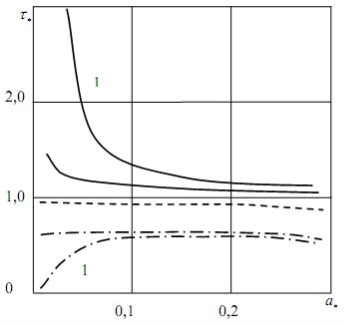
Рис. 2. Зависимости распределения критической нагрузки ![]() от расстояния
от расстояния ![]() от обоих концов трещины вдоль оси абсцисс
от обоих концов трещины вдоль оси абсцисс
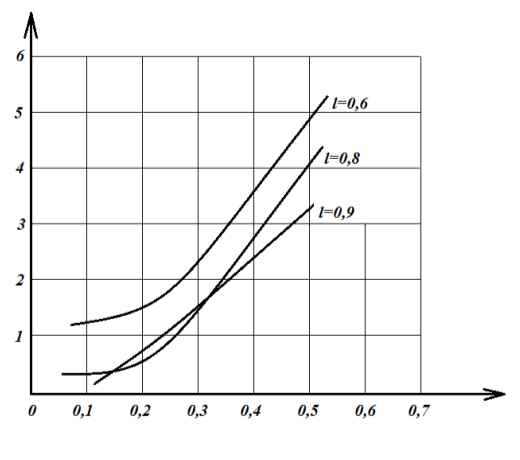
Рис. 3. Зависимости предельной нагрузки ![]() от длины трещины
от длины трещины ![]() для левого конца трещины
для левого конца трещины
![]()
![]()
![]()
![]()
![]()
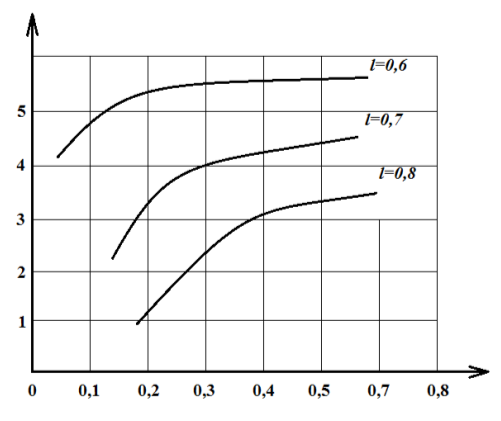
Рис. 4. Зависимости предельной нагрузки ![]() от длины трещины
от длины трещины ![]() для правого конца трещины
для правого конца трещины
На рис. 3–4 представлены графики зависимости предельной нагрузки ![]() от длины трещины. При расчетах было принято
от длины трещины. При расчетах было принято ![]()
Как видно, при некоторых значениях радиуса отверстия возможно устойчивое развитие системы трещин (их взаимное упрочнение). Проведенный параметрический анализ задачи показал, что концентрация напряжений около включений в связующем оказывает существенное влияние на развитие очень малых трещин. С ростом длины трещин с концевыми зонами это влияние затухает и уже при ![]() и
и ![]() им можно пренебречь, однако при этом начинается сказываться взаимодействие трещин. В зависимости от геометрических и физических параметров задачи наблюдается устойчивое развитие трещин с концевыми зонами. Наличие гибкого включения повышает коэффициент интенсивности напряжений, тогда как жесткие включения по сравнению с материалом связующего уменьшают его. Влияние включения особенно эффективно сказывается на близко расположенную вершину трещины.
им можно пренебречь, однако при этом начинается сказываться взаимодействие трещин. В зависимости от геометрических и физических параметров задачи наблюдается устойчивое развитие трещин с концевыми зонами. Наличие гибкого включения повышает коэффициент интенсивности напряжений, тогда как жесткие включения по сравнению с материалом связующего уменьшают его. Влияние включения особенно эффективно сказывается на близко расположенную вершину трещины.
Модель трещины с концевыми зонами позволяет исследовать закономерности распределения усилий в связях при различных законах деформирования, проводить анализ предельного равновесия трещин с учетом деформационного и силового критерий разрушения, а также прогнозировать критическую внешнюю нагрузку и трещиностойкость составного композита.
Заключение. Задача о трещины продольного сдвига в композитах с двоякопериодической структурой решена впервые.
Анализ критического равновесного состояния в композите с двоякопериодической структурой, при котором появляются трещины, сводится к параметрическому исследованию объединенной алгебраической системы (12), (20)—(24) и критерия появления трещины (26) при различных законах деформирования связей, упругих постоянных материалов и геометрических характеристиках композита. Непосредственно из решения полученных алгебраических систем определяются касательные напряжения в связях и сдвиг берегов зон предразрушения. Полученные соотношения позволяют исследовать трещинообразование в составном теле при продольном сдвиге.
Литература:
1. Болотин, В. В. Механика зарождения и начального развитияусталостных трещин / В. В. Болотин // ФХММ.–1986.–Т. 22, № 1.–С. 18–23.
2. Yang, Q. Cohesive models for damage evolution in laminated composites /Q. Yang, B. Cox //International Journal of Fracture.–2005.–Vol. 133, Issue 2.–Pp. 107–137.
3. Lipperman, F. Nucleation of cracks in two»dimensional periodic cellular materials /F. Lipperman, M. Ryvkin, M. B. Fuchs //Computational Mechanics.– 2007.–Vol. 39, Issue 2.–Pp. 127–139.
4. Gutkin, M.Yu. Effect of inclusions on heterogeneous crack nucleation in nanocomposites / M.Yu.Gutkin, I. A. Ovid’ko, N. V. Skiba //Physics of the Solid State.–2007.–Vol. 49, Issue 2.–Pp. 261–266.
5. Гольдштейн, Р. В. Моделирование трещиностойкости композиционных материалов / Р. В. Гольдштейн, М. Н. Перельмутер // Вычисл. мех.сплош. сред.–2009.–Т. 2,№ 2.–С. 22–39.
6. Кластеро–и трещинообразование в композитах / Е. В. Новиков [и др.] // Международный технико–экономическийжурнал.–2012.–№ 5.–С. 96–99.
7. Chen, Z. Estimation of the Stress State Within Particles andInclusions and a Nucleation Model for Particle Cracking /Z. Chen, C. Butcher //Micromechanics Modelling of Ductile Fracture: Solid Mechanics and Its Applications.–2013.–Vol. 195.–Pp. 223–243.
8. Мирсалимов, В. М. Разрушение упругих и упругопластических тел с трещинами / В. М. Мирсалимов.–Баку: Элм,1984.–124 с.
9. Ван ФоФы, Г. А. Теория армированных материалов с покрытиями / Г. А. Ван ФоФы.–Киев: Наук.думка, 1971.–236 с.
10. Лехницкий, С. Г. Кручение анизотропных стержней /С. Г. Лехницкий.–М.: Наука, 1971.–240 с.
11. Каландия, А. И. Математические методы двумерной упругости /А. И. Каландия.–М.: Наука, 1973.–304 с.
12. Мирсалимов, В. М. К решению задачи механики контактного разрушения о зарождении и развитии трещины со связями между берегами во втулке фрикционной пары /В. М. Мирсалимов //ПММ.–2007.–Т. 71, вып. 1.–С. 132–151.
13. Мирсалимов, В. М. Неодномерные упругопластические задачи /В. М. Мирсалимов.–М.: Наука, 1987.–256 с.
14. Ильюшин, А. А. Пластичность /А. А. Ильюшин.–М. Логос. 2004.–376 с.
15. Панасюк, В. В. Механика квазихрупкого разрушения материалов /В. В. Панасюк.–Киев:
16. Zolgharnein, E. Nucleation of a crack under inner compression of cylindrical bodies / E. Zolgharnein, V. M. Mirsalimov //ActaPolytechnicaHungarica.–2012.–Vol. 9, No. 2.–Pp. 169–183.
17. Vaghari, A. R. Nucleation of a crack in a perforated heat–releasing material with temperature dependent elastic properties /A. R. Vaghari, V. M. Mirsalimov //J. of Applied Mechanics and Technical Physics.–2012.–Vol. 53, No. 4.–Pp. 589–598.
18. Гасанов, Ф. Ф. Трещинообразование в перфорированном телепри продольном сдвиге /Ф. Ф. Гасанов//Механика машин, механизмов и материалов. –2013.–№ 2.–С. 46–51.
19. Искендеров, Р. А. Зарождение трещины при поперечном изгибе изотропной пластины, ослабленной периодической системой круговых отверстий /Р. А. Искендеров // Строительная механика инженерных конструкций и сооружений. –2013.–№ 3–С. 18–28.
20. Cherepanov, G. P. Methods of Fracture Mechanics /G. P. Cherepanov. Solid Matter Physics Series: Solid Mechanics and Its Applications.–1997.–Vol. 51, XIII.–322 p.
21. Mohammed, I. Cohesive zone modeling of crack nucleation at bimaterial corners / I. Mohammed, K. M. Liechti // Journal of the Mechanics and Physics of Solids.– 2000.–Vol. 48, Issue 4.–Pp. 735–764.
22. Yang, B. Examination of free»edge crack nucleation around an open hole in composite laminates / B. Yang // International Journal of Fracture.–2002.–Vol. 115, Issue 2.–Pp. 173–191. Наук.думка, 1991.–416 с.







