Статья опирается на результаты работы [1]. Приводятся ограничения, которым должны удовлетворять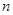 
- размерность пространства и
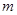- количество векторов, составляющих фрейм, при которых существуют равноугольные жёсткие фреймы. Описывается алгоритм построения равноугольных жёстких фреймов на основе сигнатурных матриц. Приводятся результаты построения равноугольных жёстких фреймов с использованием представленного алгоритма для случая 
.
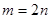Используем стандартное скалярное произведение 
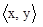векторов из 
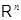и норму 
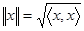. Система векторов 
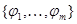из 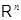называется равноугольной, если
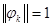при всех 
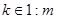и 
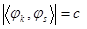при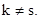 
Здесь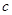 
- фиксированное число. Нас интересует случай 
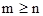. В докладе [2] выяснено, при каком значении 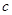равноугольная система является жёстким фреймом. Справедливо
ПРЕДЛОЖЕНИЕ 1. Равноугольная система является жёстким фреймом тогда и только тогда, когда
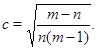
Необходимое и достаточное условия существования равноугольного жёсткого фрейма
К сожалению, равноугольные жёсткие фреймы существуют не для всех пар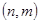 
. Чтобы выяснить для каких существуют, а для каких - нет, нам придётся проделать некоторые построения.
Пусть 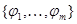- равноугольный жёсткий фрейм в , 
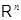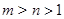. Из столбцов 
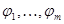составим матрицу 
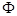размера 
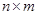. По критерию жёсткого фрейма
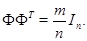
Рассмотрим теперь матрицу Грама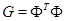 
. Для её элементов в силу равноугольности имеем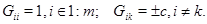 
Поскольку 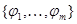- жёсткий фрейм, то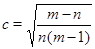 
Отсюда, в частности, следует, что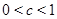 
. Кроме того, справедливо равенство
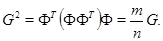(1)
Рассмотрим матрицу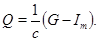 
У неё 
, 
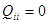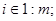
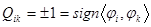при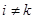 
. Вычислим матрицу 
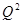с учётом равенства (1):
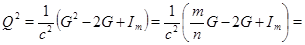
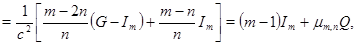(2)
где
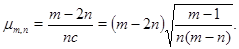(3)
Из равенства (3) при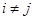 
получим 
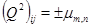, откуда следует, что 
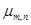является целым числом. Это одно из необходимых условий существования равноугольного жёсткого фрейма.
Чтобы сформулировать необходимое и достаточное условие введём понятие сигнатурной матрицы.
ОПРЕДЕЛЕНИЕ 1. Симметричная матрица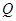 
размера 
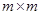называется сигнатурной, если
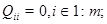
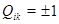при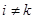
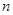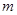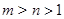ТЕОРЕМА 1. Для того чтобы при данных и , , существовал равноугольный жёсткий фрейм, необходимо и достаточно, чтобы выполнялись условия:
1. число 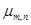, определённое равенством (3) , является целым;
2. существует сигнатурная матрица Q такая, что
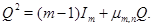(4)
Доказательство. Необходимость установлена выше. Докажем достаточность проще, чем в работе [1]. Выведем матрицу
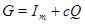, где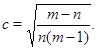
У неё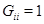 
, 
; 
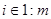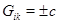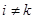при . Вычислим 
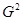. С учётом (4) элементарными вычислениями получим
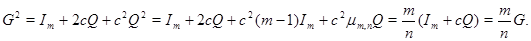
Из равенства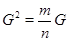 
следует, что матрица 
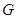имеет собственные числа 
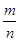и 
. Обозначим кратность первого числа через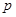 
, тогда имеет кратность 
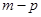. Поскольку 
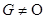, то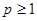 
.
Тогда симметричную матрицу G можно представить в ви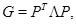де 
где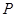 
- ортогональная матрица, 
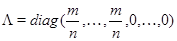. Рассмотрим матрицу 
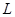размера 
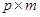вида
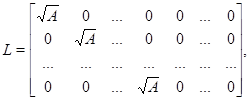
где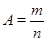 
. Тогда 
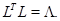Для матрицы 
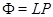справедливо равенство
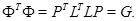
Столбцы 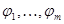матрицы 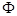образуют равноугольную систему. Действительно, 
; 
.
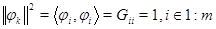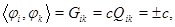
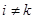Кроме того, матрицы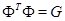 
и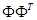 
имеют одинаковые ненулевые собственные числа. Следовательно, матрица 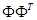имеет только одно собственное число 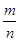кратности 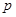и, значит,
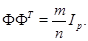
По определению система 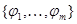- жёсткий фрейм в 
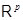. Но тогда, по предложению 1, справедливо равенство
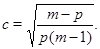
Отсюда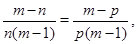 
то есть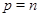 
. Построили равноугольный жёсткий фрейм в 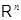. Теорема доказана. 
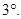Оценки числа элементов равноугольного жёсткого фрейма
В докладе [2] приведено простое доказательство следующего предложения.
ПРЕДЛОЖЕНИЕ 2. Пусть 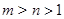. Если 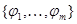- равноугольный жёсткий фрейм в 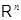, то
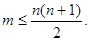(5)
Это неравенство в сочетании с теоремой 1 позволяет установить другое ограничение на число .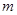
ПРЕДЛОЖЕНИЕ 3. Пусть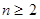 
, 
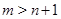. Если 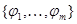- равноугольный жёсткий фрейм в 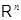, то
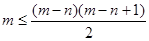. (6)
Доказательство. По теореме 1 фрейму 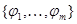соответствует сигнатурная матрица 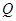, удовлетворяющая уравнению
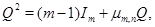
где 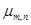задано формулой (3). Заменим в этой формуле 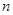на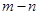 
. Отметим, что
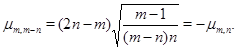
Поэтому сигнатурная матрица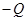 
удовлетворяет равенству
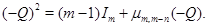
Поскольку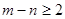 
, 
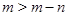, то по теореме 1 существует равноугольный жёсткий фрейм 
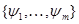в пространстве 
.
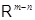По предложению 2 справедливо неравенство (6). Предложение доказано.
Неравенства (5) и (6) вместе с требованием целочисленности 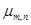позволяют отбросить многие пары 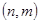, для которых заведомо не существуют равноугольные жёсткие фреймы. Приведём ряд примеров для случая 
, .
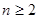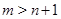ПРИМЕР 1.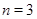 
. Неравенство (5) имеет вид 
.
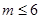При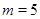 
не выполнено неравенство (6).
При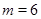 
оба неравенства (5) и (6) превращаются в равенства. Возникает подозрение, что в случае 
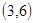есть равноугольный жёсткий фрейм. В явном виде он выписан в докладе [2].
ПРИМЕР 2.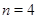 
. Неравенство (5) имеет вид 
.
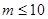При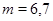 
не выполнено неравенство (6).
При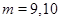 
число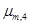 
не целое.
При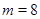 
выполнены неравенства (5) и (6) и число 
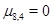. Как будет показано далее, в случае 
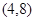равноугольный жёсткий фрейм не существует.
Нахождение равноугольных жёстких фреймов в случае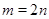 
методом перебора сигнатурных матриц
Случай 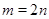является довольно исключительным. При 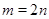число 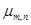равно нулю и по теореме 1 для существования равноугольного жёсткого фрейма необходимо и достаточно существование сигнатурной матрицы 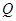, удовлетворяющей равенству
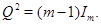(7)
По определению сигнатурная матрица 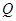симметрична. Поэтому если через 
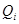обозначить 
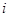-ю строку 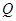, то условие (7) запишется в виде
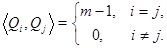
Условие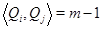 
выполняется автоматически так как каждая строка 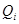содержит один ноль и 
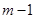элементов, равных 
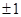. Так что нужно только обеспечить ортогональность строк: 
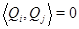при .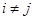
Отметим, что если сигнатурная матрица 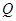удовлетворяет (7), то после умножения 
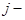го столбца и строки 
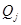на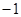 
снова получим решение (7). Поэтому можно считать, что в первой строке 
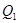стоят единицы: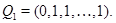 
Далее можно пытаться строить строки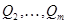 
так, чтобы каждая строка была ортогональна предыдущим строкам.
При 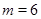это удаётся проделать вручную и получить матрицу
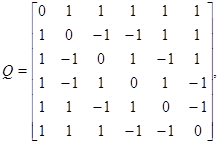
удовлетворяющую равенству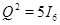 
(этот же пример приведён в [1]).
При 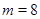можно с помощью компьютерной программы перебирать элементы 
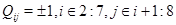. Всего 21 элемент и 
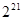комбинаций 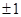. Полный перебор приводит к выводу, что сигнатурная матрица, удовлетворяющая равенству 
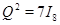не существует, и, следовательно, не существует равноугольный жёсткий фрейм при 
.
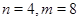При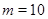 
программа нашла сигнатурную матрицу
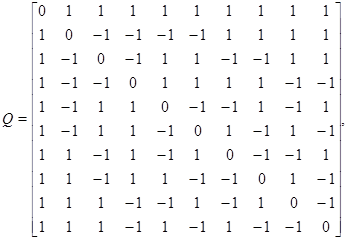
удовлетворяющую равенству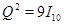 
.
Далее с помощью компьютерной системы Maple 9.5 проводим символьные вычисления, указанные в доказательстве теоремы 1: строим матрицу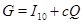 
, находим её ортогональное разложение 
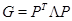, строим матрицу 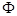размера 
:
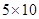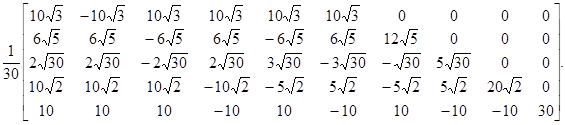
С помощью Maple 9.5 легко проверяются равенства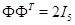 
и 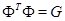. Тем самым столбцы матрицы 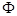образуют равноугольный жёсткий фрейм в 
.
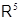Точно также программа нашла сигнатурные матрицы пр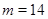и 
и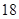 
, а с помощью Maple 9.5 построены равноугольные жёсткие фреймы в 
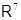и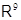 
.
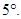Необходимое условие существования равноугольного жёсткого фрейма при 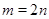. Это условие установлено в работе [3].
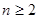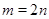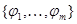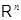ТЕОРЕМА 2. Пусть , . Если существует равноугольный жёсткий фрейм в , то 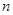- нечётное и 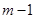является суммой двух квадратов целых чисел.
В качестве иллюстрации приведём примеры.
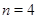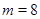При чётном и равноугольный жесткий фрейм не существует.
При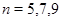 
числа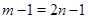 
являются суммами квадратов двух целых чисел:
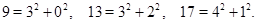
В случаях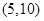 
, 
, 
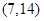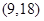существование равноугольных жёстких фреймов подтверждается расчётами (см. п. 4).
При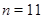 
, 
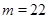число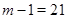 
не представимо в виде суммы двух квадратов и по теореме 2 равноугольный жёсткий фрейм не существует.
Литература:
1. Holmes R. B., Paulsen V. I. Optimal frames for erasures // Linear Algebra Appl. 2004. V. 377. P. 31-51.
2. Малозёмов В. Н., Певный А. Б. Равноугольные жёсткие фреймы // Проблемы математического анализа. 2009. Выпуск 39. С. 3-25.
3. Sustik M. A., Tropp J. A., Dhillon I. S., Heath R. W. On the existence of equiangular tight frames // Linear Algebra Appl. 2007. V. 426. P. 619-635.
