Исследование статической устойчивости Навоийской ТЭС методом функций Ляпунова в квадратичной форме



Исследование устойчивости электрических систем базируется на известных классических положениях общей теории устойчивости движения [1]. Статическая устойчивость электрических систем (устойчивость при малых возмущениях) исследуется на основе методов, которые базируются на анализе дифференциальных уравнений первого (линейного) приближения, получивших плодотворное применение и развитие в теории автоматического регулирования [1–4,6]. Она позволяют наиболее просто раскрыть сущность проблемы, сформулировать наиболее характерные ее особенности, выделить факторы, имеющие первостепенное и решающее значение. Применительно к энергосистеме устойчивость в малом — это устойчивость установившегося (стационарного) движения, которое подвергается непрерывному воздействию малых возмущений — включение и отключение небольших нагрузок, коммутации в распределительных сетях низкого напряжения, различного рода вибрации, изменение температуры, давления и т. п.

Проверка статической устойчивости энергосистем заключается в определении возможности существования устойчивого режима при заданных значениях параметров энергосистемы (определяемых составом работающего оборудования и электрической сети), режиме генерирующих источников, нагрузках узловых точек и настройке автоматических устройств регулирования режима.

Важно, однако, не только выяснить существование и устойчивость рассматриваемого режима, но и определить, насколько близок этот режим к предельному если статическая устойчивость обеспечивается, или определить, каким образом должны быть изменены схема и регулируемые параметры режима с тем, чтобы ввести режим в допустимую область, если необходимый запас статической устойчивости не обеспечивается.

Отсюда следует, что анализ статической устойчивости энергосистемы должен включать следующие задачи: проверку статической устойчивости заданного режима, определение предельно допустимых режимов по статической устойчивости, определение области статической устойчивости в пространстве регулируемых (независимых) параметров и выбор их значений. Перечисленные задачи обычно решаются в настоящее время для детерминированных условий. Обычно анализ статической устойчивости сложной системы в большинстве случаев осуществляется в предположении отсутствия самораскачивания в энергосистеме, считая, что это условие обеспечено соответствующей настройкой автоматических регуляторов. В этом случае задача упрощается и сводится к проверке апериодической статической устойчивости системы. Проверка апериодической устойчивости обычно заключается в определении знака свободного члена характеристического уравнения, получаемого на основе системы линейных дифференциальных уравнений первого приближения [4].

Если в системе выполняются условия собственно статической (апериодической) устойчивости, то нарушение устойчивой работы возможно только за счет динамических свойств системы. Оно обычно проявляется в виде нарастающих колебаний (самораскачивание).

Классический метод малых колебаний, основанный на уравнениях первого (линейного) приближения, пока остается одним из наиболее эффективных методов решения прикладных инженерных задач устойчивости энергосистем при малых возмущениях. Основным достоинством метода являются его простота и наглядность. Однако реально метод применим, если исследуемая система невысокого порядка и размерности. Это обстоятельство в значительной мере ограничивает возможности метода для решения задач устойчивости многомашинных регулируемых энергосистем в полном объеме, так как, такие системы описываются уравнениями весьма высокого порядка.

При полном анализе статической устойчивости в качестве условно-эталонной принимается линеаризованная в окрестности рассматриваемого состояния модель ЭЭС, которая в случае одного синхронного генератора включает: упрощенные уравнения Парка—Горева для описания генератора с учетом обмотки возбуждения и не менее двух демпферных контуров на роторе; уравнения системы возбуждения с АРВ 5÷7-го порядков, учитывающие элементы с постоянными времени до нескольких сотых секунды; уравнения нагрузки с учетом ее структуры. Электромагнитные переходные процессы в элементах сети не учитываются, мощность турбины обычно предполагается постоянной [2]. Очевидно, что порядок систем уравнений, подлежащих решению с увеличением количества учитываемых генераторов резко возрастает, что исключает возможность аналитического исследования и создает трудности применения известных алгебраических и частотных методов [1–3]. Система моделей для расчета статической устойчивости, включая условно-эталонную и упрощенные, их анализ и обоснование рассмотрены в [4].

При этом необходимо отметить, что для полного анализа статической устойчивости используются методы: прямого расчета спектра матрицы системы, оценки отсутствия собственных чисел в правой полуплоскости по косвенным критериям, динамического моделирования [1,2].

Сложность решаемой задачи известными алгебраическими и частотными методами общеизвестны, к тому же они дают только необходимые условия устойчивости, предполагая выполнения достаточных условий статической устойчивости. Здесь можно привести широко применяемый пример исследования апериодической устойчивости в предположении отсутствия других видов статической устойчивости (самораскачивания и самовозбуждения).

Одним из наиболее плодотворных является прямой метод Ляпунова, требующий подбора специальных функций (функций Ляпунова) и вычисления их производных с учетом уравнений возмущенного движения (последние должны быть известны в форме Коши). Сложность этого метода, в рамках которого формулируются достаточные условия устойчивости и неустойчивости в виде соответствующих теорем, общеизвестна. Она связана с тем, что в общем случае нет общих методов построения функций Ляпунова. Поэтому в инженерной практике применение прямого метода Ляпунова ограниченно. Кроме того, решения, получаемые указанным методом, не всегда достаточно характеризуют систему с прикладной точки зрения, так как разные в этом отношении особые случаи могут оцениваться одинаково. Вместе с тем существует функция Ляпунова в квадратичной форме, обеспечивающее в случае применения для линейных автономных систем и необходимые и достаточные условия устойчивости. Возможности современных вычислительных машин, оперирующих миллиардными операциями в секунду открывают большие возможности применения функций Ляпунова в квадратичной форме для решения n(n+1)/n уравнений [/8].

Прямой метод Ляпунова, применяемый для исследования устойчивости отмечено динамических систем, в том числе электроэнергетических, как было отмечено в общем случае предполагает нахождение специальной знакоопределенной функции V(х, х, х,…х) переменных состояния, производная которой , взятая в силу системы дифференциальных уравнений, описывающих динамику системы, должна быт знакопостоянной противоположного знака с V или тождественно равна нулю или же строго знакоопределенной противоположного знака с V. При этих условиях система соответственно устойчива или асимптотически устойчива [7,6]. Построение V в общем случае выполняется методом проб. Вместе с тем для линейной автономной системы функция V строится в квадратичной форме от переменных состояния [9]. Существованием V в этом случае обеспечиваются одновременно необходимые и достаточные условия равномерной асимптотической устойчивости в целом [7,9].

Рассмотрим линейную стационарную систему

= A X, (1)

где A =- квадратная постоянная матрица;

Х -n — мерный вектор — столбец с координатами х, х,…, х

Определим, следуя Ляпунову, для этой системы функцию V в квадратичной форме

V==, i, j= 1, 2,..., n; (2)

здесь Q- пока не известная квадратная матрица коэффициентов квадратичной формы; - транспонированный Х (вектор-строка).

Полная производная от V по времени в силу (2) будет

QX+QX=QX+QAX= (Q+QA) X (3)

Потребуем, чтобы V удовлетворяла условию

- W, (4)

где W- произвольно задаваемая квадратичная форма переменных состояния.

Обозначим

Q+ QA= — С. (5)

Последнее уравнение ставит в соответствие всякой симметричной матрице Q матрицу С и наоборот, причем это соответствие линейно. Элементы матрицы Q определяются из (5) решением уравнений, где n- число уравнений. Если задаться положительно определенной симметричной матрицей С (при этом найденная из (5) матрица Q окажется также положительно определенной), то ввиду линейности и стационарности системы (1) получим согласно теореме Ляпунова асимптотическую устойчивость ее положения равновесия [7, 9]. При этом условия устойчивости должны быть строго эквивалентными полученным из критериев Рауса — Гурвица [5,9]

Исследуем статическую устойчивость простейшей нерегулируемой= const) системы генератор — линия — шины при U = const с учетом переходных процессов в обмотке возбуждения. После разложения правой части уравнения движения ротора синхронной машины в ряд Тейлора в окрестности точки получим [10]

+ = — — (6)

Уравнение переходного процесса в обмотке ротора будет

= - (7)

Учитывая, что

= + U (8)

имеем

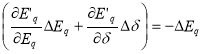(9)

При этом характеристическое уравнение имеет вид:

где — коэффициенты характеристического уравнения, - Э. Д. С возникаюший под действией регулятора или возмущения, - переходное индуктивное сопротивление, - переходная Э. Д. С., - угол устойчивости. Основные обозначение обще принятие.

Функцию Ляпунова построим следующим образом.

Обозначив

= , = ,

, = ,

из (6)-(9) получим

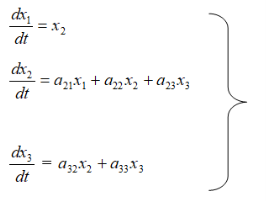(10)

где

, = — , = — , = U sin

= — , = , , ,

— ).

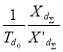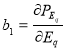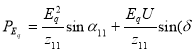Матрица коэффициентов системы (1) будет

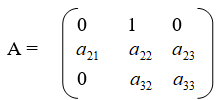
Функция Ляпунова в нашем случае при n = 3 согласно (11) запишется так:

V = Q X = (11)

Из (11) можно получит V в силу (10) в соответствии с (3) — (5). Зададимся С в виде единичной матрицы. Тогда

W =. (12)

Приравнивая коэффициенты и (i, j=1, 2, 3) в выражениях для V и W, получаем систему уравнений

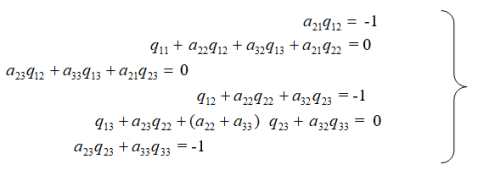13

откуда и определяем = 1, 2, 3)

Таким образом, матрица коэффициентов квадратичной формы (11) согласно (2)

имеет вид

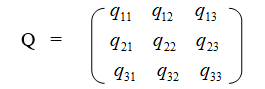
Мы задались определенно отрицательной производной W (положительно определенной симметричной С). Если при этом условия положительной определенности матрицы Q квадратичной формы (11) будут удовлетворены, то, очевидно, условия асимптотической устойчивости положения равновесия системы (10) будут обеспечены.

Для положительной определенности квадратичной формы (11) согласно критерию Сильвестера (см. [9]) необходимо и достаточно, чтобы главные диагональные миноры матрица Q были положительными:

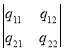>0, 0, 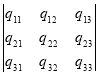>0. (14)

Эти условия рассмотрены [5] и показано их нарушение при нарушении положительности

=>0 (15)

0 (16)

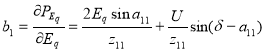 0,

т. е. когда

 . (17)

Другими словами, из условий положительности (14) вытекает условия нарушения статической устойчивости нарушение. Условие (15) — (17), как известно, определяют нарушение статической устойчивости системы- т. е. апериодическое нарушение, самораскачивание, и самовозбуждение в системе.

В случае выполнения условий (14), и соответственно (15) — (17) в системе, получающей «малые» возмущения, обеспечивается асимптотическая устойчивость положения равновесия (10).

Таким образом, условия нарушения статической устойчивости электрических систем (15) — (17), полученные вторым методом Ляпунова, совпадают с ранее найденными на основе обобщенных условий Рауса — Гурвица [10].

Ниже приведены характер изменения определителей Ляпунова, коэффициентов характеристического уравнение и определителей Гурвица рис.1, 2

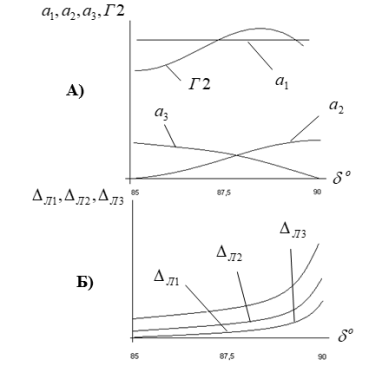
Рис. 1. Характер изменения коэффициентов и определителей Гурвица хактеристического уравнения (А) определителей матричного уравнения Ляпунова (Б)

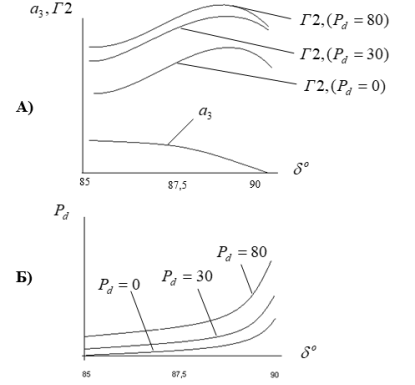
Рис. 2. Характер изменения коэффициентов и определителей Гурвица хактеристического уравнения Ляпунова (Б) в случае изменения коэффициента демпфирования

Все условия нарушения статической устойчивости электрической системы содержатся в первом элементе матрицы Q и, как выявлено, это положение не зависит от сложности системы, в то же время коэффициенты характеристического уравнения и определители Гурвица изменяются произвольно. Анализ показал, что если непрерывно увеличить коэффициент усиления АРВ, то при положительности коэффициентов характеристического уравнения определитель Гурвица проходит через нулевое значение, в то время как определители матричного уравнения Ляпунова (14) одновременно все устремляются в бесконечность. На рис.3 показано изменение коэффициентов и определителей Гурвица системы, состоящей из трех генераторов описываемой уравнением четвертого порядка при наличии на синхронном генераторе АРВ пропорционального типа. Утяжеление проводится постепенным увеличением передаваемой мощности при заданном коэффициенте усиления по каналу напряжения, равным K=10 ед. Параметры системы: U=1.05; T=8 c; T =1.68 c; T = 0.3 c; x= 2.1; x=0.3; x=0.4. Обозначения: a- коэффициенты характеристического уравнения; -определители матрицы Гурвица; -миноры матрицы коэффициентов квадратичной формы.

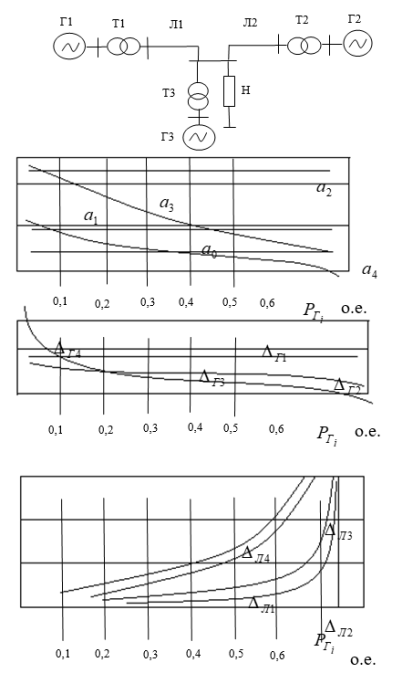
Рис. 3.

Нарушение устойчивости происходит вследствие самораскачивания гораздо раньше, чем «сползание» системы. Аналогичные условия нарушения устойчивости получены и для случая, когда на СГ используется автоматический регулятор возбуждения сильного действия. Здесь же приведены зависимости миноров матрицы Q от угла, которые показывают нарушение устойчивости при том же значении угла, что и для предпоследнего определителя Гурвица. Анализ приведенных результатов показал, что изменение коэффициентов и миноров матрицы квадратичной формы функции Ляпунова с утяжелением режима имеет одинаковый характер, в то время как поведение коэффициентов характеристического уравнения и определителей Гурвица совершенно разное. Учитывая, что первый элемент матрицы Q содержит всю информацию о поведении электрической системы, что подтверждено аналитически и расчетом системы разной сложности, анализ устойчивости положения равновесия можно упросить исследованием q и рассматривать это как практический критерий статической устойчивости, дающий необходимые и достаточные ее условия.

Расчетный анализ основан на позиционной модели электрической системы, которая учитывает изменения взаимных углов генераторов и поэтому требуется решение систем линейных уравнений высокого порядка. Расчетную процедуру можно упросить, а получаемые результаты усилить совместным применением данного метода и метода уравнений узловых напряжений [11]. При этом для каждой точки исследуемого режима электрической системы, устойчивость которой проверяется, по УУН находится напряжение узлов и при U = пост последовательно проверяется положительность матрицы квадратичной формы Ляпунова для генерирующих узлов и узлов, содержащих вращающиеся машины. По существу задача сводится к исследованию схемы генератор — шины с постоянным напряжением, которая в практических расчетах описывается уравнением не более 4–10 порядка. При этом строго и однозначно будут решаться вопросы выбора параметров АРВ, АРС; появляется также возможность учета нелинейностей (линеаризованных) типа зоны нечувствительности, насыщения и др.

Таким образом, современное состояние и перспективы развития ЦВМ и наличие эффективных методов линейной алгебры создают все условия для использования метода функций Ляпунова в квадратичной форме для изучения статической устойчивости электрической системы. При практических расчетах для уменьшения вычислительной процедуры статическую устойчивость электрической системы в позиционной идеализации целесообразно исследовать по характеру изменения первого элемента матрицы квадратичной формы функции Ляпунова, доставляющей необходимые и достаточные условия ее устойчивости.

Наиболее эффективно совместное применение функций Ляпунова в квадратичной форме и уравнений узловых напряжений.

Литература:

1. Автоматизация диспетчерского управления в электроэнергетике бод ред. Ю. Н. Руденко и В. А. Семенова М. Издательство 2000, 648 с.
2. Автоматизации управления энергообъединениями. Под род. С. А. Совалова. М. Энергии,1979, 431с.
3. Е. И. Ушаков Статическое устойчивость электрических систем. Под ред Ю. Н. Руденко Новосибирск, Наука, 1988, 272с
4. О. М. Костюк. Элементы теории устойчивости энергосистем. Киев, Наукова душка, 1983, 293 с
5. К. Р. Аллаев. Исследование статической устойчивости электрических систем методом функций Ляпунова квадратичной форме. Т. Фан, С. Т. Н. 1973.
6. Н. Н. Иващенко. Автоматическое регулирование. Теория и элементы системы. М, Машиностроения. 1973, 606с
7. А. М. Ляпунов. Общая задача об устойчивости движения. М — Л. Гость. Издательство тех- теор. аит, 1950.
8. О. С. Аладышев и др. СуперЭВМ: области применения и требования к производительности. М. Извести вузов, Электроника, 2004, N1.
9. Ф. Р. Гантмахер. Теория матриц. М. Наука, 1967.
10. В. А. Веников. Переходные электромеханические процессы в электрических системах. М. Высшая школа,1984.
11. Х. Ф. Фазылов. Методы режимных расчетов электрических систем. Т. Фан, 1968, 98с