Рассматривается вязкоупругая цилиндрическая панель со сторонами и , радиусом кривизны срединной поверхности , обтекаемой сверхзвуковым потоком газа со скоростью .

Интегральную модель, связывающую напряжения в срединной поверхности , , и деформации , , , согласно модели Больцмана-Вольтерра примем в виде [1]

, (1)

где — модуль упругости; — коэффициент Пуассона; символ (xy) указывает, что остальные соотношения получаются круговой перестановкой индексов; — интегральный оператор с ядром релаксации .

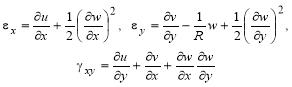Геометрическую модель, связывающую деформации в срединной поверхности , , и перемещения , , , примем в виде [2]

(2)

Геометрические соотношения же между деформациями и угловыми перемещениями , примем в виде [2]:

(3)

где , , определяются из соотношений (2).

С учетом (1) и (3) изгибающие, крутящие моменты , , и поперечные силы , имеют вид

(4)

где (Миндлин), 2/3 (Уфлянд) и 5/6 (Рейсснер) [3].

Подставив (1), (3) и (4) в уравнения [2] получим следующую систему уравнений:

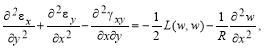
где .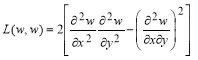

В случае линеаризированного течения газа вдоль панели, по которой распространяются упругие волны, нормальная составляющая скорости имеет вид [4]

и, следовательно, избыточное давление приобретает вид [4]

Здесь æ — показатель политропы, и — давление и скорость в невозмущенном газе.

Далее введя функцию напряжений в срединной поверхности в виде [2]

для определения поперечного прогиба , функции напряжений и угловых перемещений , , получим систему уравнений типа Кармана, вида

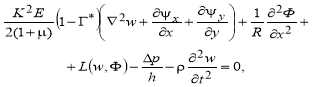(7)

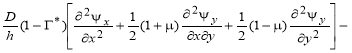
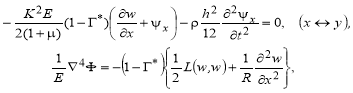
где .

Пусть все стороны вязкоупругой цилиндрической панели шарнирно оперты. Удовлетворяя граничным условиям задачи, выберем выражения для прогибов и угловых перещений на основе многочленной аппроксимации в виде:

(8)

Подставляя первое выражение (8) в четвертое уравнение системы (7) и приравнивая в обеих частях этого уравнения коэффициенты при одинаковых гармониках тригонометрических функций, находим функцию усилий [5]:

(9)

где коэффициенты , , , , определяются из [5];

, .

Подставляя (8) и (9) в (7) и выполняя процедуру Бубнова-Галеркина, после введения следующих безразмерных величин

и сохранения прежних обозначений, относительно неизвестных , , получим:

,

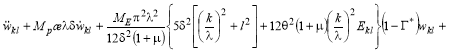
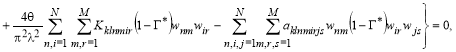
, (10)

,

где ; ; ; - число Маха [4]; ; _k=1, если k нечетное, если же k четное или равно 0, то _k=0 и _k=0; коэффициенты , определяются из [5].

Изучено влияние вязкоупругих свойств материала панели на её динамическое поведение. На рис.1 представлена зависимость прогиба от времени срединной точки упругой (А=0 — кривая 1) и вязкоупругих панелей (А=0.03, 0.05, 0.07 — кривые 2,3,4).

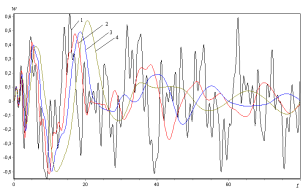
Рис. 1. Зависимость прогиба от времени при A=0 (1); 0.03 (2); 0.05 (3); 0.07 (4)

Как видно из рисунка, учет вязкоупругих свойств материала панели приводит к затуханию колебательного процесса.

Также исследовано влияние реологического параметра . Анализ полученных здесь результатов показывает, что уменьшение значения этого реологического параметра приводит к интенсивному уменьшению амплитуды и сдвигу фаз вправо, следовательно, к уменьшению частоты колебаний.

Литература:

1. Колтунов М. А. Ползучесть и релаксация. — М.: Высшая школа, 1976. — 276 с.
2. Вольмир А. С. Нелинейная динамика пластинок и оболочек. — М.: Наука, 1972. — 432 с.
3. Амбарцумян С. А. Общая теория анизотропных оболочек. — М.: Наука, 1974. — 448 с.
4. Болотин В. В. Неконсервативные задачи теории упругой устойчивости. — М.: Физматгиз, 1961. — 340 с.
5. Эшматов Х. Интегральный метод математического моделирования задач динамики вязкоупругих систем: Дис... на соис. учен. степ. док. техн. наук. — Киев, 1991. — 337 с.