I.Introduction
Laplace transform is an integral transform method which is particularly useful in solving linear ordinary differential equations. It finds very wide applications in various areas of physics, electrical engineering, control engineering, optics, mathematics and signal processing.
In order for any function to be Laplace transformable, it must satisfy the following Dirichlet conditions [1]:
– ![]() must be piecewise continuous which means that it must be single valued but can have a finite number of finite isolated discontinuities for
must be piecewise continuous which means that it must be single valued but can have a finite number of finite isolated discontinuities for ![]() .
.
– ![]() must be exponential order which means that f(t) must remain less than
must be exponential order which means that f(t) must remain less than ![]() as approaches
as approaches ![]() where S is a positive constant and
where S is a positive constant and ![]() is a real positive number.
is a real positive number.
If there is any function ![]() that satisfies Dirichlet conditions, then,
that satisfies Dirichlet conditions, then,
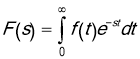 written as
written as ![]() is called the Laplace transformation of
is called the Laplace transformation of ![]() :
:
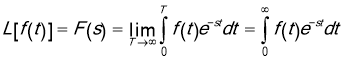
Here, ![]() can be either a real variable or a complex quantity.
can be either a real variable or a complex quantity.
The integral ![]() converges if
converges if 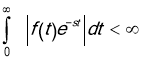 ,
, ![]() .
.
Some important properties of Laplace transform.
We would like to establish some properties of the Laplace transform for all functions that are piecewise continuous and have exponential order at infinity. Some of the very important properties of Laplace transforms are described as follows: [1] [2]
– Linearity
The Laplace transform of the linear sum of two Laplace transformable functions ![]() is given
is given
![]()
– Differentiation
If the function ![]() is piecewise continuous so that it has a continuous derivative
is piecewise continuous so that it has a continuous derivative ![]() of order
of order ![]() and a sectional continuous derivative
and a sectional continuous derivative ![]() in every finite interval
in every finite interval ![]() , then let,
, then let, ![]() and all its derivatives through
and all its derivatives through ![]() be exponential order
be exponential order ![]() as
as ![]() .
.
Then, the transform of ![]() exists when
exists when ![]() and has the following form:
and has the following form:
![]()
II.Laplace transform and convolutions.
Convolutions were originally introduced in Number Theory, but it was soon proved that it was also useful in Mathematical Analysis, because the discrete and continuous formulas were of the same structure, and the continuous formula also occurred naturally in solution formula. The convolution of two functions, ![]() and
and ![]() , defined for
, defined for ![]() , plays an important role in a number of different physical applications. [3].
, plays an important role in a number of different physical applications. [3].
Definition. Let
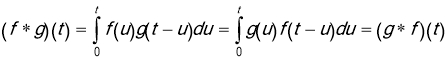
that is, the convolution is commutative.
One of the very significant properties possessed by the convolution in connection with the Laplace transform is that the Laplace transform of the convolution of two functions is the product of their Laplace transform. The following theorem, known as the Convolution Theorem, provides a way for finding the Laplace transform of a convolution integral.
Theorem [4]. If ![]() and
and ![]() are piecewise continuous for
are piecewise continuous for ![]() , and of exponential order at infinity then
, and of exponential order at infinity then
![]()
Thus, ![]() .
.
Proof. First, we show that ![]() has a Laplace transform. From the hypotheses we have that
has a Laplace transform. From the hypotheses we have that ![]() for
for ![]() and
and ![]() for
for ![]() . Let
. Let ![]() and
and ![]() . Then for
. Then for ![]() we have
we have
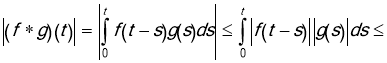
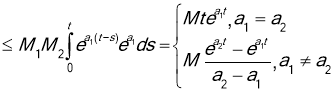
This shows that ![]() is exponential order at infinity. Since
is exponential order at infinity. Since ![]() and
and ![]() are piecewise continuous, the first fundamental theorem of calculus implies that
are piecewise continuous, the first fundamental theorem of calculus implies that ![]() is also piecewise continuous. Hence,
is also piecewise continuous. Hence, ![]() has a Laplace transform.
has a Laplace transform.
Next we have
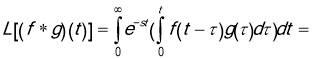
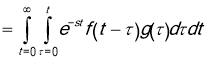
Note that the region of integration is an infinite triangular region and the integration is done vertically in that region. Integrating horizontally we find
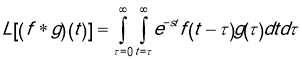
We next introduce the change of variables ![]() . The region of integration becomes
. The region of integration becomes ![]() ,
, ![]() . In this case, we have
. In this case, we have
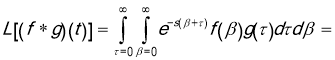
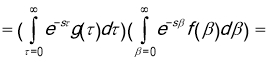
![]() .
.
Example. Use the convolution theorem to find the inverse Laplace transform of
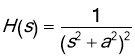
Solution. Note that
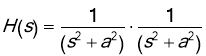
So, in this case we have, 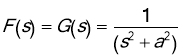 . Since
. Since 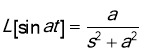 , we find
, we find 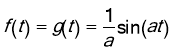 .
.
Thus,
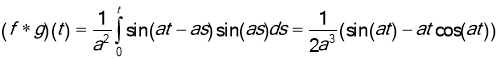 .
.
References:
- A. D. Poularikas, The Transforms and Applications Hand-book (McGraw Hill,2000), 2nd ed.
- M. J. Roberts, Fundamental of Signals and Systems (McGraw Hill, 2006), 2nd ed
- Leif Mejlbro, The Laplace Transformation I-General Theory, Leif Mejlbro & Ventus Publishing ApS,2010.
- Marcel B. Finan, Laplace Transforms: Theory, Problems, and Solutions. Arkansas Tech University.







