Перенос вещества в неоднородной пористой среде с учетом неравновесной адсорбции



Задачи переноса вещества и движения жидкости в макроскопически неоднородных пористых средах являются актуальной проблемой во многих отраслях техники и технологии. Наряду с экспериментальными, полевыми исследованиями математическое моделирование переноса вещества и движения жидкости в таких средах позволяет эффективно изучить основные характеристики процесса.

Адсорбция при переносе веществ в пористой среде значительно влияет на характеристики переноса. Предложен ряд моделей для описания адсорбции химических веществ на породы [1–3]. В работе [4] рассмотрена задача переноса загрязняющих веществ в пористой среде, состоящей из двух зон (с подвижной и неподвижной водой), с учетом явлений конвективного переноса, гидродинамической дисперсии, двухместной адсорбции и внутреннего диффузионного массопереноса между двумя зонами. Для описания массообмена между зонами использованы линейные и нелинейные кинетические уравнения [5, 4].

В данной работе рассматривается перенос вещества в цилиндрической пористой среде с центральной цилиндрической макропорой с учетом неравновесной адсорбции. Задача анализируется в диффузионной и кинетической постановке, описывающей перенос вещества из макропоры в цилиндрическую окружающую среду.

Так, рассматривается цилиндрическая пористая среда с цилиндрической макропорой в центре, т. е. область исследования задачи состоит из двух частей: 1) Макропористая среда (макропора), имеющая радиус (т. е. область ), с большими порами, характеризирующаяся относительно высокой пористостью и относительно большой скоростью жидкости в ней, 2) окружающая цилиндрическая микропористая среда (микропора), занимающая область , имеющая низкую (или нулевую) пористость и, соответственно, относительно низкую скорость потока (Рис.1) [6].

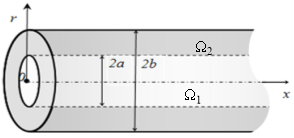
Рис.1. Цилиндрическая среда с цилиндрической макропорой.

Используем следующие соотношения [6]

, , , , , , , ,

где , — объемные доли макропоры и микропоры в единице объема среды, , — локальные коэффициенты пористости макропористой и микропористой сред, , — относительные коэффициенты пористости макропористой и микропористой сред, , — локальные плотности макропористой и микропористой сред, , - относительные объемные плотности двух сред.

В макропоре в одномерной постановке перенос вещества описывается уравнением [6]

,(1)

где - средняя объемная концентрация в , — концентрация адсорбированного вещества в макропоре, — коэффициент диффузии в макропоре, — средняя скорость распространения вещества в , , (м³/кг) — средние концентрации вещества и концентрации адсорбированного вещества в области , которые определяются из следующих соотношений

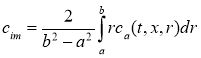,(2)

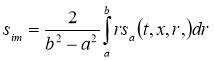,(3)

— локальная концентрация в , — локальный удельный объем адсорбированного вещества в единице массы , — время, — расстояние.

Распространение вещества в области описано уравнением диффузии с учетом адсорбции вещества

, .(4)

где — коэффициент эффективной диффузии в . Уравнение (4) дополняется условием непрерывности концентрации на общей границе микро- и макропористой сред

.(5)

В цилиндрической окружающей среде продольное распространение вещества не учитывается и внешняя граница () является непроницаемой для вещества

.(6)

В точке по всей площади поперечного сечения начиная с в среду поступает неоднородная жидкость с постоянной концентрацией вещества и со средней постоянной скоростью . Начальные и граничные условия принимаются в виде:

, (7)

, (8)

,(9)

, , (10)

.(11)

Кинетические уравнения неравновесной адсорбции используются в виде

,(12)

,(13)

,(14)

где — коэффициент характерного перехода времени от неравновесного к равновесной адсорбции.

Начальные условия для концентраций адсорбированных веществ, принимаются в виде

, (15)

, (16)

. (17)

Задача (1) — (17) решается методом конечных разностей [7].

Уравнение (1) после аппроксимации приводится к системе линейных уравнений

, ,(18)

где ,,,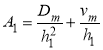

.

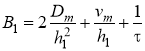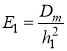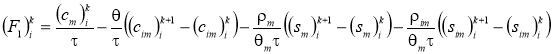Уравнение (4) также после аппроксимации преобразуется к системе линейных уравнений

, , (19)

где, , , ,

.

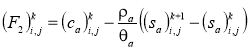Уравнения (12) — (14) после аппроксимации принимают вид

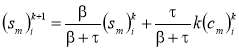,(20)

,(21)

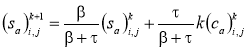.(22)

Схема расчета следующая. Сначала из (20)-(22) определяются значения , , . Решаем систему уравнений (19) методом прогонки определяются . После этого определяем из (2) путем численного интегрирования. Затем решается уравнение (18) для определения .

Далее уравнение (1) решается совместно с уравнением

.(23)

Уравнение (23) после аппроксимации примет вид

,(24)

где .

На основе результатов некоторых численных расчетов определены: поле местной концентрации , профили изменения концентраций , . В случае, когда использовано неравновесное кинетическое уравнение в точке количество адсорбированного вещества до некоторого значения времени увеличивается.

Если коэффициент c, тогда значение в точке через 2700 с. будет равным приблизительно м³/м³. При c значение приблизительно доходило до м³/м³ при c. Таким образом, уменьшение значения приводит к ускорению процесса формирования равновесного режима адсорбции.

На рис.2. представлены результаты обеих подходов. Здесь как и для равновесной адсорбции значение равно 3·10^–6 c^-1. При больших значениях времени ( с) эти результаты отличается.

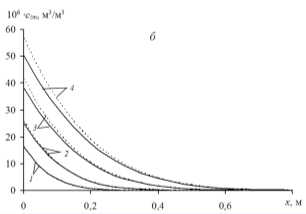
Рис. 2. Профили относительных концентраций (а) и (б) в различные моменты времени при м/с, м²/с, м²/с, , с. для диффузионного подхода (сплошные линии) и кинетического подхода (штриховые линии), 1  c, 2  c, 3  c, 4  c.

Литература:

1. Cussler E. L. Diffusion mass transfer in fluid systems. Cambridge University Press. 1997.
2. Massel R. Principles of Adsorption and Reaction on Solid Surfaces. Jhon Willey and Sons, Inc., NY, 1996. — 804 pp.
3. Oddson, J. K., J. Letey and L. V. Weeks, Predicted distribution of organic chemicals in solution and adsorbed as a function of position and time for various chemical and soil properties // Soil Sci. Soc. Amer. Proc. 1970. 34:412–417.
4. Хужаёров Б. Х., Махмудов Ж. М., Зикиряев Ш. Х. Перенос загрязняющих веществ в водоносных пластах с учетом двухместной адсорбции // Сибирский журнал индустриальной математики. 2011. Т. XIV, № 1(45). С.127–139.
5. Van Genuchten, M.Th. & Wierenga, P.J. 1976, Mass transfer studies in sorbing porous media. 1. Analytical solutions, Soil Sci. Soc. Am. J., 40(4), 473–480.
6. Van Genuchten M.Th., Tang D. H. and Guennelon R., Some exact solutions for solute transport through soils containing large cylindrical macropores // Water Recourses Research. 1984. Vol. 20, № 3. Pp. 335–346.
7. Самарский А. А. Теория разностных схем. — М.: Наука, 1977. — 656 с.