Во многих университетах студенты изучают важную дисциплину «Теория принятия решений», которая использует методы математики, экономики, статистики и психологии с целью изучения закономерностей выбора людьми путей решения проблем и задач, а также способов достижения желаемого результата.
Одним из методов, которые изучают студенты, является двойственный симплекс-метод. Для того чтобы, помочь студентам быстро освоить данный метод была разработана обучающая программа, включающая теорию по данному методу, интерактивное решение задач и проверочный тест, включающая вопросы по теории и практике.
Несмотря на вычислительные ресурсы, которые доступны в современном мире, без оптимизированных методов для решения тех или иных задач не обойтись. В частности двойственный симплекс-метод способствует уменьшению количества ограничений, что существенно упрощает решение больших и ресурсоемких задач.
Перед интерактивным решением задач двойственным симплекс-методом необходимо изучить теорию по данному разделу и получить навыки решения задач линейного программирования симплекс-методом.
В двойственном симплекс-методе решение задачи линейного программирования начинается с недопустимого, но лучшего, чем оптимальное решения. Последовательные итерации этого метода приближают решение к области допустимости без нарушения оптимальности промежуточных решений. Когда будет достигнута область допустимых решений, процесс вычислений заканчивается, так как последнее решение будет оптимальным. В двойственном симплекс-методе начальная симплекс-таблица обязательно должна иметь в базисном решении недопустимую (т. е. отрицательную) переменную.
Реализация двойственного симплекс-метода предполагает наличие двух условий:
Двойственное условие допустимости. В качестве исключаемой переменной xr выбирается базисная переменная, имеющая наибольшее по абсолютной величине отрицательное значение.
Двойственное условие оптимальности. Вводимая в базис переменная определяется как переменная, на которой достигается следующий минимум:
где 
— коэффициент целевой функции, 
– коэффициент из симплекс-таблицы, расположенный на пересечении ведущей строки и столбца, соответствующего переменной xi. При наличии нескольких альтернативных переменных выбор делается произвольно. Коэффициент должен быть строго отрицательным.
Реализация программного средства для интерактивного решения задачи двойственным симплекс-методом выполнена на объектно-ориентированном языке программирования Java.
На рисунке 1 представлена постановка задачи и таблица для заполнения начальными значениями.
Рис. 1. Постановка задачи
Далее переходим ко второму шагу (рисунок 2), где необходимо ввести номер исключаемого и включаемого в базис элемента.
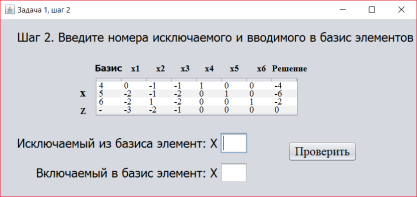
Рис. 2. Второй шаг интерактивного решения задачи
На третьем шаге (рисунок 3) необходимо пересчитать симплекс-таблицу и ввести полученные данные.
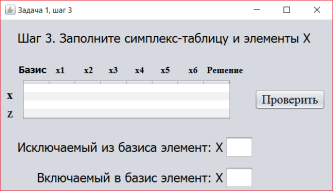
Рис. 3. Третий шаг интерактивного решения задачи
Таким образом производится пересчет симплекс-таблицы пока не будет получено допустимое и оптимальное решение.
Всего для интерактивного решения представлено две задачи на нахождения минимума целевой функции и одна задача на нахождение максимума. Также программное обеспечение предоставляет возможность ознакомиться с теорией по двойственному симплекс-методу и решить тест из десяти вопросов для проверки полученных знаний.
Литература:
- Таха Х. А. Введение в исследование операций 6-е издание. Пер. с англ. — Москва: Издательский дом «Вильямс», 2005. — 912 с.
- Зайченко Ю. П. Исследование операций: Учеб. пособие для студентов вузов. — 2-е изд., перераб. и доп.— Киев: Вища школа. Головное изд-во, 1979. 392 с.
- Герберт Шилдт. Java 8. Полное руководство. — 9-е изд. — Вильямс, 2017. — 1376 с.
