Обоснование эффективности технических решений с использованием парожидкостных термосифонов требует проведения самосогласованных теплотехнических расчетов системы “атмосфера – термосифон – вода” с учетом физико-химических процессов, протекающих в воде [3].
Используемые в настоящее время в расчетах модели тепломассопереноса внутри термосифона основаны на полуэмпирических оценках параметров тепло и массообмена хладагента при заданных граничных условиях [4]. Указанный подход позволяет находить связь между отдельными теплофизическими параметрами термосифона и заданными внешними условиями, но при этом не учитывает комплексное взаимное влияние теплофизических показателей термосифона, атмосферы, воды.
Рассмотрим процессы тепломассопереноса в вертикально расположенном термосифоне. Цилиндрическую систему координат расположим так, чтобы ее центр находился на оси термосифона (рисунок 1).
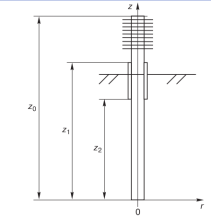
Рис. 1 - Парожидкостной вертикальный термосифон.
В качестве первого приближения рассмотрим изоэнтропное течение пара в трубе термосифона над хладагентом. В этом случае энтропия вдоль линий тока сохраняется [2]. Следовательно, можно записать уравнение Бернулли в виде:
(1)
где 
– удельная теплоемкость пара при постоянном давлении; T – температура; V – скорость пара; g – ускорение свободного падения; z – продольная цилиндрическая координата.
Пусть ρ – плотность пара, Vr , Vz – радиальная и продольная компоненты скорости пара, тогда можно ввести потоки массы 
и 
, которые задаются выражениями:
=
,
(2)
и удовлетворяют уравнению непрерывности:
=0 (3)
Здесь r – радиальная цилиндрическая координата, и – радиальный и продольный поток массы, z – продольная цилиндрическая координата. Кроме того, на границе пара и пленки жидкого хладагента должно выполняться условие:
(4)
где 
– удельный поток тепла, перпендикулярный к границе; e – скрытая теплота парообразования (конденсации).
Вычислим скорость пара на входе в конденсатор. Поскольку весь пар, конденсируясь, отдает в единицу времени тепло Q, можно записать выражение:
(5)
где a – внутренний радиус трубы термоcифона.
Расчет 
по формуле (5) для аммиака, фреона и двуокиси углерода в зависимости от температуры пара и мощности, отдаваемой в атмосферу, показывает, что квадрат скорости много меньше, чем ускорение свободного падения, умноженное на длину термосифона (порядка 10–15 м). Поэтому выражение (1) можно записать в виде:
Следовательно:
где ΔT – перепад температур в термосифоне на расстоянии 
. Поскольку в системе СИ 
порядка 
, а gΔz порядка 
, то для испарителя, длина которого не превышает 10 м, перепад температур ΔT в изоэнтропной модели составляет порядка десятой доли градуса, и, следовательно, температуру хладагента можно считать постоянной по всему объему термосифона. При этом плотность ρ и давление пара p равны плотности и давлению насыщенного пара и зависят от температуры хладоносителя.
Решение уравнения (5) с учетом (6) может быть выражено через тепловой поток на внутренней стороне трубки термосифона (a, z):
(8)
где 
– координата верхней части оребренной поверхности.
Рассмотрим движение пленки по внутренней стенке термосифона. Средняя скорость пленки 
, как следует из работы [6], задается выражением:
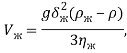(9)
где
, 
– плотность и динамическая вязкость жидкого хладагента соответственно; 
– средняя толщина пленки жидкого хладагента под оребренной поверхностью. Из соотношения (9) легко найти суммарный поток жидкого хладагента 
:
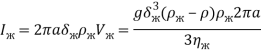(10)
В стационарном случае, очевидно, должно выполняться условие:
(11)
так как
в рамках данной модели от r не зависит. Следовательно:
(12)
Сравнивая (8) и (10), получаем:
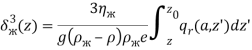(13)
Локальный тепловой поток на внутренней стороне трубки на оребренной поверхности qr(a, z) с учетом термического сопротивления стенки трубы, оребрения и жидкой пленки записывается в виде:
(14)
где 
– коэффициент теплопроводности жидкого хладагента; 
– температура атмосферы; 
–температура хладагента. Величина С задается
следующим выражением:
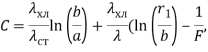(15)
где λ – коэффициент теплопроводности металла, из которого изготовлены ребра; 
– коэффициент теплопроводности металла, из которого изготовлена трубка термосифона; b – внешний радиус трубы термосифона; F – функция геометрических параметров оребренной поверхности.
Продифференцировав обе части выражения (13) по z, с учетом (14) получаем:
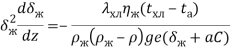(16)
Решение данного дифференциального уравнения записывается в виде:
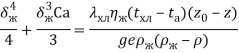(17)
Уравнение (17) имеет единственный положительный корень:
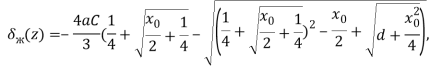(18)
где безразмерные параметры d и 
задаются выражениями:
d=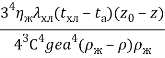
, (19)
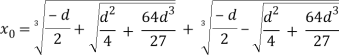
Если ниже оребренной поверхности имеется небольшой участок теплоизолированной трубы, то изменением толщины пленки на его протяжении можно пренебречь, поскольку тепловой поток здесь мал. Следовательно, толщина пленки на выходе из конденсатора (
) находится из выражения (19) подстановкой z = – 
, где – длина оребренной части термосифона:
(z) (20)
Если в выражении (18) полагать C = 0, то получим хорошо известную формулу [6]:
(z)=
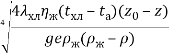(21)
Так как при C = 0 величины термического сопротивления стенки и оребрения равны нулю, то температура стенки равна температуре атмосферы. Однако при расчете теплофизических параметров парожидкостных термосифонов использовать выражение (21) нельзя, поскольку второй член в левой части уравнения (18), как правило, значительно больше первого.
Из уравнения (13) следует, что тепловой поток Q от конденсатора записывается в виде:
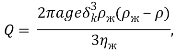(22)
а параметр теплопередачи от одного погонного метра оребренной поверхности 
дается выражением:
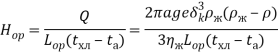(23)
Рассчитаем теперь процессы, происходящие в испарителе. Толщина пленки в испарителе может быть выражена через тепловой поток на внешней
стенке испарителя. Используя соотношение (13) и учитывая, что тепловым потоком от теплоизолированной части термосифона можно пренебречь, для координаты z в испарителе получаем:
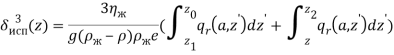(24)
Здесь 
, 
– координаты верхней и нижней границ теплоизолированной части термосифона соответственно. Поскольку выполняются соотношения:
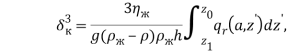(25)
то толщина пленки в испарительной зоне (
) может быть выражена через тепловой поток на границе стенки испарителя и грунта (b, z):
(26)
Здесь толщина пленки выражена через модуль теплового потока, поскольку тепловой поток в испарителе в рассматриваемой системе координат отрицателен. Прямые вычисления показывают, что перепад температур между водой на внешней поверхности испарителя и хладагентом составляет сотые доли градуса, поэтому можно записать:
(27)
Полный тепловой поток, отдаваемый атмосфере, равен:
(28)
Кроме того, в испаритель входит поток 
:
(29)
где 
– коэффициент теплопроводности воды.
Из выражения (28) следует, что:
(30)
Здесь 
– площадь испарителя; 
– среднее значение температуры на границе воды и испарителя, равное:
(31)
(
– длина испарителя). Из теплового баланса вытекает, что суммарный поток, проходящий через термосифон, равен нулю. Следовательно:
(32)
где 
– эффективный коэффициент теплопередачи от воды к атмосфере, который находится из выражения = 
/ .
Далее, рассмотрим процессы, происходящие в воде. Будем считать, что равновесная температура замерзания воды равна 0 °C. Термическое сопротивление участка от воды до парообразного хладагента 
определяется выражением [1]:
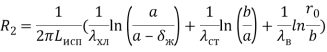(33)
где 
– радиус промерзания воды, заданный нулевой изотермой.
Термическое сопротивление термосифона от внешней границы испарителя до парообразного хладагента 
дается выражением:
(34)
Если принять
= 0,5⋅
м, = 0,556 Вт/(м⋅°С), 
= 57 Вт/(м⋅°С), = 0,54 Вт/(м⋅°С) для аммиака, = 0,13 Вт/(м⋅°С) для двуокиси углерода , , = 0,086 Вт/(м⋅°С) для фреона (R12), a = 0,013 м, b = 0,01685 м,= 0,1 м, то получим:
для аммиака:
(35)
Для двуокиси углерода:
(36)
Для фреона:
(37)
Как следует из (35), (36), (37), в испарителе, в отличие от конденсатора, процессы тепломассопереноса от внешней границы испарителя к парообразному хладагенту на работу термосифона практически не влияют, и она полностью определяется процессами, происходящими в воде. Мощность, отдаваемая испарителю водой, в рамках двумерной задачи записывается следующим образом:
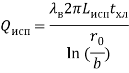(38)
Поскольку выполняется условие теплового баланса Q + = 0, из (28) и (37) получаем:
(39)
Следовательно:
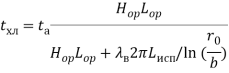(40)
Учитывая, что Q = – , и подставляя (38) в (37), получаем:
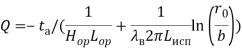(41)
Таким образом выражение (41) характеризует процесс интенсивности образования льда вокруг термосифона. Анализируя данное выражение установлено, что значительное влияние на рассматриваемый процесс оказывают следующие факторы: 
, 
, .
Однако, помимо рассматриваемых факторов, важную роль на холодопроизводительность термосифона играет такой параметр, как скорость ветра. Влияние этого фактора в рассматриваемом процессе учитывается при расчетах коэффициентом 
, полученным аналитическим методом. Следовательно, процесс образования льда характеризуется выражением [5]:
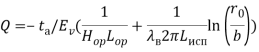(42)
Величина вычислена по формуле (27), при этом коэффициент теплоотдачи от металлической поверхности к воздуху, входящий в рассчитывался:
(43)
где – коэффициент теплопроводности для воздуха;
– число Прандтля; Re – число Рейнольдса; s – расстояние между ребрами; 
– толщина ребра у его основания и окончания соответственно; l – длина межреберного интервала; 
– внутренний радиус ребра; 
– внешний радиус ребра.
Расчеты показывают сильную зависимость тепловой мощности термосифона и температуры хладагента от радиуса промерзания. В то же время от типа хладагента зависимость слабая.
Таким образом, в работе представлена изоэнтропная модель тепломассопереноса в вертикальном парожидкостном термосифоне, основанная на решении уравнений газовой и гидродинамики.
Литература:
- Аникин Г.В. Тепломассо-перенос в вертикальном парожидкостном термосифоне [Текст] / Аникин Г.В., Поденко Л.С., Феклистов В.Н.// Тюмень.: Криосфера Земли т. 8 №3. 2008. – с. 54-58.
- Вукалович М.П. Термодинамика. Учебное пособие для вузов [Текст]/ М.П. Вукалович, И.И. Новиков// М., Машиностроение, 1972, 672 с.
- Коровин Г.С. Энергосберегающий метод охлаждения молочной продукции [Текст]/ Г.С. Коровин, В.И. Квашенников, А.П. Козловцев// Известия ОГАУ. – 2013. – № 3. – С. 97 – 99.
- Коровин Г.С. Терминология при производстве и эксплуатации ледогенераторов [Текст]/ Г.С. Коровин В.И. Квашенников, А.П. Козловцев, В.А. Шахов// Механизация и электрификация сельского хозяйства. – 2014. - № 2. – С. 30 – 32.
- Коровин Г.С. Энергосберегающая технология заготовки естественного льда на молочных фермах [Текст]/ Г.С. Коровин В.И. Квашенников, А.П. Козловцев, В.А. Шахов // Научное обозрение. – 2015. - № 4. – С. 17 – 22.
- Кутателадзе С.С. Основы теории теплообмена [Текст]/ Кутателадзе С.С.// М., Атомиздат. – 1979. – 416с.
