Вопрос о геометрических размерах частиц, движущихся в сплошной среде со столкновениями равностепенным шагом по времени, достаточно сложны для гамильтоновой динамики в окружающем фазовом пространстве. В случае слабо-диссипативной динамики мы имеем возможность по-разному оценивать размеры движущихся частиц. В частности, оценка диффузии молекул в теории колебаний пробных частиц в окружающей среде прекрасно возможно с помощью слабо-диссипативных моделей. Появление времени наблюдения приводит к определенным вопросам.
Формулы Ланжевена имеют диффузионный характер и прямопропорциональны времени наблюдения. Они пригодны для оценки ответа при согласовании времен наблюдения. У нас время наблюдения ![]() (при условии, что шаг по времени около единицы). Ланжевеновские формулы позволяют рассчитывать размеры движущихся частиц в сплошной среде. По словам Пуанкаре, в математической физике расчёт должен сопровождаться двумя критериями. Первое замечание к критериям заключается в необходимости вместо главного приближения использовать даже асимптотические ряды с актуальным вопросом их обрыва. Второе замечание к критериям заключается в необходимости использования другой методики того же самого результирующего расчета. Критерий в данном случае расчётов даёт нам новую методику оценки размеров частиц.
(при условии, что шаг по времени около единицы). Ланжевеновские формулы позволяют рассчитывать размеры движущихся частиц в сплошной среде. По словам Пуанкаре, в математической физике расчёт должен сопровождаться двумя критериями. Первое замечание к критериям заключается в необходимости вместо главного приближения использовать даже асимптотические ряды с актуальным вопросом их обрыва. Второе замечание к критериям заключается в необходимости использования другой методики того же самого результирующего расчета. Критерий в данном случае расчётов даёт нам новую методику оценки размеров частиц.
Периодические траектории бывают асимптотически устойчивыми или неустойчивыми в зависимости от характера движения. И в том, и в другом случае они характеризуются областью захвата или отталкивания. Эти площади, переведённые в линейные размеры и дают нам вторую оценку движущихся частиц, которую можно сравнивать с ланжевеновскими формулами. У ланжевеновских формул есть один недостаток — время наблюдения, которое фигурирует ниже. При очень большом времени наблюдения эти формулы строятся безусловно недостаточными для расчёта. Поэтому сравнение этих двух методик позволяет принять решение о рабочем интервале наших движений.
Распределение пробных частиц по размерам при кусочно-свободном движении выглядит весьма странным вопросом (ср. Ван-дер Поль, Клаузиус, П. Л. Капица, Н. Н. Боголюбов, А. Н. Колмогоров, В. И. Арнольд, Д. В. Аносов, В. А. Садовничий.). Ответ — в простейшем случае движения частицы в течение постоянного цикла по времени в поле гармонического осциллятора слабо-возмущенного силами вязкости. Нормализованная форма движения дается в виде
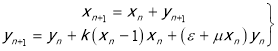 ,
,
где ![]() — малые параметры (см. [1,2]). Мы исходим из формулы Ланжевена
— малые параметры (см. [1,2]). Мы исходим из формулы Ланжевена ![]() , где
, где ![]() — дисперсия фазовой координаты, R — универсальная газовая постоянная, T — температура, N — число Авогадро,
— дисперсия фазовой координаты, R — универсальная газовая постоянная, T — температура, N — число Авогадро, ![]() — коэффициент вязкости,
— коэффициент вязкости, ![]() — размер частицы,
— размер частицы, ![]() — время наблюдения частицы. Обращая равенство относительно
— время наблюдения частицы. Обращая равенство относительно ![]() , мы получаем распределение по найденным периодическим орбитам геометрических размеров пробных частиц в слабо-диссипативной теории КАМ. На рисунке показана зависимость геометрических размеров пробной частицы от частоты колебаний при
, мы получаем распределение по найденным периодическим орбитам геометрических размеров пробных частиц в слабо-диссипативной теории КАМ. На рисунке показана зависимость геометрических размеров пробной частицы от частоты колебаний при ![]() ~10-5.
~10-5.
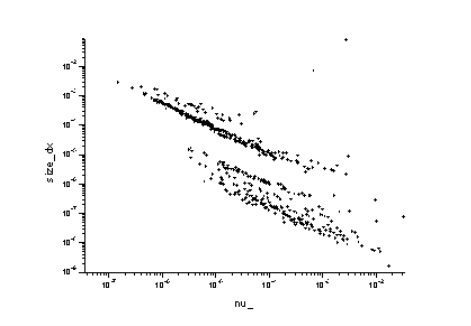
Рис. 1. Наблюдение за размерами частиц с учётом дисперсии координаты
Нужно заметить, что периодические асимптотически (не)устойчивые движения образуют дискретный набор движений в нашей модели. Таким образом, мы имеем не распределение характеристик, а точечные наборы. Эти точечные наборы относятся к асимптотически (не)устойчивым движениям нашей модели. Таким образом, раньше мы показывали периоды асимптотически квазиоднородных движений, частоты этих движений и т. д. Теперь мы в состоянии для периодических движений оценить размеры движущихся частиц в сплошной среде. Мы приводим температуру для наших движений, которые мы наблюдаем в сплошной среде.
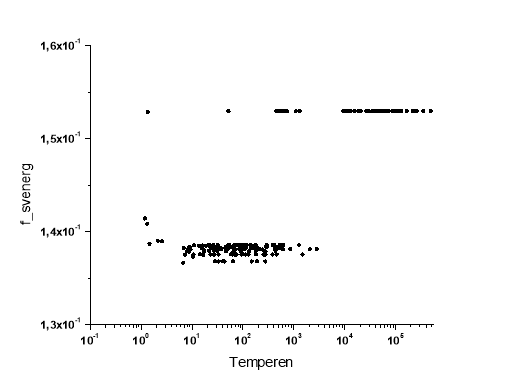
Рис. 2. Зависимость свободной энергии от температуры для асимптотически устойчивых орбит
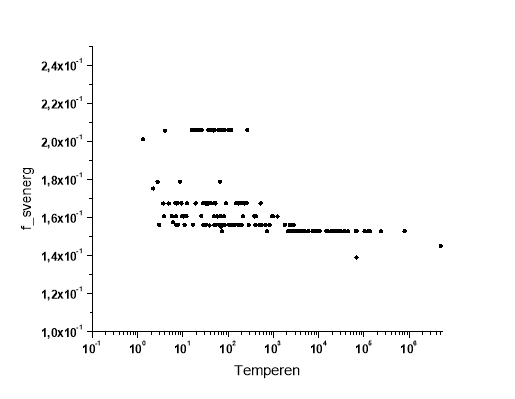
Рис. 3. Зависимость свободной энергии от температуры для асимптотически неустойчивых орбит
Мы должны сказать, что все цифры, которые приведены выше, получены компьютерными вычислениями. Наша дискретная модель, которой мы пользуемся, имеет довольно-таки простую асимптотику наших физических приближений. При этом мы наконец-то сумели посчитать размеры движущихся частиц и показать такие важные характеристики, как температура и давление движущихся частиц. Поэтому интерес вызывает, что же будет происходить с нашей расчётной моделью, если мы будем менять расчётные формулы для исходного движения. В частности, для нас важно, всегда ли кривые, будут монотонными. Мы видим, что наши кривые — монотонные. Как они меняют свою монотонность, нам нужно устанавливать дополнительными расчётами.
Литература:
- Ланжевен П. Избранные труды. — М.: Изд-во АН СССР, 1960г., 755 с.
- Ландау Л. Д., Лифшиц Е. М. Квантовая механика (нерелятивистская теория). — Издание 6-е, исправленное. — М.: Физматлит, 2004. — 800с. — («Теоретическая физика», том III).
- Боголюбов Н. Н. Собрание научных трудов: в 12т. T.S.: Механика, 1939–1980/ ред. И. И. Плакида, А. Д. Суханов — 2006, 804 с.
- Колмогоров А. Н. Юбилейное издание в 3-х книгах. Книга 1. Истина — благо. Библиография/ Ред.-совет Ширяев. — М: ФИЗМАТ ЛИТ, 2003, – 384с.
- Богданов Р. И. Нелинейные динамические системы на плоскости и их приложения. — М.: Вузовская книга, 2003. 376 с.
- Арнольд В. И. Особенности каустик и волновых фронтов (Библиотека математика. Вып. 1). М.: ФАЗИС, 1996.
- Планк М. Избранные труды. Термодинамика. Теория излучения и квантовая теория. Теория относительности. Статьи и речи. – М.: «Наука», 1975, 788 с.
- Блохинцев Д. И. Избранные труды в 2 т. Т. 2. – М.: Физматлит, 2009, 744 с.
- Нейман Дж. Математические основы квантовой механики. М.: Наука, 1964.
- Арнольд В. И. Волновые фронты и топология кривых. — М: ФАЗИС 2002 г, 118 с.
- Арнольд В. И. Лекции об уравнениях с частными производными. — М: ФАЗИС 1999 г, 180 с.
- Arrowsmith D. K., Cartwright J. H. E., Lansbury A. N., Place C. M. The Bogdanov-map: bifurcations, mode locking, and chaos in a dissipative system // International Journal of Bifurcation and Chaos, 1993, v. 3. № 4, p. 803–842.
- Belotserkovsrii O. V. Turbulence and Instabilities /. M: MZpress, 2003, 460 p.
- R. I. Bogdanov, S. N. Nagornykh and M. R. Bogdanov. New Nature of the Noise of Thermally Stimulated Electron Emission from Rods under Cyclic Torsion.: Journal of Surface Investigation, X-ray, Synchrotron and Neutron Techniques, 2007, с. 157–166.
- Андронов А. А., Леонтович В. А., Гордон И. И., Майер А. Г. Качественная теория динамических систем. М., 1966.
- Арнольд В. И. Лекции о бифуркациях и версальных семействах. // УМН, т. 27, № 5, 1972, с. 119–184.
- Андронов А. А., Леонтович Е. А., Гордон И. И., Майер А. Г. Теория бифуркаций динамических систем на плоскости. М.: Наука, 1967.
- Андронов А. А., Хайкин С. Э., Витт А. А. Теория колебаний. М.: Физматгиз,1959.
- Богданов Р. И. Богданов М. Р. Турбулентность в рамках слабо-диссипативной версии теории КАМ. Тезисы докладов международной конференции «Анализ и особенности», посвященная семидесятилетию Владимира Игоревича Арнольда 20–24 августа Москва 2007, с. 35–38.
- Богданов Р. И. Фазовые портреты динамических систем на плоскости и их инварианты. — М.: Вузовская книга, 2008, 428 с.
- Богданов Р. И., Богданов М. Р. Свойства странного аттрактора в слабо-диссипативной теории Колмогорова-Арнольда-Мозера. Труды международной конференции «DIFF2008», 27 июня — 1 июля 2008. Суздаль — Владимир, Владимирский государственный университет, с. 54–55.
- Богданов Р. И., Богданов М. Р. Статистики в слабо-диссипативной теории Колмогорова-Арнольда-Мозера. Тезисы докладов международной конференции «Дифференциальные уравнения и топология», посвященная 100-летию со дня рождения А. С. Понтрягина, Москва, 17–22 июня 2008. – М: Издательский отдел факультета ВМК МГУ им. М. В. Ломоносова, МАКС Пресс, 2008, с. 100–101.
- Богданов Р. И., Богданов М. Р. Тепловые характеристики струйных течений в слабо-диссипативной теории Колмогорова-Арнольда-Мозера. // ДАН. 2008, т. 423, № 5, с. 1–4.
- Богданов Р. И., Богданов М. Р. Переход от развитой турбулентности к квазиравновесному состоянию. // Научный Вестник МГУ ГА, серия Математика и физика. № 114, 2007, с. 50–55.
- Богданов Р. И., Богданов М. Р. Слабо-диссипативная версия теории Колмогорова-Арнольда-Мозера: теория и практика расчетов. // Ж. вычисл. матем. и матем. физ. 2008, т. 48, № 3, с. 73–90.
- Богданов Р. И., Богданов М. Р. Структурообразование в слабо-диссипативной теории Колмогорова-Арнольда-Мозера. // ДАН. 2008, т. 418, № 6, с. 754–758.
- Богданов Р. И., Богданов М. Р. Новый механизм микроразрушений твердого тела. В книге «Упругость и неупругость», Материалы Международного научного симпозиума по проблемам механики деформируемых тел, посвященный 95-летию со дня рождения А. А. Ильюшина, под редакцией И. А. Кийко, Р. А. Васин, Г. Л. Бровко, М.: ЛЕНАНД, 2006, с. 295–300.
- Bogdanov R. I., Bogdanov M. R. Estimation of the Density Particle Fluxes in the Weakly Dissipative Kolmogorov-Arnol’d-Mozer theory. Journal of Surface Investigations. X-ray, Synchrotron and Neutron Techniques, 2010, Vol. 4, № 2, pp. 269–275.
- Богданов Р. И., Богданов М. Р., Термодинамические симметрии в слабо-диссипативной теории КАМ. Научный вестник МГТУ ГА, серия Математика и физика, № 156, 2011, с. 5–12.
- Богданов Р. И., Богданов М. Р., Кузин П. С. Непрерывные бильярды и слабо-диссипативная КАМ-теория. Проблемы математического анализа, в. 67, ноябрь 2012, с. 9–12 (см. англ. Bogdanov R. I., Bogdanov M. R., Kuzin P. S. Continuous Billiards and the Weakly Dissipative Kolmogorov-Arnold-Moser Theory. Journal of Mathematical Sciences, vol. 188, № 3, January, 2013, pp. 181–184).
- Богданов Р. И., Богданов М. Р., Кузин П. С. Фрактальные структуры в слабо-диссипативной теории КАМ и смежные проблемы. Современная математика и её приложения, том 78 (2012), с. 3–10 (см. англ. Bogdanov R. I., Bogdanov M. R., Kuzin P. S. Fractal Structures in weakly dissipative KAM-theory. // Journal of Mathematical Sciences, vol. 189, № 2, February, 2013, pp. 173–180).
- Богданов Р. И., Богданов М. Р. Методы вычислений и шкалы функциональных пространств. Современная математика и её приложения, том 78 (2012), с. 10–16 (см. англ. Bogdanov R. I., Bogdanov M. R., Methods of Evaluation and scale of functional spaces. Journal of Mathematical Sciences, vol. 189, № 2, February, 2013, pp. 181–187).
- Богданов Р. И., Богданов М. Р., Кузин П. С. Теория прямых измерений, теория Ито-Стратоновича и слабо-диссипативная теория Колмогорова-Арнольда-Мозера. Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2012, № 3, с. 99–106 (см. англ. Bogdanov R. I., Bogdanov M. R., Kuzin P. S. Direct Measurement Theory, Ito–Stratonovich Theory, and Weakly Dissipative Kolmogorov–Arnold–Moser Theory. Journal of Surface Investigation. X-ray, Synchrotron and Neutron Techniques, vol. 6, 2012, p. 280–286).
- Богданов Р. И., Богданов М. Р. От Ньютона к слабо-диссипативной версии КАМ-теории. Современная математика и её приложения, т. 76, Геометрия и механика, 2012, с. 12–19 (см. англ. Bogdanov R. I., Bogdanov M. R. From the Newton version of the Kolmogorov-Arnold-Moser theory to a weakly dissipative version. Journal of Mathematical Science vol. 187, № 3, December, 2012, pp. 272–279).
- Больцман Л. Избранные труды. Молекулярно-кинетическая теория газов. Термодинамика. Статистическая механика. Теория излучения. Общие вопросы физики. — М.: «Наука», 1984, 590 с.
- Бор Н. Избранные научные труды. В двух томах. Т. 1, 1970, 583 с., Т. 2, 1971, 675 с., — М.: «Наука».
- Заславский Г. М. Гамильтонов хаос и фрактальная динамика. — М.-Ижевск: НИЦ «Регулярная и хаотическая динамика», Ижевский институт компьютерных исследований, 2010, 472 с.
- Зоммерфельд А. Термодинамика и статистическая физика. М: Изд-во иностр. лит-ры, 1955, 479с.
- Мищенко Е. Ф., Садовничий В. А., Розов Н. Х., Колесов А. Ю. Автоволновые процессы в нелинейных средах с диффузией. М.: Физматгиз, 2010.
- Нейман Дж. Математические основы квантовой механики. М.: Наука, 1964.
- Планк М. Избранные труды. Термодинамика. Теория излучения и квантовая теория. Теория относительности. Статьи и речи. – М.: «Наука», 1975, 788с.
- Пуанкаре А. О кривых, определяемых дифференциальными уравнениями. М.; Л.: Гостехисздат, 1947.
- Фриш У. Турбулентность. Наследие А. Н. Колмогорова. Перевод с англ. А. Н. Соболевского под редакцией М. Л. Бланка. — М.: ФАЗИС, 1998, XIV — 346 с.







