Библиографическое описание:
Булгакова, З. Р. Устойчивость железобетонного изгибаемого элемента (балки) под действием равномерно распределенного изгибающего момента / З. Р. Булгакова. — Текст : непосредственный // Молодой ученый. — 2017. — № 19 (153). — С. 40-43. — URL: https://moluch.ru/archive/153/43282/ (дата обращения: 19.04.2024).
В статье анализируются задача на устойчивость железобетонного изгибаемого элемента под действием равномерно распределенного изгибающего момента, решенная ПК «ANSYS».
Определяются формы потери устойчивости и значение критического изгибающего момента. Итоговые значения сравниваются со значениями теоретических результатов по книге А. В. Перельмутера, В. И. Сливкера «Устойчивость равновесия конструкций и родственные проблемы» на стр. 582.
Ключевые слова: устойчивость, железобетонная балка, изгибаемый элемент, изгибающий момент, критические нагрузки
Железобетонная балка задана в виде двух КЭ-моделей:
1.В стрежневой, где изгибающий момент задан сосредоточенными моментами, приложенными на узлы.
2.В объемной, где рассматривалось два варианта закрепления балки: по нижней грани и на уровне половины высоты торца балки, а изгибающий момент задавался как пара сил, равномерно распределенных по верхней и нижней граням.
Момент задавался со значением mизг= 1 т∙м/м.
Определения критических моментов и форм потери устойчивости решались методом Ланцоша. Задавались 10 шагов нахождения критических моментов и соответствующих им потери устойчивости.
Таблица 1
Сопоставление результатов расчёта
|
|
|
Критический погонный изгибающий момент, mизг,
|
|
№задачи
|
№формы
|
|
ANSYS
|
т∙м/м
|
Теория
|
δ(%)
|
|
|
|
Стержневая
|
Объмная
|
Объмная
|
[1]
|
|
|
|
|
КЭ-модель
|
КЭ-модель
|
КЭ-модель*
|
|
|
|
1
|
1
|
756,727
|
723,615
|
657,227
|
755,567
|
0,154
|
|
|
2
|
1322,000
|
1350,000
|
1344,000
|
-
|
|
|
|
|
|
|
|
|
|
*- закрепление по нижней грани балки.
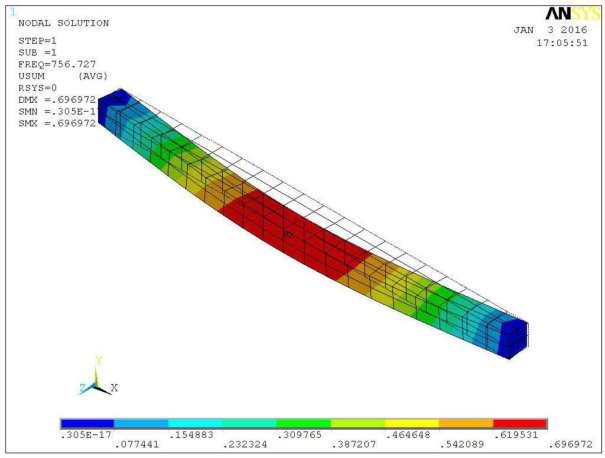
Рис. 1. 1-я форма потери устойчивости для объемной КЭ-модели (закреплена по нижней грани). mизг = 756,727 т·м/м
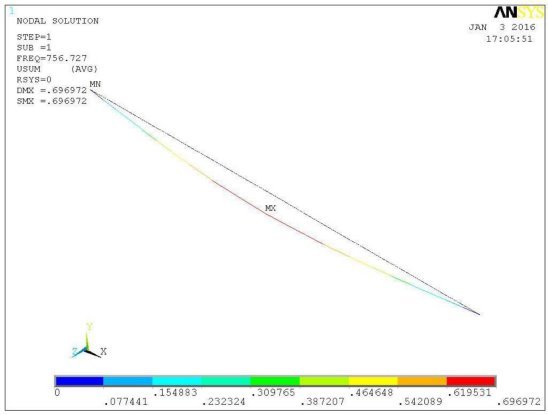
Рис. 2. 1-я форма потери устойчивости для стержневой КЭ-модели. mизг =756,727 т·м/м
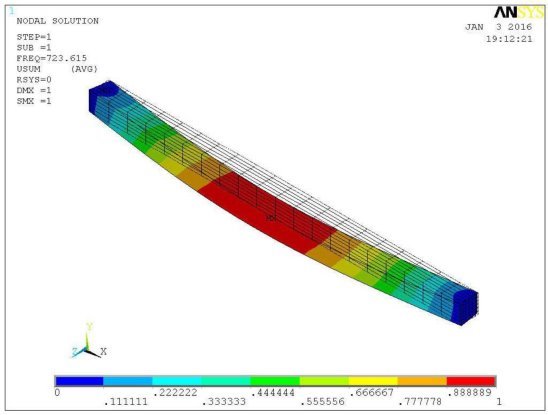
Рис. 3. 1-я форма потери устойчивости для объемной КЭ-модели (закреплена на уровне половины высоты торца). mизг = 723,615т·м/м

Рис. 4. 2-я форма потери устойчивости для объемной КЭ-модели (закреплена по нижней грани). mизг = 1322,000т·м/м
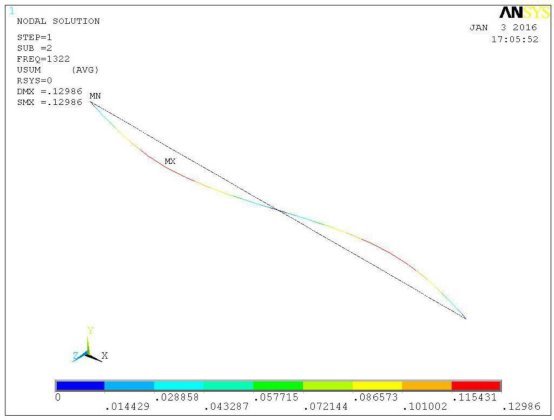
Рис. 5. 2-я форма потери устойчивости для стержневой КЭ-модели. mизг =1322,000т ·м/м

Рис. 6. 2-я форма потери устойчивости для объемной КЭ-модели (закреплена на уровне половины высоты торца). mизг = 1344,000·м/м
Литература:
-
Перельмутер А. В., Сливкер В. И. Устойчивость равновесия конструкций и родственные проблемы — М.,“СКАД СОФТ”, 2007 — С. 551–554
-
Баженов Ю. М. Технология бетона. — М.: Высшая школа, 1978.
-
Ахметзянов Ф. Х. К особенностям деформирования, повреждаемости, изменения физико-механических характеристик бетона в конструкциях // Известия вузов. Строительство, 1993, № 9. — С. 150–155.
-
Попов Л. Е., Пудан Л. Я., Колупаева С. Л., Кобытев В. С., Старенченко В. А. Математическое моделирование пластической деформации. — Томск, ТГУ, 1990. — С. 325.
Основные термины (генерируются автоматически): объемная КЭ-модель, изгибающий момент, ANSYS, железобетонная балка, стержневая КЭ-модель, уровень половины высоты торца, форма потери устойчивости.
Похожие статьи
где Mx — изгибающий момент относительно оси x
усиление, усиливающий элемент, железобетонный элемент, деформационная модель, поперечное сечение, деформации, элементарный участок.
Усиления железобетонных балок перекрытия углепластиком.
Ключевые слова: железобетон, нелинейная деформационная модель, наращивание сечения, железобетонный элемент, усиление, диаграммный метод.
Эти выражения справедливы для не усиленных элементов, на которые действует изгибающие моменты в двух взаимно...
Устанавливаем соответствие между параметрами конечного элемента стандартного вида и параметрами всей расчетной модели.
Устойчивость железобетонного изгибаемого элемента (балки) под действием равномерно распределенного изгибающего момента.
Для расчета несущих конструктивных систем согласно [1] рекомендуется использовать расчетные модели
Распределение изгибающих моментов, полученных из расчета заменяющей рамы
Совместная работа железобетонных плит перекрытий и стальных балок.
Определяем изгибающие моменты от расчётной и нормативной нагрузок по формулам (2)
Определяем статический момент балки относительно оси Х по формуле (8)
Расширенный порядок расчета усиления железобетонных элементов на основе деформационной модели.
Опытные образцы коротких железобетонных балок имели следующий характер трещинообразования: одновременно с наклонной
В дальнейшем трещина Т–Р практически не развивается, и длина ее к моменту разрушения образца составляет 0,25 общей высоты балки.
Исследование напряженно-деформированного состояния железобетонной балки при наличии трещины.
Построение модели. Для исследования влияния наличия трещины на напряженно-деформированное состояние железобетонной конструкции с помощью ANSYS моделируется...
Потеря устойчивости — одна из наиболее распространенных проблем стержней, работающих на сжатие.
Определим изгибающий момент в некотором сечении.
. Последнее уравнение задает первую из отклоненных форм равновесия стержня [3].
где Mx — изгибающий момент относительно оси x
усиление, усиливающий элемент, железобетонный элемент, деформационная модель, поперечное сечение, деформации, элементарный участок.
Усиления железобетонных балок перекрытия углепластиком.
Ключевые слова: железобетон, нелинейная деформационная модель, наращивание сечения, железобетонный элемент, усиление, диаграммный метод.
Эти выражения справедливы для не усиленных элементов, на которые действует изгибающие моменты в двух взаимно...
Устанавливаем соответствие между параметрами конечного элемента стандартного вида и параметрами всей расчетной модели.
Устойчивость железобетонного изгибаемого элемента (балки) под действием равномерно распределенного изгибающего момента.
Для расчета несущих конструктивных систем согласно [1] рекомендуется использовать расчетные модели
Распределение изгибающих моментов, полученных из расчета заменяющей рамы
Совместная работа железобетонных плит перекрытий и стальных балок.
Определяем изгибающие моменты от расчётной и нормативной нагрузок по формулам (2)
Определяем статический момент балки относительно оси Х по формуле (8)
Расширенный порядок расчета усиления железобетонных элементов на основе деформационной модели.
Опытные образцы коротких железобетонных балок имели следующий характер трещинообразования: одновременно с наклонной
В дальнейшем трещина Т–Р практически не развивается, и длина ее к моменту разрушения образца составляет 0,25 общей высоты балки.
Исследование напряженно-деформированного состояния железобетонной балки при наличии трещины.
Построение модели. Для исследования влияния наличия трещины на напряженно-деформированное состояние железобетонной конструкции с помощью ANSYS моделируется...
Потеря устойчивости — одна из наиболее распространенных проблем стержней, работающих на сжатие.
Определим изгибающий момент в некотором сечении.
. Последнее уравнение задает первую из отклоненных форм равновесия стержня [3].













