В работе рассмотрен новый метод идентификации сигналов, основанный на вводимых авторами псевдосплошных образах. Это позволяет передавать информацию более эффективно, чем при использовании применяемых методов модуляции сигнала. Данный подход значительно облегчает моделирование сложных измерительно-управляющих систем, особенно при наличии большого числа параллельно-функционирующих компонентов.
Наряду с числовой, матричной и векторной математиками, можем рассматривать и образную математику, единицей информации которой является сплошной образ. Сплошным образ становится тогда, когда размеры его пикселей стремятся к нулю. Образная математика удобна для теоретического исследования нервных систем живых существ, а также для измерительно-управляющих систем, действующих по родственным принципам [1,2]. Иными словами, данный раздел математики более всего подходит для работы с системами искусственного интеллекта, нейронными и нейроподобными системами.
Итак, рассмотрим подробнее, что будем понимать под образной математикой. Основной единицей информации в ней выступает не число — или символ, его заменяющий — не матрица чисел и не вектор, а сплошной образ. Сплошной образ — это такой образ, у которого размеры отображающих его элементов стремятся к нулю.
Действия образной математики различаются от числовой математики — вместо сложения, вычитания, умножения, деления, логарифмирования, дифференцирования, интегрирования и прочих операций с числами, должны появиться операции с отдельными образами. К ним мы можем отнести: усиление, ослабление, суммирование образов, насыщение, разбавление, негативизацию, разделение, расширение, сжатие, поднятие и опускание уровней, изменения контрастности, пропорциональное изменение, аккомода-ция, изменение во времени и т. д.
Помимо операций с отдельными образами, необходимо использовать и их совместную обработку, а именно:
– активацию пассивного образа активным;
– просветление одного образа другим, т. е. сложение образов;
– затемнение образов, т. е. вычитание одного из другого;
– определение степени сходства образов и др.
Новыми в случае рассмотрения операций над образами будут не только сами процедуры математических операций, но и аппаратные средства для их реализации. Следует отметить, что прикладные направления образной математики имеют весьма широкие перспективы в различных областях человеческой деятельности, особенно там, где требуется минимум затрат для решения сложных задач, где программное обеспечение невыполнимо вследствие неограниченного роста числа учитываемых видов информации. Особенно важным это становится в сложных системах с параллельно функционирующими компонентами. Чем выше число компонентов и, соответственно, сложность системы, тем важнее становится использование подобных методик [3,4,6].
Особой областью применения прикладной образной математики являются теоретические исследования живых и искусственно разработанных нервных систем (обучаемых систем искусственного интеллекта).
Любой сигнал можно представить как сплошной образ. Если при сравнении этого образа с другими возникает совпадение с одним из уже имеющихся, то сразу получаем всю информацию, закодированную в пришедшем сигнале. Такой подход намного эффективнее, чем различные методы модуляции, используемые на данный момент [6].
В современной технике выполнить условие стремления элемента, отображающего образ, к нулю нереально. Именно поэтому следует говорить о псевдосплошных образах. Псевдосплошной образ — образ, размер пикселя которого имеет конечное значение и ему соответствует некий определенный элемент матрицы псевдосплошного образа. Форму элемента, отображающего псевдосплошной образ, будет определять сетка. Под сеткой будем понимать линии, разбивающие плоскость на конечные ячейки, которые в свою очередь будут являться элементами псевдо-сплошного образа.
Сигнал поступает в нейрон, после чего накладывается на сетку, которая в данном случае является псевдо-сплошным образом. Данный процесс представлен на рисунке 1.
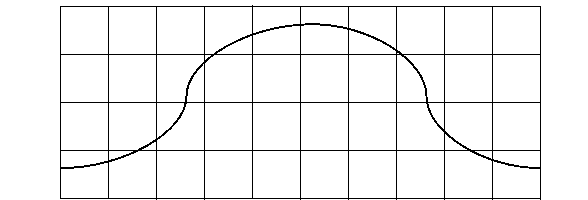
Рис. 1. Наложение сигнала на сетку
После наложения сигнала на сетке как бы отпечатывается псевдо-сплошной образ. Это происходит по следующему алгоритму. При прохождении линии сигнала через пиксель сетки, он просветляется. В случае, когда линия сигнала не проходит через пиксель, он остается в безразличном состоянии. Пример для нашего сигнала представлен на рисунке 2.
Фактически каждый пиксель может представлять собой элемент матрицы. Назовем такую матрицу матрицей псевдосплошного образа. В ней элемент будет равен нулю если:
– находится в безразличном (полностью затененном) состоянии;
– имеет какое-то значение если его просветлил сигнал, пришедший в нейрон.

Рис. 2. Псевдо-сплошной образ, полученный при наложении сигнала на сетку
Такую матрицу можно поэлементно сравнить с матрицей уже сохраненной в памяти. Сравнение происходит наложением соответствующих элементов друг на друга (рис. 3).
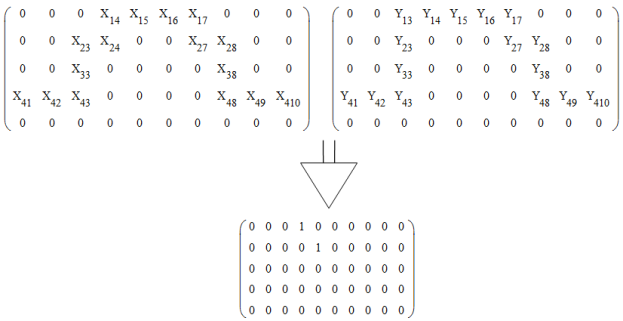
Рис. 3. Наложение матрицы псевдосплошного образа с матрицей сравнения и формирование матрицы соответствия
Результатом проведенного сравнения является матрица, элементами которой являются нули в случаях наложение ненулевого элемента одной на не нулевые элементы другой или нулевые элементы одной на нулевые элементы другой. В единичное значение элемент матрицы устанавливается в случае наложения ненулевого элемента одной матрицы на нулевой элемент другой или при наложении нулевого элемента на нулевой элемент. В случаях, когда не будет найдено не одного совпадения, будет активирована система обучения. В данной статье не приводятся алгоритмы ее работы и собственно общая методика. Однако, в последующих работах это будет рассмотрено в должной степени.
При использовании предложенного метода в распознавании образов получаем два существенных преимущества. Во-первых, идентификация сигналов с помощью псевдосплошных образов позволит передавать информацию в более скомпонованной форме, чем при различных видах модуляции сигнала. Во-вторых, при использовании разрабатываемых авторами нейроподобных систем [7], данный подход приближен к работе биологических нейронов, в которых сигнал восприниматься как какой-то образ, а не модулированный электрический сигнал.
Литература:
- Фу К. Структурные методы в распознавании образов. М.: Мир, 1977. — 345 с.
- Ту Дж, Гонсалес Р.. Принципы распознавания образов. М.: Мир, 1978. — 298 с.
- Поляков В. С. Моделирование параллельно протекающих процессов блоками взаимодействующих компонентов. / В. С. Поляков, С. В. Поляков // Контроль. Диагностика — 2008. — № 8. — С. 70–73.
- Поляков С. В. Построение модели для диагностирования технологических процессов с использованием графов. /С. В. Поляков, С. Б. Сластинин // Контроль. Диагностика — 2000. — № 4. — С. 19–22.
- Зыков А. А. Теория конечных графов / А. А. Зыков. — Новосибирск: Наука, 1968. — 541 с.
- Барский. А. Б. Нейронные сети: распознавание, управление, принятие решений / М.: Финансы и статистика, 2004. — 176 с.
- Поляков В. С. Системы оперативной и долгосрочной памяти при моделировании нейроподобных систем управления. / Н. В. Полежаев, М. Д. Хорошевский // Известия ВолгГТУ. Серия «Прогрессивные технологии в машиностроении». Вып. 9: межвуз. сб. науч. ст. / ВолгГТУ. — Волгоград, 2013. — № 7 (110). — C. 101–105.







