Блочно-операторная матрица — это матрица элементы которой являются линейными операторами в банаховым или гильбертовом пространстве. Пусть ![]() –две гильбертовы пространства и
–две гильбертовы пространства и ![]() . Тогда известно, что всякий линейный ограниченный оператор
. Тогда известно, что всякий линейный ограниченный оператор ![]() , действующий в
, действующий в ![]() всегда представляется как
всегда представляется как ![]() блочно-операторная матрица
блочно-операторная матрица
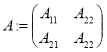 (1)
(1)
с линейными ограниченными операторами ![]() .
.
Пусть ![]() — множество комплексных чисел и
— множество комплексных чисел и ![]() – пространство линейных ограниченных операторов в гильбертовом пространстве
– пространство линейных ограниченных операторов в гильбертовом пространстве ![]() . Следующие операторы
. Следующие операторы
![]()
![]()
называются дополнениями Шура соответствующий блочно-операторной матрицы ![]() и они играют важную роль в спектральном анализе этой матрицы. Видно, что дополнение Шура являются операторно-значные регулярные функции, определенные вне спектров операторов
и они играют важную роль в спектральном анализе этой матрицы. Видно, что дополнение Шура являются операторно-значные регулярные функции, определенные вне спектров операторов ![]() и
и ![]() , соответственно. Дополнение Шура сначала использовано в теории матриц [1].
, соответственно. Дополнение Шура сначала использовано в теории матриц [1].
Термин «дополнение Шура» было введено в работе [2].
Через ![]() обозначим
обозначим ![]() -мерный куб с соответствующим отождествлением противоположных граней. Пусть
-мерный куб с соответствующим отождествлением противоположных граней. Пусть ![]() – одномерное комплексное пространство,
– одномерное комплексное пространство, ![]() – гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на
– гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на ![]() и
и ![]() – гильбертово пространство квадратично- интегрируемых (комплекснозначных) функций, определенных на
– гильбертово пространство квадратично- интегрируемых (комплекснозначных) функций, определенных на ![]() .
.
В гильбертовом пространстве ![]() рассмотрим следующую блочно- операторную матрицу
рассмотрим следующую блочно- операторную матрицу
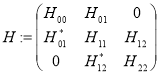 (1)
(1)
с матричными элементами
![]() ,
, ![]()
![]() ,
, ![]() ,
,
![]()
Здесь ![]() — фиксированное вещественное число,
— фиксированное вещественное число, ![]() – вещественнозначные непрерывные функции на
– вещественнозначные непрерывные функции на ![]() , а
, а ![]() – вещественнозначная непрерывная функция на
– вещественнозначная непрерывная функция на ![]() .
.
В этих предположениях на параметры оператор ![]() , действующий в гильбертовом пространстве
, действующий в гильбертовом пространстве ![]() по формуле (1), является ограниченным и самосопряженным. При этом
по формуле (1), является ограниченным и самосопряженным. При этом ![]() сопряженный оператор к
сопряженный оператор к ![]() и
и
![]()
Наряду с оператором ![]() в гильбертовом пространстве
в гильбертовом пространстве ![]() рассмотрим еще блочно- операторную матрицу размера
рассмотрим еще блочно- операторную матрицу размера ![]() :
:
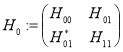
Далее, пространство ![]() представим в виде ортогональной суммы гильбертовых пространств
представим в виде ортогональной суммы гильбертовых пространств ![]() и
и ![]() . Тогда второе дополнение Шура
. Тогда второе дополнение Шура ![]() блочно-операторной матрицы
блочно-операторной матрицы ![]() , соответствующее разложению
, соответствующее разложению ![]() , определяется следующим образом
, определяется следующим образом
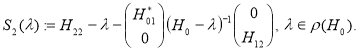
После простых вычислений имеем, что
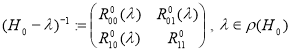
где
![]()
![]()
![]()
![]()
Имеют место следующие утверждение.
Утверждение 1. Число ![]() является собственным значением оператора
является собственным значением оператора ![]() тогда и только тогда, когда оператор
тогда и только тогда, когда оператор ![]() имеет собственное значение, равное нулю и их кратности совпадают.
имеет собственное значение, равное нулю и их кратности совпадают.
Утверждение 2. Пусть ![]() . Тогда
. Тогда ![]() . Из утверждений 1 и 2 вытекают следующие
. Из утверждений 1 и 2 вытекают следующие
Следствие 1. Пусть ![]() . Тогда
. Тогда ![]() .
.
Следствие 2. Пусть ![]() . Если
. Если ![]() (соот.
(соот. ![]() ) при некотором
) при некотором ![]() , то существует число
, то существует число ![]() такое, что
такое, что ![]() (соот.
(соот. ![]() ).
).
Литература:
- Schur. Uber potenzreihen, die im innern des einheitskreises beschr¨ankt sint. J. Reine Angew. ¨ Math., 147 (1917), 205–232.
- E. V. Haynsworth. Determination of the inertia of a partitioned Hermitian matrix. Linear Algebra Appl., 1:1 (1968), 73–81. 2

