Пусть ![]() , измеримая
, измеримая ![]() -периодическая функция
-периодическая функция ![]() . Множество всех измеримых,
. Множество всех измеримых, ![]() - периодических функций
- периодических функций ![]() для которых
для которых
![]() ,
,![]() ,
,
называют весовым пространством Лебега и обозначается![]() . В этом пространстве норма вычисляется
. В этом пространстве норма вычисляется
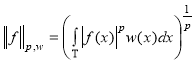 .
.
Пусть ![]() . Весовая функция
. Весовая функция ![]() , если существует число
, если существует число ![]() такая, что для любого интервала
такая, что для любого интервала ![]() выполняется неравенство
выполняется неравенство
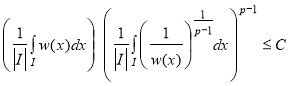 ,
,
где ![]() — длина интервала
— длина интервала ![]() .
.
Если ![]() , то положим
, то положим
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]()
Для функции
![]() ,
,![]() .
.
Известно, что ![]() - неотрицательная, неубывающая, непрерывная функция и
- неотрицательная, неубывающая, непрерывная функция и
![]() ,
,![]() .
.
Пусть ![]()
![]() - множество тригонометрических полиномов порядка не выше
- множество тригонометрических полиномов порядка не выше ![]() . Наилучшее приближение функции
. Наилучшее приближение функции ![]() множеством
множеством![]() определяется по формуле
определяется по формуле
![]() ,
,![]()
Известно следующее утверждение.
Теорема 1 ([2]). Пусть ![]() ,
,![]() и
и ![]() ,
, ![]() . Тогда для функции
. Тогда для функции ![]() справедлива оценка
справедлива оценка
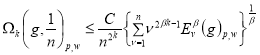 .
.
Далее, рассмотрим пространство ![]() в случае
в случае ![]() ,
,![]() ,
, ![]() и
и ![]() обозначим как
обозначим как ![]() .
.
Теорема 2 ([3, с.46]). Пусть ![]() ;
; ![]() . Если
. Если ![]() ,
,
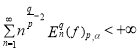 ,(1)
,(1)
то![]() имеет место неравенство
имеет место неравенство
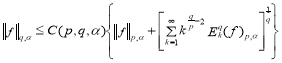 .(2)
.(2)
Замечание. В случае ![]() теорема 2 доказана П. Л. Ульяновым [4,с.104].
теорема 2 доказана П. Л. Ульяновым [4,с.104].
Теорема 3. Пусть ![]() ,
,![]() . Если
. Если ![]() и выполнено условие (1) то
и выполнено условие (1) то ![]() и
и
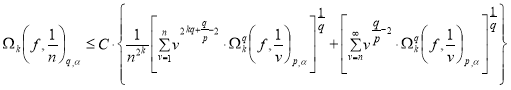 .(3)
.(3)
Доказательство. Пусть ![]() и выполнено условие (1). Тогда по теореме 1 функция
и выполнено условие (1). Тогда по теореме 1 функция ![]() . Докажем оценку (3). По теореме 1 и неравенству (2) имеем
. Докажем оценку (3). По теореме 1 и неравенству (2) имеем
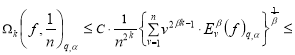
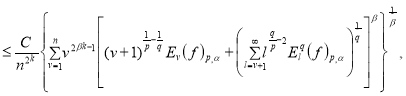 (4)
(4)
где ![]() .
.
Применяя неравенство ![]() ,
, ![]() ,
, ![]() имеем
имеем
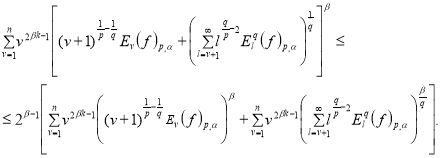 (5)
(5)
В силу оценки
![]()
из неравенств (4) и (5) получим
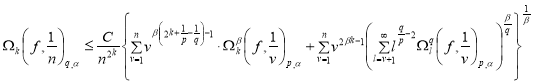 . (6)
. (6)
Если ![]() , то меняя порядок суммирования имеем
, то меняя порядок суммирования имеем
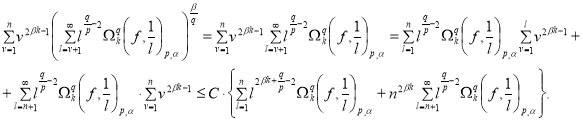
Поэтому из неравенства (6) получим
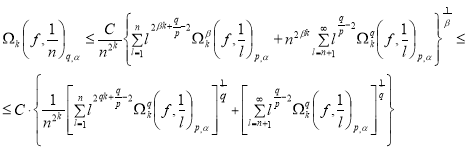
в случае ![]() , т.е
, т.е ![]() .
.
Литература:
- Muckenhoupt B. Weighted Norm Inequalities for the Hardy Maximal Function,Trans.Amer.Math.Soc. -1972, № 165.- P.207–226.
- Guven A., Israfilov D. M. Improved Inverse Theorems in Weighted Lebesgue and Smirnov Spaces.Bull.Belg.Math.Soc.Simon Stevin.- 2007, № 14.- P.681–692.
- Смаилов Е. С., Каримов С. К. Весовые аналоги одной теоремы вложения П. Л. Ульянова // Сб.Математические исследования. — Караганда, 1976.-Вып. 3.- C. 46–50.
- Ульянов П. Л. Теоремы вложения и соотношения между наилучшими приближениями (модулями непрерывности) в разных метриках //Мат.сб., 1970.- Т.81.- № 1.- C.104–131.







