The goal of education system in the Republic of Kazakhstan to develop the education and scientific system of state programs for 2016-2019 years – on the basic of teaching with new method will give the deep knowledge and professional expertise in according with the requirement functional literacy, directing the special attention to self-development and make the right decision by yourself. Personal ability will be seen by his opportunities that he is making the certain action and the opportunities lead the person to create the successes and achievements.
At the decision of geometric drawn tasks the relations between the action of pupils’ minds and components have to skills such as spatial, logical, metrical, intuitional, constructive and symbolical. Besides with appropriate school geometry course on the notional-methodical direction they have to know the methods how solving the tasks and selecting the efficient methods of opportunities and using the different ways, the pupils must widely to realize the inner and intermediate subject connections.
The pupils are deciding the geometric drawn tasks is formed the notion about different geometric figures and their transformation opportunities, imagine the geometric figures through the methods and giving tasks they can work by mentally, finding the way is developed their possibilities, because the geometric figures are represented exact models in the environment, teaching the geometry gives more opportunities through the figures to control with eyes, compare, assume, make the certain projects.
Solving the drawn tasks, pupils get used to decide the task in series and the simple draw task will strengthen and deepen their geometric theoretical knowledge. However, nowadays when the pupils solve drawn tasks we see in our experience work that they couldn’t decide the geometric exercises and difficulties among them. Noticeably, the pupils not fully assimilated the methods and processes of solving drawn task. That’s why when we teach the pupil how to solve drawn task I want to enter own share to develop the geometrical exercises.
Generally it takes the main role to solve drawn tasks and developing pupils’ constructive abilities and give to understand well the theoretical materials. Help to develop the pupils’ logic, ability to think, constructive abilities and formed their graphical methods. That’s why with the view of practice we have to teach them right methods of solving the unviable and nonstandard drawn tasks. On the process of solving drawn tasks first of all not to draw the searching figure thorough the given picture or figure elements, have to imagine the exact it and with its elements we have to outline in mind. During the solve drawn task without drawing tools it will develop measuring through eyes and to account the exact movement.
Solving drawn task first of all it is not draw the figure, we have to say the pupils how draw it, make proper arguments and substantiate it. When we show them the method and explain how drawn geometric task, we can say that it solved. After it in the result of drawn geometric task, we have to demonstrate need figure.
Besides, one of the problem solving the drawn task – it is formed the skills of pupils’ solving the drawn task and the difficulties to learn them to image it, because haven’t the rooted consistent theories and methods in solving drawn task, solve drawn task containment to the mind of pupils. That’s why during the solve drawn tasks followed by four step scheme:
1) Analyze. In this period prepare to solve drawn task, determine the way how to solve the drawn task, so on the condition of task the given figure is considered it is drawn and it is drawn before. It is for pupils additional or auxiliary drawing. Through this additional or auxiliary drawing we want to solve the drawn task.
2) Drawing. In drawing period we have to draw the satisfied drawing figure and make the way of drawing.
3) Argue. In this period the selective figure that satisfied full task and make sure and agued.
4) Through research the selective method is always possibly, we can see how much ways to solve drawn task.
1-task. One of the side and close angle to this side and by combined last two sides have to draw the triangle.
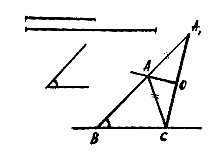Analyze. We are drawn ∆ ABC triangle. We image that mark the point B and C. So we have to find the top of A. First, is given ABC triangle that’s why point A lying on the ray BA. Second, a length is equal of combine sides of AB and AC and the rapture will be the top of line. To BA extended line is equal the length of side AC is equal and draw AA1 segment. Then by draw two sides and between angle we can draw the A1BC triangle. In isosceles triangle A1AC the side of average perpendicular A1C intersects the ray BA1 in point A.
Drawing. 1) To given angle draw the equal angle.
2) we draw the segment to the one side BC (given side), to the second side BA1=AB+AC (the equal segment for two combined sides).
3) Draw ∆BA1C triangle.
4) Draw the middle perpendicular of A1C side. The intersection ray of BA point we sign it with letter A. ∆ BAC search triangle.
Argue. In the triangle ∆ BAC when we draw the one side is equal to given side; two sides combine are equal to segment; between angle is equal to given angle.
Research. With two sides and between angle we can draw the A 1 BC triangle and it will be one, can draw the middle perpendicular of A1C side and it will be one too, the middle perpendicular’s intersection point with BA1 ray will be one too. So, the one way to solve the task.
2-task. Through the side AB, height CH and angle A draw the ∆ ABC triangle, here AB=P 1 Q1, CH= P 2 Q2, 
A=hk.
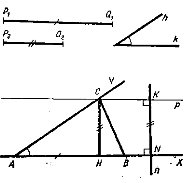Analyze. We think will draw the ∆ABC triangle such as AB=P1Q1, CH= P2Q2, 
A=hk. Farther it’s not difficult to draw the side AB and equal to given angle BAY. If we want to draw the point C will make the two conditions. 1) point C belongs to AC ray; 2) point C from AC ray has to distance P2Q2. So searching point C is an intersection point of straight AY and p.
Draw. 1. Angle XAY =hk and ray AX to this line from point A is equal to P1Q1 segment we draw equal segment.
2. To straight line AX we lined the perpendicular line n. So point N will be intersection point of the line AX and n.
3. to the line of n from point N as equal to the segment P 2 Q2 we measured and drawn NK segment.
4. Through point K to line AX we draw the parallel p line. p line intersected point C on the ray AY.
5. Lining the BC segment and draw the searching ∆ABC angle.
Argue. Drawn angle ∆ ABC is satisfied the condition of task. Actually drawing AB=P1Q1, CH= P2Q2, A=hk, besides all points of line p from line AB lying the distance P2 Q2.
Research. Researching angle ∆ABC can draw with any given information. More polygons of satisfying task. All these angles are equal each to each, that’s why only one answer of task.
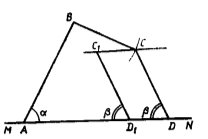
3-task. Three sides and to fourth side draw by adjacent two angles foursquare.
Draw. From any MN line mark A and D1 points. Connecting these points as a top α and β angles we draw the equal angles. For these laterally sides draw from given foursquare is measuring the AB=c and D1C1 sides. By point C draw the parallel straight line to the MN line and from point radius a that side is equal we draw the arc that intersecting the MN line. So will take top C from researching foursquare. Through top C we draw CD || C 1 D1 segment. ABCD – our research foursquare.
I suggest the following draw tasks to develop skills and logic of pupils as appoint task:
1 task. Given the ∆ABC angle. The top D not matching with top B draw the angle as equal ∆ADC angle.
Draw.
2 task. Side BC, angle B and through bisector of his top B draw the side ∆ ABC.
3 task. AB, BC sides and carries out through median from these AB, BC sides draw the angle.
4 task. The angle in the top A angle will be arc angle given ∆ABC angle. Draw the point M will be equal MA=MB in the BC side.
5 task. Hypotenuse BC and through the angle in the angle B draw ABC right triangle.
6 task. Through B arc angle and BD bisector draw ABC right triangle.
References:
- The state program for 2016-2019 years to develop education system and scientific in the Republic of Kazakhstan (№205 order from 1 March 2016).
- 25 April 2015 year №327 Decree of Government of Republic of Kazakhstan about to amend and supplement from 23 August 2012 year №1080 Decree of Government of Republic of Kazakhstan «To affirm obligation standardization of education to all state appropriate degree in the education system».
- Shynybekov A.N., Geometry, The subject for grade 7 to general education in the school, Almaty, Atamura, 2012.
- Shynybekov A.N., Geometry, The subject for grade 8 to general education in the school, Almaty, Atamura, 2012.
- Shynybekov A.N., Geometry, The subject for grade 9 to general education in the school, Almaty, Atamura, 2013.
- Shynybekov A.N., Methods of educate geometry, The subject for grade 9 of teachers’ to general education in the school, Almaty, Atamura, 2013.
- Atanasyan L.S., Poznyak E.G., Butuzov V.F., Geometry, 6-8 grade, Education Moscow, 1981.
- Petrakov I.S., Matematical coterie, 8-10 grade, Education Moscow, 1987.
