Компьютеры — это калькуляторы с большими вычислительными возможностями. Арифметические задачи они могут выполнять очень быстро: например, просуммировать заданные данные для подсчета ежедневных продаж, посчитать проценты налогов и вывести необходимые графики, удобные для понимания человеку «со стороны».
Чтобы человек мог посмотреть фильм онлайн или прослушать музыку из интернета, компьютеру требуется ничего более чем выполнение арифметических операций, схожих с теми, что проходят в школе. Выполнение арифметических операций компьютером происходит поразительно быстро, человеческий мозг в большинстве случаев сильно уступает в скорости их обработки.
Но что насчет других задач? К примеру, мы хотим опознать, что показано на изображении. Человек очень быстро распознает, что это изображение содержит. Но, простейшая задача для нас оказывается довольно сложной для компьютера.
Чтобы решить данную задачу компьютеру, необходим алгоритм. Здесь на помощь и приходят алгоритмы для решения задач искусственного интеллекта.
В целом, мы хотим от компьютера: подать ему на вход какие-то данные и получить на выходе решение нашей задачи, например:
На рисунке 1 покажем это визуально.
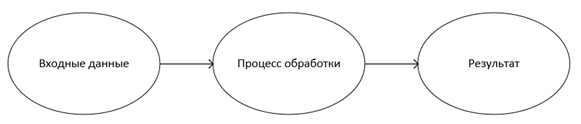
Рис. 1. Процесс получения результата от компьютера
Например, мы хотим узнать, сколько будет 
, рисунок 2 показывает процесс обработки:
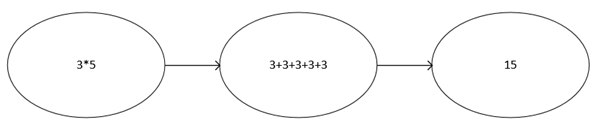
Рис. 2. Пример расчета произведения с помощью компьютера
А теперь представим, мы хотим перевести метры в километры, но формулы, по которой можно провести расчеты мы не знаем, а знаем лишь, что отношения между метрами и километрами линейное. Что делать в данном случае?
Знание вида отношения между километрами и метрами дает нам подсказку, мы знаем, что километр = 
,
где N — это какая-то константа.
Другой подсказкой будут являться несколько правильных примеров с корректными значениями километров.
|
Правильное отношение |
Метры |
Километры |
|
1 |
1540 |
1.54 |
|
2 |
2980 |
2.98 |
Что делать дальше? Дальше необходимо выбрать случайную константу N.
Допустим, N = 
Пробуем подставить данное значение: 1.54 = 1540/900 = 1.71.
Мы получили примерно 1.71, но правильным ответом является 1.54. Мы ошиблись на 0.17.
Ошибка = выходное значение — полученное = 1.54–1.71 = -0.17. Но что же делать дальше? Известно, что есть ошибка и известно её значение. Необходимо подкорректировать N. Исходя из ошибки в размере 0.17 в большую сторону, необходимо уменьшить N. Пробуем взять N = 
.
1.54 = 1540/950 = 1.62105263. Ошибка стала меньше. Но все еще недостаточно.
Подобными рассуждениями вполне реально прийти к необходимому числу (
)
Это и было простейшим примером обучения нейронной сети. Мы последовательно «улучшали» наше значение, пока не пришли к необходимому. Данный процесс называется итеративным.
Такую задачу можно представить также графически, где имеются данные о длине и ширине, например, крыс и змей. Как не сложно догадаться, красным изображены змеи, а зеленым — крысы.
Другой вопрос, что же в данном случае будет являться параметром N из предыдущей задачи? В этом случае — это будет прямая разделяющая две данные выборки, и задачей теперь будет провести эту линию под наклоном, наиболее правильно разделяющим выборки.
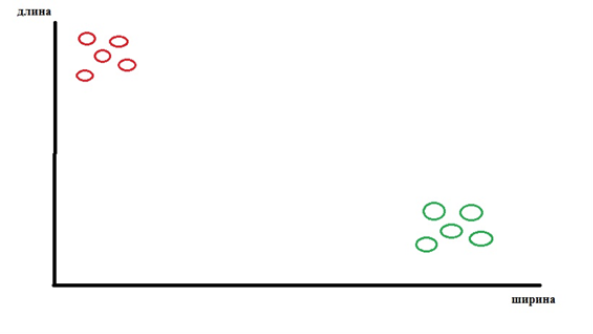
Рис. 3. Отображение на графике крыс и змей по длине и ширине
Допустим, сначала мы выбрали случайную линию, разделяющие две выборки. Как видно из рисунка 4 — эта линия очень плохо делит наши выборки.
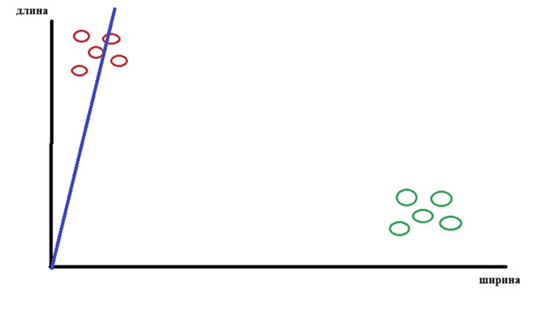
Рис. 4. Пример изначального разделения
После определенного количества вычислений, аналогичных предыдущему примеру, будет получена линия, близкая к той, что изображена на рисунке 5.
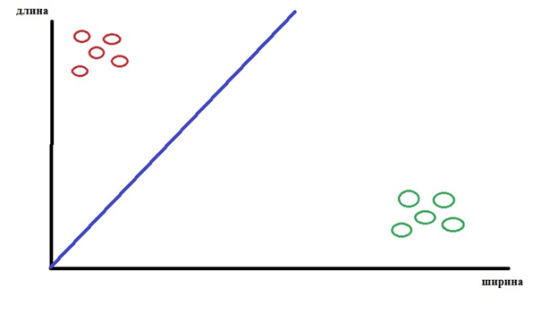
Рис. 5. Пример более верного разделения
Для классификации нового элемента — вводим элемент, согласно его ширине и длине и определяем — крыса это или змея.
Но снова появляется вопрос, а достаточно ли для всех задач «провести одну линию» или же нужно больше?
Для ответа на данный вопрос можно обратиться в любую книгу по нейронным сетям и посмотреть примеры классификации логических функций (or, and, xor) и убедиться, что, к примеру, для xor уже нужно минимум 2 разделяющих линии.
Чтобы понять, как работает искусственный нейрон необходимо рассмотреть простейший пример естественного нейрона. Функция нейронов — передача сигналов от одного к другому через аксоны к концевым ветвям аксона (терминалям). Таким образом, мы получаем различные сигналы от наших глаз, ушей, рук, которые проходят по нашей нервной системе и идут к мозгу. Также стоит отметить, что входной сигнал генерирует выходной только лишь при условии, если его сила достаточна для минимума. Данное свойство называется пороговым значением. Выходной сигнал генерируется с помощью функции активации.
В искусственных нейронных сетях в качестве функции активации можно использовать, например, функцию-сигмоиду (также может называться логистическая функция). Ее формула имеет следующий вид [2]:
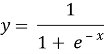
Где х — это входной сигнал.
Если сигнал не один, а их, к примеру, четыре, то х = a + b + c + d,
Где а, b, c, d — входные сигналы
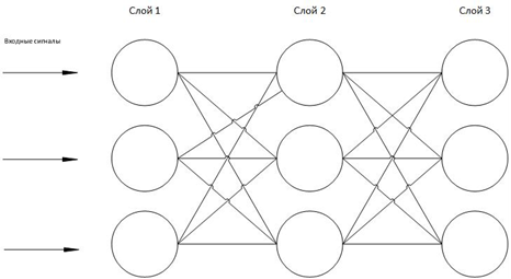
Рис. 6. Графическое представление искусственной нейронной сети
На рисунке 6 видно, что имеется 3 слоя, в каждом по 3 нейрона. Нейроны связаны между собой «каждый с каждым». У каждой связи имеется определенный вес.
Из рисунка 6 приведем пример. Допустим, входные сигналы равны соответственно 1, 2, 1. Связи w11, w12, w13 исходят из первого нейрона, w21, w22, w23 из второго и w31, w32, w33 из третьего. Допустим w11=w21=w31 = 0.5, w12=w22=w32=0.7 и w13=w23=w33=0.4.
Тогда для первого нейрона во втором слое
Далее применяем сигмоидную функцию к получившемуся х = 2 и получаем 
Аналогичным образом рассчитываются значения для двух других нейронов, и получившиеся значения используются для подсчета в следующем проходе, где веса w11, w12, w13 и так далее уже другие.
В конце получается три выходных значения. Что дальше? Далее выходные значения используются для проверки с тренировочными примерами. Необходимо скорректировать выходные значения, сравнивая с «эталонными» примерами.
Остается нерешенным вопрос распределения ошибки между нейронами, когда мы пытаемся настроить выходной результат, близкий к оптимальному.
На рисунке 7 графически показано, что под этим подразумевается [1].
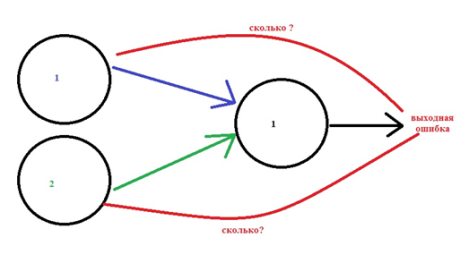
Рис. 7. Определения распространения ошибки
Количество ошибки на рисунке 7 распределяется согласно весам (w11, w21), сделавшим вклад в получение значения.
Получается, что ошибка распределяется следующим образом:
E11 = 
E21 = 
Сразу понятно, что выходная ошибка равна сумме Е11 и Е21.
Ошибку можно рассчитывать различными способами, например:
Ошибка = целевое — получившееся
Ошибка = 
Ошибка = 
Получается, что помимо простого вычитания, можно использовать абсолютное значение, а также квадрат разности. Имеются и другие способы.
Перепишем расчет ошибки в ином виде [1]:
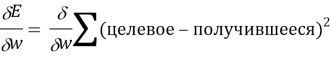
Применим к данной функции правило дифференцирования сложной функции (Chain Rule) [1]:
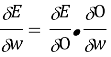
Где O — выходное
Далее t — целевое
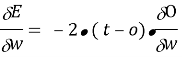
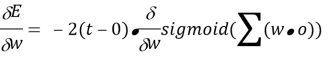
Остается вопросом, как продифференцировать сигмоиду [1]:
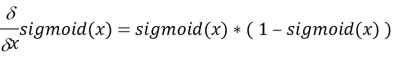
Таким образом, конечное выражение приходит к виду:
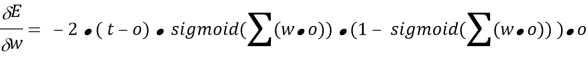
Таким получилось выражение. Двойку вначале можно отбросить, поскольку в данном случае константа нас не интересует.
Изменение весов выражено следующим выражением:
Где 
- это скорость обучения. Это регулируемый параметр, который необходимо подбирать для каждой задачи.
В последнем выражении мы получили регулирование весов с помощью метода градиентного спуска.
Литература:
- Kriesel D. A brief introduction to Neural Networks [Электронный ресурс], 2007. 286 p. [http://www.dkriesel.com/en/science/neural_networks].
- Hagan M., Demuth H., Beale M., De Jesus O. Neural Network Design New York: Martin T. Hagan and Howard B. Demuth, 2014. 1012 p.
- Барсегян А. А., Куприянов М. С., Степаненко В. В., Холод И. И. Методы и модели анализа данных: OLAP и Data Mining. СПб.: БХВ-Петербург, 2004. 336 с.
