Рассмотрен приближенный метод расчета шарнирно связанных двух балок, лежащих на упругом неоднородном основании при действие произвольной распределенный нагрузки.
С помощью прерывателей Герсеванова распределённая нагрузка представлена в самом общем виде. Получено выражение для упругой линии балки при действии произвольной распределённый нагрузки как угодно расположенный по балке W.
Рассмотрим составную балку связанными между собой шарнирами и лежащую на упругом неоднородном основании, модуль деформации которого изменяется по закону![]()
![]() (1)
(1)
и при действии произвольной распределенной внешней нагрузки (рис.I.а).
Для решения задачи составная балка освобождается от шарнирных связей, при этом получается ряд балок конечной длины и постоянного поперечного сечения.
Каждая балка будет находиться под действием неизвестных реакции связи Y1 возникающие в местах отчленения одной балки от другой и заданных внешних нагрузок, которое выразится в самом общем виде через функциональные прерыватели Герсеванова [2] (рис.I.б, начало координат берем на левых концах балок, положительные абсциссы вправо, координаты вниз).
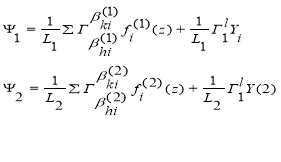
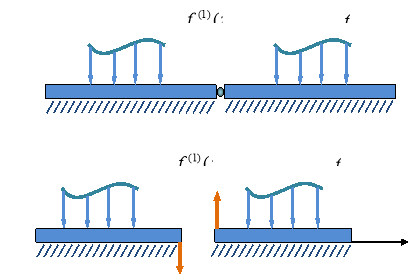
Рис. I.
Такая расчетная схема дает возможность каждую из полученных отдельных балок рассмотреть и рассчитать, как простую балку конечной длины и постоянного поперечного сечения, лежащую на упругом неоднородном основании. Каждой отсеченной балке не учитываем её поперечные деформации по высоте сечения, а грунт основания под каждой балкой принимаем разным и рассматриваем как сплошную упругую неоднородную среду, характеризуемую модулем деформации изменяющимся с глубиной по закону (1). При этом неоднородность грунта-основания учитывается, и по горизонтали, и по вертикали. Следуя [2], характер распределения реактивных давлений грунта под балками принимаем в таком виде:
![]() (3)
(3)
![]() (4)
(4)
Для каждой балки составляем соответствующее дифференциальное уравнение изогнутой оси
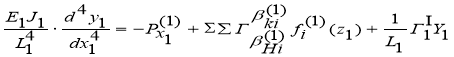 (5)
(5)
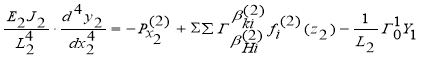 (6)
(6)
Для деформации грунта под каждой отсеченной балкой используем уравнения осадки поверхности неоднородного полупространства, работающих в условиях плоской задачи (плоская деформация).
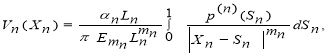 (7)
(7)
где n=1,2
После четырехкратного интегрирования системы дифференциальных уравнений (5) и (6) получим соответствующее обще уравнение упругой линии каждой балки:
![]()
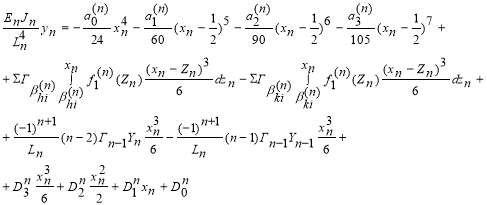
где n = 1, (8)
В уравнениях (8) в каждое из них входят по восемь неизвестных величин (по четыре параметра и по четыре произвольные постоянные интегрирования). Для нахождения этих искомых величин для каждой балки используем по восемь следующих условий: два условия статики; два граничных условия; четыре условия прилегания балки к основанию, которые легли в основу для вывода расчетных формул в [4].Используя все перечисленные выше условия и с учетом формул выведенных в [4], находим искомые параметры для всех отсеченных балок:![]() Формулы для параметров n-й балки имеют вид:
Формулы для параметров n-й балки имеют вид:
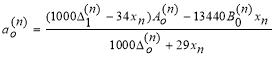
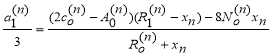
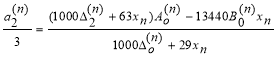
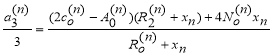 (9)
(9)
Где
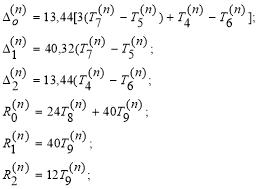
Где ![]() определяются согласно [4].
определяются согласно [4].
Вспомогательные члены
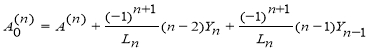
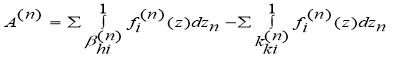
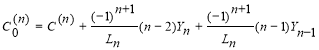
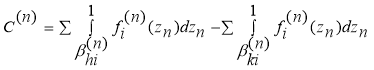
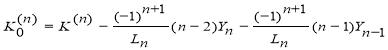
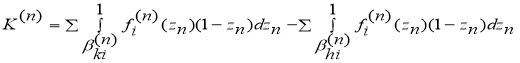
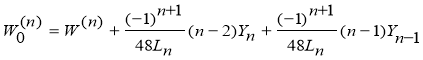
![]()
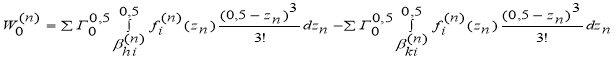
![]()
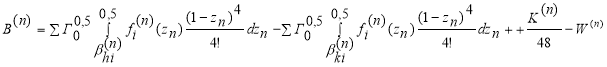
![]()
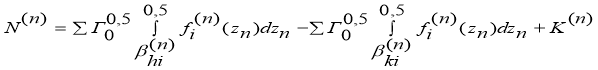 (10)
(10)
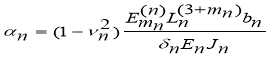 -
-
показатель гибкости n-ой балки. Где ![]() I,2В этих формулах приняты следующие обозначения:
I,2В этих формулах приняты следующие обозначения:
![]() - реактивное давление грунта на n — ную балку;
- реактивное давление грунта на n — ную балку; ![]() — Произвольная какая угодно распределенная нагрузка на n — ую балку; Yn- Пока неизвестная поперечная реакция возникающие по концам n — ой балки расчет расчленения соседних балок,
— Произвольная какая угодно распределенная нагрузка на n — ую балку; Yn- Пока неизвестная поперечная реакция возникающие по концам n — ой балки расчет расчленения соседних балок, ![]() — без размерная абсцисса в рассматриваемом сечении n — ой балки, bn — Ширина n-й балки;Ln — длина n -й балки:
— без размерная абсцисса в рассматриваемом сечении n — ой балки, bn — Ширина n-й балки;Ln — длина n -й балки: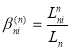 Безразмерное расстояние от левого концаn — ой балки до начала распределенной нагрузки
Безразмерное расстояние от левого концаn — ой балки до начала распределенной нагрузки ![]() ;
;![]() — Модуль деформация грунта на глубине Yn = l под n-й балкой; Von — Коэффициент Пуассона n-й балки; жестокость n-й балки;
— Модуль деформация грунта на глубине Yn = l под n-й балкой; Von — Коэффициент Пуассона n-й балки; жестокость n-й балки;
В формулах, по которым определяется искомые параметры, входит неизвестная реакцияY1возникающие по концам смежных балок, то для получения замкнутой системы уравнений к восьми условиям добавляем условия сопряженности: реакция грунта на балку со стороны основания в местах мысленного отсечения одной балки от другой были равными между собой.
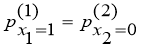
![]() (11)
(11)
Согласно (9), параметры для первой балки определяется по формулам:
![]()
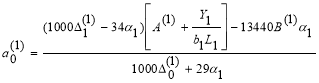
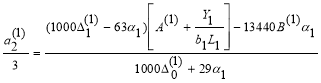
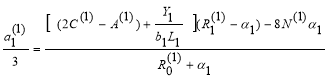
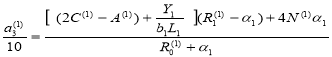
(12)
![]() Параметры для второй балки:
Параметры для второй балки:
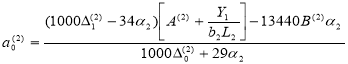
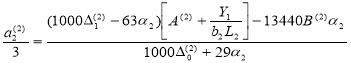
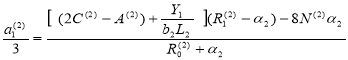
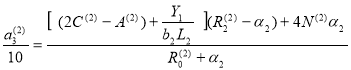 (13)
(13)
Где, b2 — ширина рассматриваемых балок
Поставляя значения параметров![]() из формул (12), (13) в (11) и преобразовав его, получим следующее линейное алгебраическое уравнение:
из формул (12), (13) в (11) и преобразовав его, получим следующее линейное алгебраическое уравнение:
![]() (14)
(14)
В уравнению (14) приняты следующие обозначения
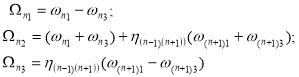 (15)
(15)
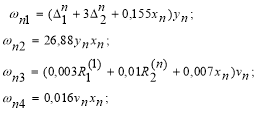 (16)
(16)
![]() (17)
(17)
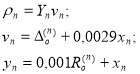 (18)
(18)
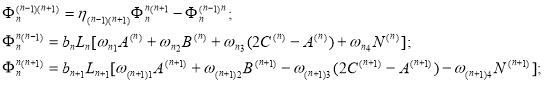
(19)
Определяя значение Y1 из (14) подставляя (12), (13) в (3), (4) и (8), можно получить реактивные давления, поперечную силу, изгибающий момент, угол поворота сечений и упругую линию балки, лежащей на неоднородном основании при действии произвольной распределенной нагрузки.
Литература:
- Клейн Г. К. Учет неоднородности, разрывности деформаций и других механических свойств грунта при расчете сооружений на сплошном основании. Сб. трудов № 14, МИСИ, М., 1956г.
- Симвулиди И. А. Расчет инженерных конструкций на упругом основании. Изд-во «Высшая школа», М.,1978г.
- Ширинкулов Т. Ш. Расчет инженерных конструкций на упругом неоднородном основании. Изд-во «Фан», Ташкент,1970г.
- Турабов Х. Ш. Расчет балочных плит, лежащих на упругом непрерывно неоднородном основании. Тезисы докладов областного семинара-совещания (май-1988г) г.Самарканд-1988г.

