Частично интегральные операторы встречаются в квантовой теории поля, физике твердого тела, а также в механике сплошных сред, аэродинамике и других областях физики и механики.
Пусть ![]() – мера Лебега в
– мера Лебега в ![]() и
и ![]() – гильбертово пространство квадратично интегрируемых функций на
– гильбертово пространство квадратично интегрируемых функций на ![]() . В настоящей работе рассмотрим частично интегральный оператор
. В настоящей работе рассмотрим частично интегральный оператор ![]() , заданный следующим образом:
, заданный следующим образом:
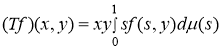 .
.
Оператор ![]() является линейным ограниченным и самосопряженным оператором в
является линейным ограниченным и самосопряженным оператором в ![]() .
.
Обозначим через ![]() соответственно спектр, существенный спектр, дискретный спектр соответственно.
соответственно спектр, существенный спектр, дискретный спектр соответственно.
Следует отметить, что в работе [1,2] в качестве операторов возмущения рассматриваются частично интегральные операторы типа ![]() . Там предполагаются, что частично интегральные операторы являются положительными и принадлежат пространству операторов со следом. Этот факт используется при построение соответствующего уравнения типа Фаддеева для собственных функций.
. Там предполагаются, что частично интегральные операторы являются положительными и принадлежат пространству операторов со следом. Этот факт используется при построение соответствующего уравнения типа Фаддеева для собственных функций.
Вместе с оператором ![]() рассмотрим семейство компактных операторов
рассмотрим семейство компактных операторов ![]() действующих в гильбертовом пространстве
действующих в гильбертовом пространстве ![]() по следующим правилам:
по следующим правилам:
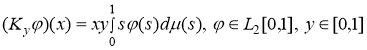 .
.
Отметим, что спектр и числовая образ одного интегрального оператора типа ![]() изучены в работе [3].
изучены в работе [3].
Теорема 1. Число нуль принадлежит существенному спектру оператора ![]() .
.
Доказательство. Для каждой точки ![]() оператор
оператор ![]() является компактным оператором в
является компактным оператором в ![]() . Пусть
. Пусть ![]() фиксирована. Ввиду компактности оператора
фиксирована. Ввиду компактности оператора ![]() существует последовательность ортонормированных функций
существует последовательность ортонормированных функций ![]() из
из ![]() таких, что
таких, что ![]() . Для каждого
. Для каждого ![]() определим множество
определим множество
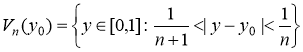 .
.
Рассмотрим последовательность ортонормированных функций
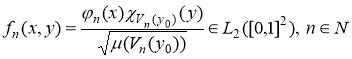 ,
,
где ![]() – характеристическая функция множества
– характеристическая функция множества ![]() . Пусть
. Пусть ![]() – частично интегральный оператор в
– частично интегральный оператор в ![]() с ядром
с ядром ![]() , т. е.
, т. е.
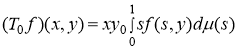 .
.
Тогда
![]() .
.
С другой стороны,
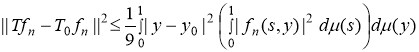 .
.
В силу непрерывности функции ![]() на
на ![]() при достаточно малом
при достаточно малом ![]() существует достаточно большое число
существует достаточно большое число ![]() такое, что
такое, что
![]() для всех
для всех ![]() .
.
Тогда ![]() для всех
для всех ![]() , т. е.
, т. е. ![]() . Следовательно, из неравенства
. Следовательно, из неравенства ![]() вытекает, что
вытекает, что ![]() , и поэтому
, и поэтому ![]() . Теорема 1 доказана.
. Теорема 1 доказана.
Из замкнутости существенного спектра самосопряженного оператора вытекает следующая теорема.
Теорема 2. Дискретный спектр оператора ![]() отсутствует, т. е.
отсутствует, т. е.
![]() .
.
Аналогично, если рассмотрим частично интегральный оператор ![]() , заданный следующим образом:
, заданный следующим образом:
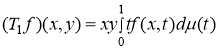 ,
,
то справедливы следующие теоремы.
Теорема 3. Число нуль принадлежит существенному спектру оператора ![]() .
.
Теорема 4. Дискретный спектр оператора ![]() отсутствует, т. е.
отсутствует, т. е.
![]() .
.
Литература:
- M. I. Muminov, T. H. Rasulov. The Faddeev Equation and Essential Spectrum of a Hamiltonian in Fock Space. Methods of Functional Analysis and Topology. 17:1 (2011), 47–57.
- Т. Х. Расулов, А. А. Рахмонов. Уравнение Фаддеева и местоположение существенного спектра одного трехчастичного модельного оператора. Вестник Самарского государственного технического университета, Серия физико-математические науки, 23:2 (2011), 170–180.
- Н. Х. Шарипова, Х. Ж. Акрамова, З. Ф. Исомова. Спектр и числовая образ одного интегрального оператора. Молодой учёный. 2017, № 4 (138), С. 120–122.

