В данной статье рассматривается метод восстановления простых функций, сохраненных в виде p-файлов, средствами MATLAB. В качестве основного инструмента используется встроенный отладчик и функция dbstop. Применение описанных в статье методов позволяет восстановить утраченные исходные коды простых линейных и итерационных функций.
MATLAB позволяет сохранить откомпилированные М-функции в виде p-кода [1]. В таком случае в дальнейшем функция будет представлять собой “чёрный ящик”: пользователь будет иметь дело только с введёнными им данными и с возвращаемым результатом. Однако в ряде случаев может потребоваться обращение к исходному коду функции. Например, исходный код, необходимый для работы, может быть утерян, а производить какие-либо изменения в коде функции, сохранённой в виде p-файла, не представляется возможным. В статье будет рассмотрен способ восстановления исходного кода функции по p-коду средствами MATLAB, не подразумевающими попытки вскрыть шифр либо алгоритм кодирования, используемые в данной среде для хранения откомпилированных функций. Описанный в данной работе метод основан на анализе данных, получаемых в результате работы с p-файлом в среде MATLAB, подборе значений, выявлении зависимостей.
В качестве аппроксимации неизвестной функции, заданной множеством значений аргумента и соответствующими им выходными значениями функции, может выступать многочлен, генерируемый на основе имеющихся пробных точек, но ошибка может быть весьма велика, а если функция принимает на вход вектор произвольной длины, то такая аппроксимация невозможна. Поэтому мы будем говорить о восстановлении исходной функции.
Прежде всего, необходимо выяснить, какие аргументы принимает функция, если это заранее не известно. Будем подавать аргументы разных типов, в т. ч. вектора, и наблюдать, как это влияет на результат [2].
Далее приступим собственно к восстановлению функции. Для решения поставленной задачи нам потребуется функция dbstop [3], позволяющая пошагово отлаживать функции. Использовать её можно следующим образом:
>> dbstop <имя функции> <номер строки кода для точки останова>
Как видно в примере, dbstop может иметь два аргумента, однако второй не является обязательным. Если не указать номер строки кода для точки останова, функция остановится на второй строке.
Если введённый номер строки кода превосходит длину функции, выводится следующее сообщение об ошибке:
Error using dbstop
You cannot set a breakpoint past the start of the last expression in the file.
Таким образом, путём подстановки разных значений можно выяснить длину кода функции в строках.
Далее, применяя всё ту же функцию dbstop, выясним, какие использованы переменные и каким образом изменяются их значения. Для этого сначала вызовем функцию dbstop для нашего файла, а затем вызовем саму целевую функцию для допустимого набора аргументов:
>> dbstop <имя функции>
>> <имя функции>(<аргументы>)
K>>
K>>
Переход к следующей строке кода осуществляется нажатием на клавишу F10. В окне Workspace появляются имена и значения переменных, пример такого окна представлен на Рис. 1. Некоторые закономерности можно выявить уже на этом этапе, обратив внимание на имена переменных, порядок их появления и изменения. Так, например, можно выяснить, где в функции присутствует цикл, значения каких переменных в его теле изменяются. Также можно выявить переменные-флаги и участки кода, выполнение которых зависит от значений этих флагов. Таким образом, отладка при помощи dbstop позволит найти циклические и условные конструкции, если они есть. Целесообразно пробовать подавать на вход разные наборы аргументов, чтобы охватить как можно больше предусмотренных в целевой функции вариантов их обработки. Кроме того, на последнем шаге обнаруживается переменная, в которую записывается результат, возвращаемый функцией.
Выход из режима отладки либо переход к следующей точке останова осуществляется нажатием на клавишу F5.

Рис. 1. Вид окна MATLAB во время отладки
Очевидно, полученная на предыдущих этапах информация не позволяет в полной мере восстановить исходный файл. Установив количество, имена, порядок обновления переменных, мы можем приступить к выявлению зависимостей между ними, то есть к восстановлению конкретных выражений, присваиваемых им. Получив все эти зависимости, мы решим поставленную задачу — восстановим исходную функцию.
Помимо наблюдения за пошаговым исполнением функции, режим отладки позволяет на любом шаге вручную изменять значения имеющихся переменных при помощи обычного присваивания. Используя эту возможность, будем выявлять зависимости между переменными. Для этого запишем значения всех переменных на интересующем нас шаге (целесообразно выбрать первое обновления значения интересующей переменной). Затем, изменяя значения других переменных, выясним, какие из них влияют на целевую переменную, то есть вероятнее всего присутствуют в присваиваемом ей выражении. Когда обнаружены все такие переменные, можно восстанавливать саму искомую формулу.
Проще всего обнаружить, какие переменные входят в искомую формулу в качестве слагаемых. Очевидно, изменение их значений влечёт за собой эквивалентное изменение значения целевой переменной. Аналогично находятся и свободные множители. Также несложно найти переменные, чья разность входит в формулу как множитель: если задать значения этих переменных равными, то целевая переменная всегда будет обращаться в ноль либо сохранит лишь часть, являющуюся свободным слагаемым. На этом же этапе выявляются и делители, если таковые имеются: деление на ноль даёт бесконечность (в MATLAB обозначается как Inf).
Сложнее обнаружить менее очевидные зависимости: множители, содержащие выражения из переменных в показателе степени, тригонометрические функции и т. д. Рассмотрим, как это можно сделать. Для линейных функций подобные выражения восстановить достаточно просто, поэтому мы будем говорить об итерационных функциях.
Целесообразно записывать значения искомого коэффициента от итерации к итерации. Чтобы найти такое значение, нужно результирующую переменную разделить на все известные сомножители (значения известных сомножителей должны быть актуальны для данного шага цикла, если это переменные). Далее будем искать зависимость между значениями искомого коэффициента. Если разность или отношение этих значений постоянны, то задача практически решена: остаётся выяснить, входят ли эти разности или отношения в формулу как значение некоторой переменной или представляют собой постоянное число. Проанализировать число можно при помощи вопросно-ответной системы WolframAlpha [4, 5], дающей возможность узнать, является ли данное число некоторой правильной дробью или степенью числа, результатом тригонометрической функции и т. д. Поэтому для большей точности необходимо использовать для вычислений формат записи чисел с большим количеством знаков — format long [6].
Если зависимость между коэффициентами неочевидна, можно снова пробовать искать входящие в множитель переменные оговоренными выше способами: ведь отдельные множители или выражения в скобках могут быть возведены в степень. Кроме того, можно при пошаговом выполнении цикла сбрасывать значения обновляющихся переменных на начальное, чтобы выяснить механизм их обновления и влияние на искомую формулу. При таком анализе переменных должна выявиться искомая формула.
Когда все значения уже найдены, испортить картину может подача на вход функции другого набора аргументов. Если ранее идеально совпадавшие целевая и составленная нами функции теперь дают отличные друг от друга результаты, значит, не учтено влияние какой-то переменной, например, отвечающей за длину входного вектора или хранящей индекс элемента этого вектора. Восстановив функцию в полном объёме, мы окончательно решим поставленную задачу.
Подведём итог, представив описанный алгоритм в виде схемы на Рис. 2.
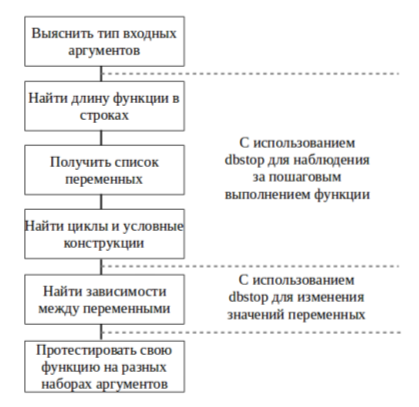
Рис. 2. Алгоритм восстановления функции
Следует отметить, что рассмотренный метод не даёт стопроцентной гарантии получения результата. Также неэффективен он и для восстановления длинных функций с большим количеством строк кода. Однако для небольших функций, как линейных, так и итерационных, имеющих условные конструкции и неочевидные формульные зависимости между переменными, такой способ восстановления даёт хорошие результаты. Разумеется, процесс восстановления долог и трудоёмок, однако других способов восстановить утерянный исходный код без декомпиляции не существует.
Литература:
- Создание Р-кодов MatLab // RADIOMASTER. URL: http://www.radiomaster.ru/cad/matlab/glava20/index20.php (дата обращения: 27.01.2017).
- В. Г. Потемкин «Введение в Matlab» // MATLAB.Exponenta. URL: http://matlab.exponenta.ru/ml/book1/matlab/chapter3/3_3.php (дата обращения: 27.01.2017).
- Set breakpoints for debugging // MathWorks. URL: https://www.mathworks.com/help/matlab/ref/dbstop.html (дата обращения: 1.02.2017).
- WolframAlpha // Wikipedia. URL: https://ru.wikipedia.org/wiki/WolframAlpha (дата обращения: 28.01.2017).
- Mathematics // WolframAlpha. URL: https://www.wolframalpha.com/examples/Math.html (дата обращения: 28.01.2017).
- Set Command Window output display format // MathWorks. URL: https://www.mathworks.com/help/matlab/ref/format.html (дата обращения: 29.01.2017).







