Задача:
Исследовать асимптотическими методами решение с начальными данными 
, 
. Привести соответствующий численный счет при малом значении 
, сравнить полученное асимптотическое решение с численным решением.
Решение:
Дано уравнение:
Разложим искомую функцию u в ряд по степеням 
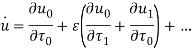
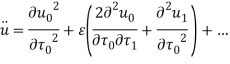
Сгруппируем слагаемые по степеням :
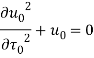
Решением получившегося уравнения с начальными условиями , является функция 
гармонического осциллятора, которую запишем в виде:
, где 
- время.
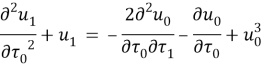
Правая часть:
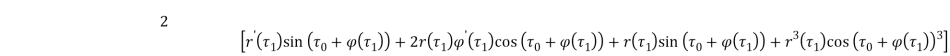
Обозначим: 
Упростим правую часть:
Для того чтобы не происходил резонанс, необходимо исключить члены 
и 
той же частоты, что и гармонический осциллятор.
Получаем систему:
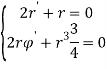
Решаем дифференциальные уравнения:
Итак, выпишем итоговый результат:
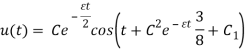
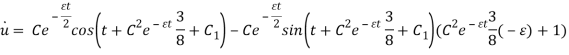
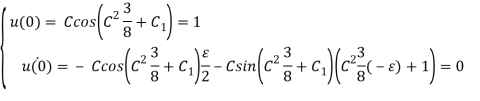
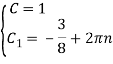
Ответ:
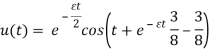
Фазовый портрет
Для построения фазового портрета используем пакет MatLab для численного решения обыкновенных дифференциальных уравнений.
Приводим наше уравнение к системе:
Пишем вспомогательную функцию для ode45:
function f=system(t,y)
eps = 0.3;
f=[y(2); -y(1) - eps*(y(2) - (y(1))^3)];
end
Cкрипт Матлаба, строящий фазовый портрет:
clear;
eps=0.1;
grid on
hold on
options = odeset('RelTol',10e-10);
xrange=5;
yrange=5;
step=1;
xx=-xrange:step:xrange;
yy=-yrange:step:yrange;
for i=1:length(xx)
for j=1:length(yy)
[T,Y]=ode45(@system,[0 50],[xx(i) yy(j)],options);
hLine2=plot(Y(:,1),Y(:,2),'b-')
end
end
axis([-xrange xrange -yrange yrange])
xlabel('U')
ylabel('V')
title(['Фазовый портрет при \epsilon =',num2str(eps)])
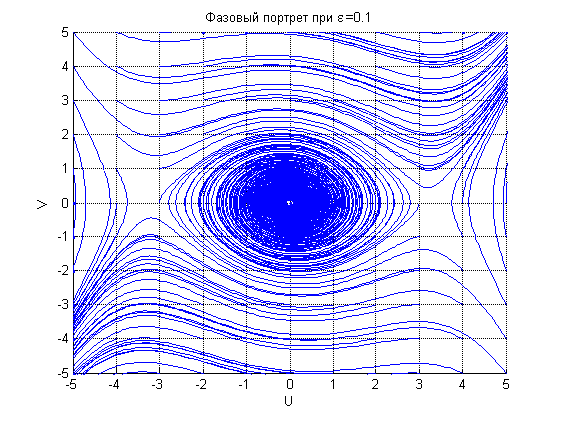
Решение 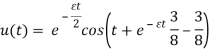при 
сходится к нулю.
Графики решений:
[t,y]=ode45(@system,[0 100],[1,0]);
plot(t,y(:,1),'r-');
grid on
hold on
C=1;
C1 =-3/8;
u=(C.*exp(-eps.*t./2).*(cos(t+(C^2).*exp(-eps.*t).*3/8+C1)));
plot(t,u);
xlabel('t');
ylabel('U');
title(['Численное и аналитическое решения при \epsilon = ',num2str(eps)]);
legend('Численное','Аналитическое');
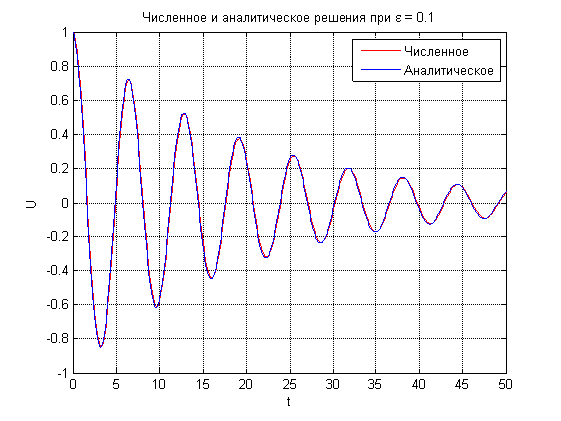
Численное и аналитическое решения практически совпадают. Вывод — поставленная задача решена.
Литература:
- Зорич В. А. Математический анализ М.: ФАЗИС; Наука; Ч.I. — 1997, 568с.; Ч.II. — 1984, 640с.
- Максименко В. Н., Меграбов А. Г., Павшок Л. В. Курс математического анализа: учебное пособие Ч.I. — 2009, 345с.;
- Гандер В., Гржебичек И. Решение задач в научных вычислениях с применением Maple и MATLAB. ISBN: 985–6642–06-X. Издательство «Вассамедина» 2005г. 520 с.
