Хорошо известно, что через две заданные точки проходит единственная прямая. Тогда вопрос, через три заданные точки, какая единственная кривая плоскости может проходить, очень логичен. Нарисовать таких кривых можно очень много, но чтобы эти кривые имели вполне определенную формулу задания и, к тому же были гладкими кривыми, уже заставляет задуматься. Рассмотрим задачи такого типа среди известных элементарных кривых.
Требуется через три заданные точки построить окружность и найти ее уравнение, но затем через эти же три точки построить параболу и опять найти ее уравнение, и возникает вопрос, какие еще можно провести кривые, которые можно задать аналитически. Эти задачи находятся на стыке теорий аналитической геометрии, линейной алгебры и математического анализа.
И именно такие различные способы решения одной исходной задачи наиболее интересны. Но эта задача имеет логическое продолжение. Если взять четыре точки на плоскости, то тогда про какие кривые можно говорить. Здесь таких кривых уже на порядок меньше. Очевидно, это будет график функции, определяемый кубическим многочленом и это может быть сплайн.
Использование общего вида уравнения окружности 
может помогать решению задач более сложного вида с двумя параметрами, что отражено в последней задаче.
Задача1. Даны вершины треугольника ABC. Найти уравнение окружности, описанной около треугольника ABC, если A(2;4), B(4;2), C(8;6) и построить данную окружность.
Каждая из точек A, B и C лежит на окружности, т. е. координаты каждой из этих точек удовлетворяет уравнению окружности . Для нахождения a, b и r напишем три равенства, подставив в последнее уравнение координаты точек A, B и C:
;
;
.
Исключая r2, приходим к системе уравнений
или 
Отсюда 
; 
. Значит, 
находим из уравнения . Итак, искомое уравнение окружности записывается в виде 
.
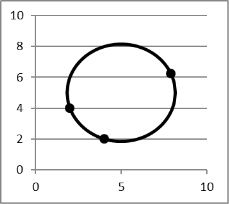
Рис. 1. График окружности
Задача2. Найти уравнение параболы и построить параболу, проходящую через те же три точки A(2;4), B(4;2), C(8;6).
Уравнение параболы 
. Запишем систему, используя координаты точек
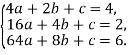
Вычитая из второго уравнения первое получаем зависимость 
. Затем вычтем из третьего уравнения второе и заменим b. Получили 
, 
, 
. Таким образом, уравнение параболы принимает вид 
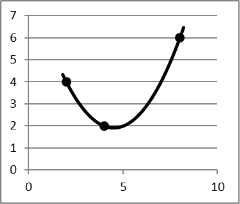
Рис. 2. График параболы .
Задача 3. Найти уравнение и построить кривую, проходящую через заданные четыре точки.
Рассмотрим пример построения сплайна второй степени дефекта 1, т. е. гладко склеенных двух парабол. Даны три точки А1(1;2), А2(2;1), А3(3;2), через которые проходит парабола S1, точка склейки В0(4;5), и точка А4 (6;5), через которую проходит парабола S2.
Построим сплайн:
,
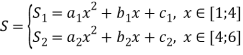запишем все условия в систему:
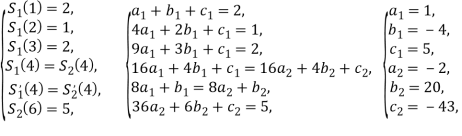
Таким образом, уравнение сплайна имеет вид:
.
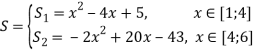При этом очевидно, что точка склейки имеет вспомогательный характер при построении данной кривой.
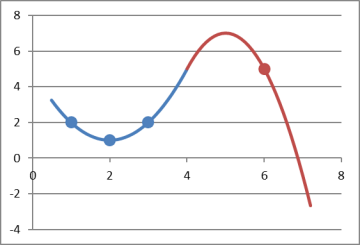
Рис. График сплайна S.
Задача 4. Найти все значения параметров a и b, при которых заданная система уравнений
имеет два решения 
, 
, координаты которых удовлетворяют условию
Рассмотрим решение. Перепишем условие:
или 
,
значит оба решения лежат на окружности с центром в точке О(0;0). Рассмотрим теперь первое уравнение системы
.
Это есть уравнение окружности с центром в точке О1(1;-2) и радиусом 
Рассмотрим теперь второе уравнение системы
Это есть уравнение окружности с центром в точке О2(
-6;) и радиусом 3.
Мы получили, что точки 
, 
одновременно лежат на трех окружностях, одна из которых с центром в точке О(0;0):
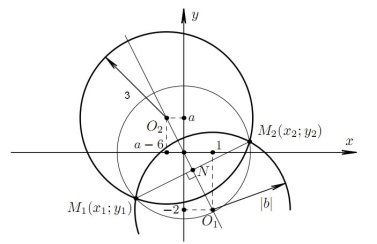
Рассмотрим сначала окружности с центрами О1(1;-2) и О(0;0). Отрезок
будет перпендикулярен ОО1, так как окружности пересекаются в точках 
и 
. Точку пересечения и ОО1 обозначим N. Теперь рассмотрим окружности с центрами О2(-6;) и О(0;0). Аналогичным способом получаем, что точки О, О1, О2 лежат на одной прямой, проходящей через точку N.
Уравнение прямой, проходящей через точки A(a1;a2), B(b1;b2), имеет вид
Подставим значения точек О1 и О2:
Подставим в полученное уравнение координаты точки О, так как эта точка также принадлежит данной прямой
Итак,
.
Рассмотрим теперь свойство двух пересекающихся в двух точках окружностей с радиусами r1 и r2, где d — отрезок, соединяющий центры этих окружностей:
Подставим значения нашей задачи
Получили ответ: 
.
Задачи такого типа позволяют изучать новые свойства уже хорошо известных кривых и дают возможность получать представления о таких замечательных кривых, как сплайны.
Оказывается, что сплайны [1] имеют особое прикладное значение, например в механике они задают деформацию гибкой пластины или стержня, зафиксированных в отдельных точках. Особое преимущество сплайнов, что их можно построить проходящими через любой конечный набор точек и они всегда являются гладкими кривыми (без точек излома).
Литература:
- Покорная, И. Ю. Сплайны как основа моделирования / И. Ю. Покорная, И. В. Плоткина // Некоторые вопросы анализа, алгебры, геометрии и математического образования: материалы Международной научно-методической конференции кафедры высшей математики. — Воронеж: Издательско-полиграфический центр «Научная книга», 2016. — № 4. — С. 158–160.
