In this paper we obtained a formula for the general solution for one class of Riccati equation. This formula was tested on the known results. The existence theorem of solution of Cauchy problem is proved.
Key words: Riccati equation, the general solution, the Cauchy problem
The Riccati equation is one of the most interesting nonlinear differential equations of the first order, which is used in algebraic geometry, calculus of variations, control theory, theory of conformal mappings, quantum field theory [2], financial mathematics [1], etc.
It is known that the solutions of Riccati equation are not generally obtainable by integration. Apart from the general Riccati equation, there are many special cases of the Riccati equation with coefficients of a certain kind. Many of these special cases have integrable solutions [3, 6, 4, 5].
In this paper we investigate the Riccati equation with coefficients that define a class of Riccati equations.
Solution of aclass of Riccati equation.
We consider the general Riccati equation:
![]() (1)
(1)
where a(t), b(t) and c(t) are known continuous functions on I =(t1, t2), t1 < t2.
Theorem 1. Let the following conditions are fulfilled
![]() (2)
(2)
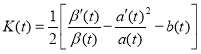 (3)
(3)
where K′(t), β′(t), a′(t) ∈C(I), a(t)≠0, β(t)≠0 for all t(t1, t2). Then the function given by the formula:
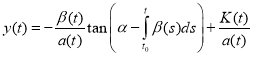 (4)
(4)
where α is arbitrary constant and 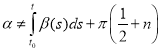 , t0(t1, t2) is the general solution of equation (1).
, t0(t1, t2) is the general solution of equation (1).
Proof. To verify the validity of the formula (4), we show that it satisfies the equation (1). We find the derivative
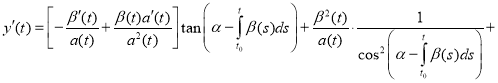
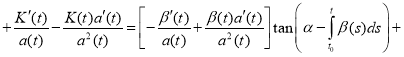
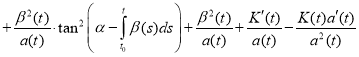 (5)
(5)
and we substitute (4) and (5) in equation (1):
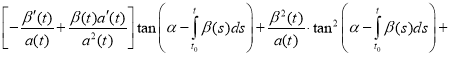
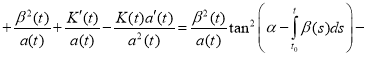
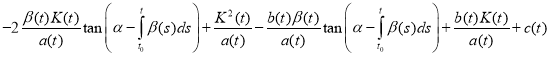 .
.
Combining like terms, we get
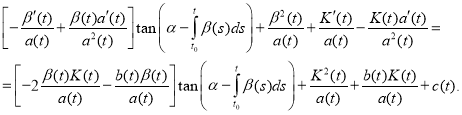 (6)
(6)
Obviously, that the equation (6) takes place when the next equalities are hold:
![]() (7)
(7)
![]() (8)
(8)
Equality (7) can be verified by substituting in this equation the function:
![]() (9)
(9)
which expressed from the condition (3):
![]() ,
,
i.e.
![]() .
.
To verify (8), we multiply it by a(t) and using condition (2) we obtain
![]() .
.
Using the condition (3) and the equality (9) we have
![]() ,
,
therefore:
![]() ,
,
which proves the equality (8). Thus we have proved Theorem 1.
Solution of the Cauchy problem for aclass of Riccati equations.
Consider the Cauchy problem for the Riccati equation (1) with initial condition
![]() (10)
(10)
where ![]() , t0(t1, t2).
, t0(t1, t2).
Theorem 2. Let the conditions of the Theorem 1 are hold and
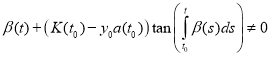
for all t(t1, t2). Then a solution of the Cauchy problem (1), (10) exists and given by
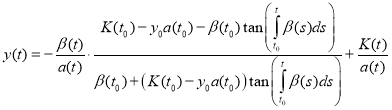 (11)
(11)
Proof. To prove the theorem we find the derivative of the function y(t):
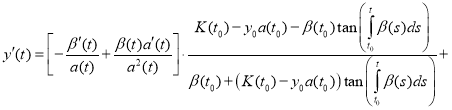
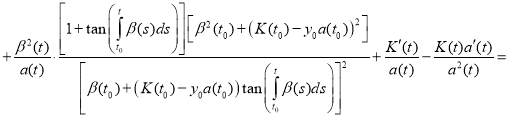
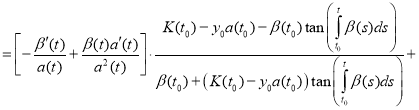
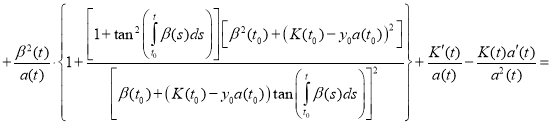
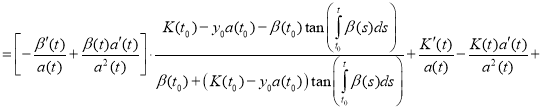
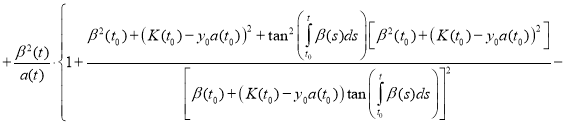
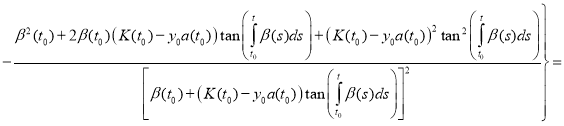
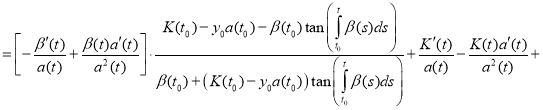
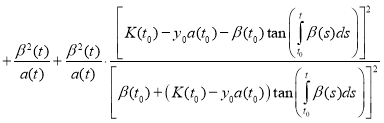 (12)
(12)
Substitute (11) and (12) in equation (1):
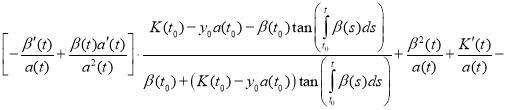
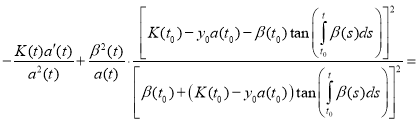
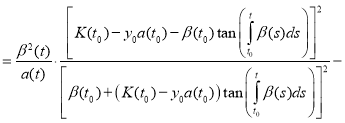
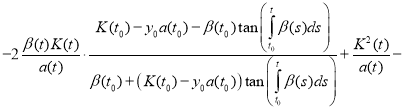
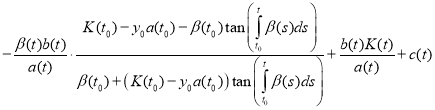 .
.
Combining like terms, we get
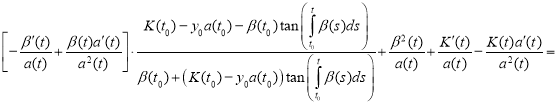
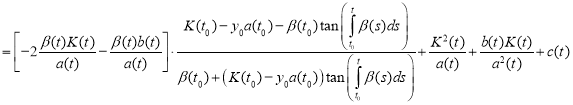 .
.
This equality will take place when the equalities (7) and (8), the validity of which are proved in Theorem 1, hold.
Thus Theorem 2 is proved.
Comparison with known results.
In Kovalevskaya paper [4] the Riccati equation (1) has been investigated in the case when functions c(t), a(t) are arbitrary functions and the function b(t) has been expressed through them:
![]() (13)
(13)
In this case a formula for the solution of the equation (1) has the form [4]
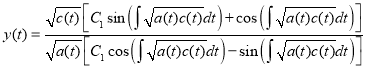 (14)
(14)
where C1 is constant.
First, we show that the condition (13) follows from (2) and (3) with K(t) = 0. Indeed, if K(t) = 0 then the conditions (2) and (3) will take the forms
![]() (15)
(15)
![]() (16)
(16)
From (15) we find
![]() (17)
(17)
which substituted in (16) gives
![]() .
.
We have got the condition (13).
Secondly, we show that the formulas (4) and (14) are equivalent if the conditions (2), (3), (13) are fulfilled with ![]() . Taking into account (17) the formula (14) can be written as follows
. Taking into account (17) the formula (14) can be written as follows
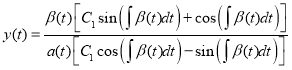 .
.
Further transforming as follows:
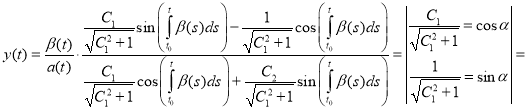
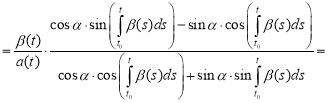
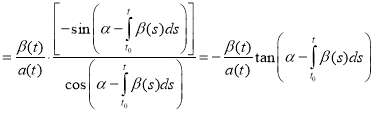 ,
,
we get the formula (4) for the solution of the Riccati equation. Thus, well-known result [4] is a special case of the result obtained above in p.2.
In [7] was considered the Riccati equation of the form
![]() (18)
(18)
and was shown that under the conditions
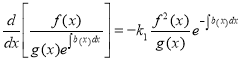 , k1-const, k1≠0(19)
, k1-const, k1≠0(19)
![]() , k2 — const, k2 ≠0, (20)
, k2 — const, k2 ≠0, (20)
the Riccati equation (18) is integrable and its general solution is given by the formula
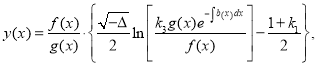 (21)
(21)
where k3 is arbitrary constant and Δ=(1+k1)2–4k2<0.
Comparison of the results of [7] and paragraph 2 this paper shows that the conditions (19) and (20) are special cases of conditions (2), (3) and the formula (21) is a special case of formula (4) with ![]() and
and ![]() .
.
Examples.
We solve the following Riccati equations given in [3] using the formula (4).
-
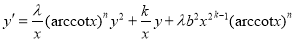 . With
. With 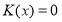 ,
, 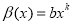 the conditions (2) and (3) are hold and from (4) we get the solution
the conditions (2) and (3) are hold and from (4) we get the solution
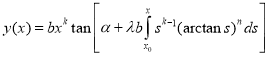 .
.
-
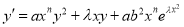 . With
. With 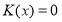 ,
, 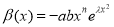 we have
we have
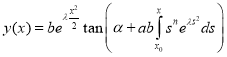 .
.
-
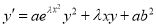 . With
. With 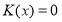 ,
, 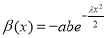 we have
we have
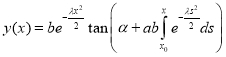 .
.
-
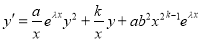 . With
. With 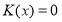 ,
, 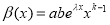 we have
we have
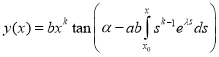 .
.
-
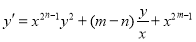 . With
. With 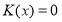 ,
, 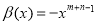 we have
we have
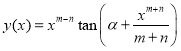 .
.
-
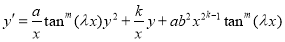 . With
. With 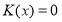 ,
, 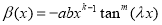 we have
we have
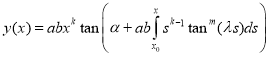 .
.
-
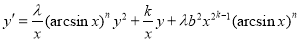 . With
. With 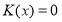 ,
, 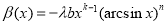 we have
we have
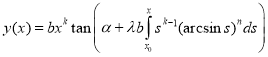 .
.
-
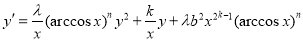 . With
. With 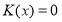 ,
, 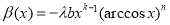 we have
we have
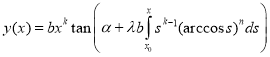 .
.
-
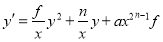 . With
. With 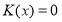 ,
, 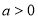 ,
, 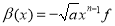 we have
we have
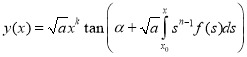 ;
;
with ![]() ,
, ![]() ,
, ![]() we have
we have
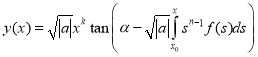 .
.
-
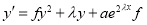 . With
. With 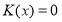 ,
, 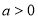 ,
, 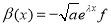 we have
we have
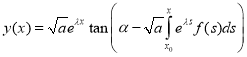 ;
;
with ![]() ,
, ![]() ,
, ![]() we have
we have
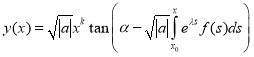 .
.
-
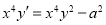 . With
. With 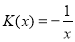 ,
, 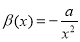 we have
we have
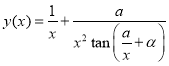 .
.
-
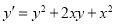 . With
. With 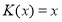 ,
, 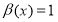 we have
we have
![]() .
.
The received solutions of these equations coincide with the solutions referred in [1].
Conclusion.
The formula of the general solution of the Riccati equation is presented. The formula is obtained by certain relations among the coefficients a(t), b(t) and c(t), in the form of some differential expressions, involving some arbitrary functions. The formula for the solution of the Cauchy problem for certain class of Riccati equation is also presented.
References:
- Boyle P. P., Tian W. and Guan F. The Riccati Equation in Mathematical Finance // J. Symbolic Computation, 2002, 33, pp. 343–355.
- Egorov A. I. Riccati equations, Nauka, Moscow, 2001.
- Kamke E. Differentialgleichungen: Losungsmethoden und Losungen, I, Gewohnliche Differentialgleichungen, B. G. Teubner, Leipzig, 1977.
- Kovalevskaya N. M. On some cases of integrability of a general Riccati equation, ArXiv: math., CA/0 604243v1, 2006.
- Matveev N. M. Methods of Integration of Ordinary Differential Equations, Vysshaya Shkola, Moscow, 1967.
- Polyanin A. D., Zaytsev V. F. Handbook of Exact Solutions for Ordinary Differential Equations, CRC Press, Boca Raton, New York, 2003.
- Tiberiu Harko, Francisco S. N. Lobo and Mak M. K. A Chiellini Type Integrability Condition for the Generalized First Kind Abel Differential Equation // Universal Journal of Applied Mathematics, 1(2), 2013, pp. 101–104.







