О динамике создания художественных произведений И. К. Айвазовским



На основе анализа творческой среды, возникшей вокруг художника И. К. Айвазовского, предлагается математическая модель лидера в субкультуре. Модель представлена начально-краевой задачей для системы двух дифференциальных уравнений в частных производных.

Ключевые слова: субкультура, живопись, математическое моделирование, дифференциальные уравнения, численные методы

К 200-летию И. К. Айвазовского

Введение. Во все времена в обществе возникали различные социальные группы и субкультуры [13–15, 19, 32, 38, 39] со своими ценностями, идеологической и материальной составляющими, лидерами. На сегодняшний день для прогнозирования их эволюции и оценки их роли в обществе разрабатываются математические модели. Значительная часть моделей основывается на работах специалистов, пытающихся объяснить причины возникновения социальных групп, их внутренние связи, их эволюцию [22, 23, 46–51]. Процесс построения моделей социальных систем, в отличие от моделей взаимодействующих популяций [3, 12, 27, 28], в силу сложности формализации происходящих в них процессов, происходит медленно. Часть математических моделей разрабатывается без учета реальных процессов, происходящих в самоорганизующихся социальных системах [4, 36, 44], некоторые строятся без учета реальных статистических данных. Тем не менее, некоторые модели, как показано в [7, 24–26, 30 31, 37, 40, 41, 42, 45], разработанные на основе немногочисленных количественных показателей, достаточно хорошо описывают самоорганизацию творческих субкультур. Значительно сложнее описать эволюцию лидера творческой субкультуры.

В работе на основе анализа творческой среды, возникшей вокруг художника И. К. Айвазовского, дается обоснование модели лидера творческой субкультуры. Творческая среда представлена различными субкультурами такими, как субкультуры художников, писателей, ученых, а также их материальными носителями такими, как музейные экспонаты, природные ландшафты, архитектурные сооружениями.

Процесс становления художников, произведения которых со временем получают широкое признание, очень сложный. У каждого из них свой творческий путь, но есть и то, что характерно для большинства из них. Общим является их творческое взаимодействие не только внутри самой субкультуры и с представителями других субкультур, но и со всеми слоями общества. Число и значимость создаваемых ими произведений зависят не только от личных качеств художника, но и от широты их контактов внутри общества [26, 42].

В работе использовались биографические данные И. К. Айвазовского, изложенные в [1, 6, 8–11, 20–22, 34, 43].

Художник Иван Константинович Айвазовский (1817–1900)внес неоценимый вклад в мировую культуру XIX века. Он родился в обыкновенной купеческой семье, проживавшей в Крыму в городе Феодосия, далеком от центров художественной жизни. Талант будущего художника-мариниста зародился и развивался в процессе наблюдения за водами заливов Черного моря. Впечатления, полученные художником в процессе наблюдения за стихией, накапливались ежедневно и, впоследствии, вылились в сюжеты будущих картин. Способности Айвазовского были замечены учителями гимназии, архитектором города, которые оказывали ему небольшую материальную поддержку в увлечении живописью. В возрасте 16 лет Айвазовский поступает в Петербургскую Академию Художеств, где впервые получает возможность окунуться в творческую обстановку. В период обучения Айвазовский знакомится с известными художниками (Воробьев М. Н., Таннер Ф., Штеренберг В. И.), писателями и поэтами (Крылов И. А., Жуковский В. А.), меценатами (Томилов А. Р., Казначеев А. И.). Благодаря своим успехам художник оканчивает Академию на 2 года раньше положенного срока и уже в 1838 году возвращается в Крым — начинается первый этап его самостоятельного творчества.

Двухлетний творческий период пребывания в Крыму сопровождался расширением круга знакомств художника. В первом плавании по Черному морю происходит знакомство с будущими яркими флотоводцами Корниловым В. А., Нахимовым П. С., Лазаревым М. П., Панфиловым А. И. Участвуя в военных операциях генерала Раевского Н. Н. на Кавказском побережье Айвазовский знакомится с ссыльными декабристами Одоевским Н. Н., Лерером Н. И., Нарышкиным М. М. По мотивам морских и сухопутных экспедиций создаются произведения живописи. Вместе с мастерством художника растет и его известность в России.

Европейские школы живописи стали возникать еще в XII веке сначала в Италии (флорентийская, венецианская и др. [21]), а затем и в других странах Европы. К началу XIX века Европа накопила значительное число произведений живописи, находящихся в частных коллекциях, художественных галереях и музеях. На рис. 1 отражено изменение числа наиболее известных художников стран Европы с XII по XVIII век, внесших вклад в мировую живопись (число художников за XVII век принято равным единице), а на рис. 2 — распределение числа (в долях) произведений художников по шести странам Европы, созданных к началу XIX века.

В отличие от Европы отход от церковной живописи, господствующей много веков в России, началась в конце XVII века. К середине XVIII века выросла большая группа российских художников, объединенная Академией художеств. Начинается подготовка молодых российских живописцев сначала в стенах Академии, а затем в Италии и других странах Европы. В 1840 году для совершенствования в искусстве пейзажной живописи в пенсионерскую поездку в Италию отправляется и Айвазовский.

Айвазовский в течение четырех лет изучает работы старых мастеров сначала в Италии, а затем Голландии, Франции, Англии, Испании, Португалии. В Италии, изучая живопись, организует творческое объединение художников (художники Иванов А. А., и Тернер Д., гравер Иордан Ф. И.). Знакомится с писателями и общественными деятелями (Гоголь Н. В., папа Пий XVI).

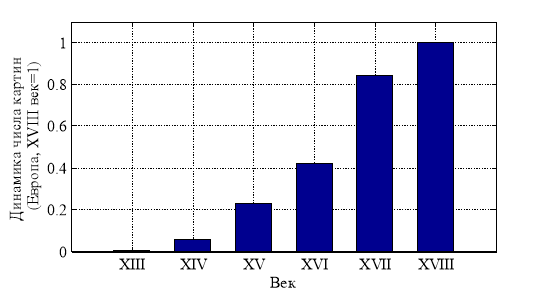
Рис. 1.

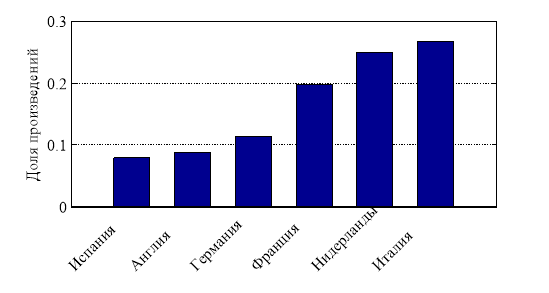
Рис. 2.

В 1844 году Айвазовский возвращается в Россию, сначала в Петербург, а затем в Феодосию, в которой он и прожил большую часть своей жизни. Однако, интенсивная творческая работа на берегах Черного моря совмещается с постоянными поездками в различные города России и Европы. Айвазовский также неоднократно посещает Египет, Америку, Турцию, участвует в археологических раскопках и в морских научных экспедициях, работает в осажденном Севастополе в 1854 году, присутствует в театре военных действий русско-турецкой войны 1877–1878 годов. Постепенно в круг его друзей входят известные писатели, поэты и композиторы (Белинский В. Г., Майков А. В., Фет А. А., Чехов А. П., Глинка М. И., Серов А. Н.), ученые, мореплаватели и путешественники (Литке Ф. П., Чихачев П. А., Мечников И. И.). Поддержку художнику оказывают не только известные российские (Томилов А. Р., Суворин А. С., Третьяков П. М.) и зарубежные (турецкий султан Абдул-Азиз, папа Пий XVI) меценаты, но и Российские Императоры (Николай I, Александр I, Александр II). Весь его творческий путь вплоть до 1900 года сопровождался многочисленными контактами с представителями творческих субкультур, в общении с которыми рождались новые образы, воплощенные впоследствии в его работах. Всего в различных источниках цитируются более 3000 контактов Айвазовского с представителями различных творческих и социальных групп. Поклонники его творчества оказывали ему материальную поддержку, что, в свою очередь, благоприятно сказывалось на скорости реализации возникающих образов. Им создано около 6000 произведений живописи, а при поддержке меценатов организовано более 120 выставок в различных городах России, Европы, Америки.

Айвазовский в Феодосии создал свою мастерскую, в которой работали ставшими впоследствии известными художниками Куинжди А. И., Сахаров А. А., Лагорио Л. Ф., основал художественную галерею. Из всех русских художников и европейских художников маринистов создал наибольшее число произведений.

Математическая модель. В качестве основной характеристики, описывающей динамику числа накопленных образов художником, берется количество созданных произведений. Альтернативной характеристикой может быть площадь полотен, на которых реализованы различные сюжеты. Как следует из анализа статистических данных, эти характеристики практически совпадают.

Пусть – число собственных образов, которые художник может реализовать за все время своего творчества, не используя при этом накопленную информацию с представителями различных социальных групп, а – число образов, которые он уже реализовал в своих произведениях. Тогда скорость изменения числа образов должна быть пропорциональна числу образов, которые он уже реализовал в своих произведениях, и доле тех образов, которые он еще может реализовать из оставшихся у него образов. Тогда скорость изменения числа образов описывается уравнением [26, 33]

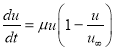,(1)

где — константа.

Накопление информационного ресурса, необходимого для создания новых полотен, происходит в условия контакта с представителями различных социальных групп, интересующихся как произведениями художника, так и его творчеством. Одновременно с информационной поддержкой от творческих субкультур художник получал и материальную поддержку от субкультуры меценатов. В модели принимается, что первая поддержка увеличивает количество образов, а вторая — увеличивает скорость их реализации.

У Айвазовского процесс накопления информационных и материальных ресурсов происходил во время многочисленных поездок по территории России, стран Европы, Азии и Америки. На рис. 3 отражена динамика поездок по городам России, Европы, Америки и Азии с 1834 по 1896 гг. Общее количество поездок принято равным единице. Учтено 99 поездок. Часть созданных им произведений осталась в местах его пребывания. Из более чем 120 прижизненных выставок картин Айвазовского около половины были организованы за границами страны и часть выставленных произведений была приобретена любителями живописи (по нашим оценкам не менее 1000). На территории России в начале XX века не менее чем 300 частных лиц и музеев приобрели произведения художника. То есть поездки художника по странам сопровождалось не только рождением новых образов, но и распространением его произведений. Скорость увеличения числа поездок от времени с 1834 по 1850 гг. описывается логистической зависимостью, а с 1850 по 1896 гг. она практически постоянна (рис. 3).

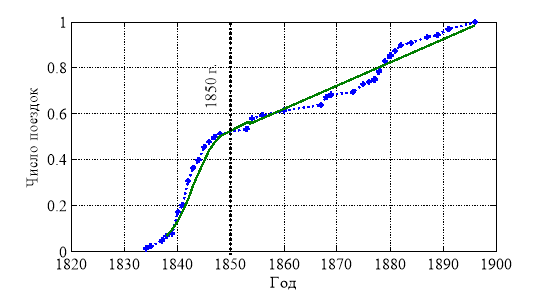
Рис. 3.

Примем, что траектория творческого движения художника представляет собой отрезок единичный длины, на котором расположены информационные ресурсы, представляющие собой объекты природы, художественные галереи, библиотеки, выставки, информационные ресурсы творческих групп и меценатов [1, 8, 10, 20, 21, 29, 34]. Во время движения в информационном пространстве художник собирает новые образы и одновременно часть из них воплощает в произведения. Время движения в информационном пространстве заканчивается с окончанием творческого периода.

Пусть — число образов на единицу длины, которые возникают у художника во время его движения в информационном пространстве, а — максимальное число образов на единицу длины, которые могут возникнуть. Информационное пространство все время пополняется, поскольку постоянно увеличивается число участников субкультуры вместе с новыми художественными произведениями. Примем, что рост ресурсов (образов) в материальном пространстве происходит по логистической зависимости с удельной скоростью роста равной . Движение художника в информационном пространстве происходит случайным образом.

Пусть во время движения в информационном пространстве у художника возникает обобщенных образов, которые могут быть воплощены в произведениях на текущий момент времени. Тогда максимальное количество образов увеличивается до . Поскольку в рассматриваемом информационном пространстве «находятся» и меценаты, то принимается, как и в моделях протокооперации [25, 26], что скорость роста числа произведений за счет поддержки меценатов увеличивается на , скорость убыли информации принимается равной , а ее старение происходит со скоростью .

Тогда математическая модель накопления информации и скорости ее реализации «движущимся в информационном пространстве случайным образом» художником, с учетом (1), примет вид

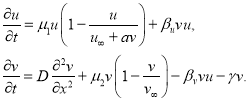(2)

Общее количество созданных произведений к моменту времени , подсчитывается по формуле

.

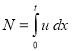В этих уравнениях , , , , — константы, характеризующие скорость накопления информации и скорость ее реализации, — параметр, характеризующий подвижность художника на «информационной территории».

К системе уравнений необходимо добавить граничные условия при и

и .(3)

Это обусловлено тем обстоятельством, что художник все время возвращался после поездок в одно и то же место (в модели это точка ), совершая тем самым поездки по замкнутым маршрутам.

В качестве начальных условий рассматриваются следующие условия:

при : ,,

где и малые положительные величины, а — дельта-функция Дирака.

При граничных условиях (3) нетривиальное стационарное решение системы уравнений (2) является решением системы уравнений

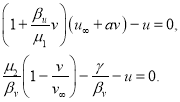(4)

Отсюда следует уравнение для

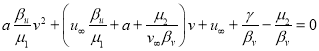.(5)

Это уравнение будет иметь положительный корень, если выполняется неравенство

.

Это неравенство будет выполняться при больших значениях и малых значениях (при активном накоплении информации и медленном ее старении). Значение положительного корня уравнения (5) тем больше, чем больше значение «совмещенного» параметра . Поскольку этот параметр не входит явно в первое уравнение в (4), то соответственно, в стационарном состоянии увеличивается и стационарное значение . То есть при прочих равных условиях функция будет расти тем быстрее, чем больше значение параметра и чем меньше значение параметра . Это в рамках рассматриваемой модели означает, что информация должна накапливаться быстрее, чем будет происходить ее исчерпание.

Система уравнений (2) при граничных условиях (3) имеет тривиальное стационарное решение

, .

Малые положительные возмущения этого положения равновесия

,

с точностью до величин второго порядка малости удовлетворяют, как это следует из (1), системе уравнений

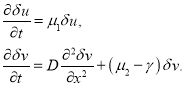
С учетом граничных условий (3) для и из первого уравнения следует, что будет возрастающей функцией времени. Функция будет возрастающей функцией времени, если будет выполняться неравенство . Тривиальное стационарное решение в этом случае будет устойчивым [2, 5, 16].

Зависимость как решение уравнений (4) при от совмещенного параметра при различных значениях и отражена на рис. 4. Из полученных результатов следует, что тем больше, чем больше значение совмещенного параметра (чем быстрее накапливается информация) и чем большая ее часть принимается для реализации (рис. 4 — , ).

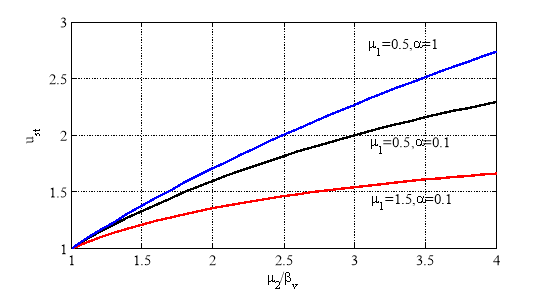
Рис. 4.

Решение нелинейных уравнений (2) при граничных условиях (3) решалось с применением конечно-разностных численных методов [17, 18]. На рис. 5 отражено изменение функции при значениях параметров , , , , , , , , . Символом * отражены статистические данные. Общее число учтенных в исследовании произведений, написанных Айвазовским (учтено около 1000 картин), принято равным единице.

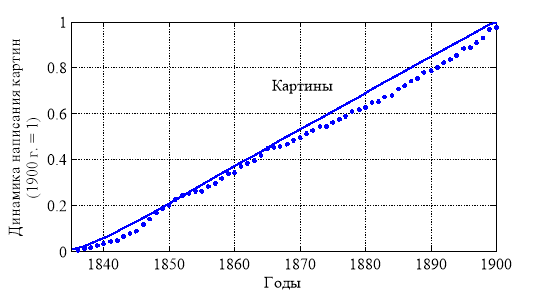
Рис. 5.

Заключение. Разработанная математическая модель с одной стороны не только учитывает основные особенности динамики накопления информации И. К. Айвазовским при его непрерывном физическом движении по территории Европы, но и достаточно хорошо описывает динамику создания им художественных произведений.

Литература:

1. 11 000 шедевров, 1000 мастеров классической живописи / Автор составитель И. Г. Мосин. — М.: Эксмо, 2007. — 1008 с.
2. Ekimov, A. V.Qualitative analyses of attainability set of nonlinear controllable systems // В книге: 20th International Workshop on Beam Dynamics and Optimization (BDO) IVESC-ICEE-ICCTPEA-BDO-2014. Edited by: D. A. Ovsyannikov. 2014. — С. 49.
3. Kolpak, E. P., Stolbovaya M. V., Frantsuzova I. S. Mathematical models of single population // Global Journal of Pure and Applied Mathematics. — 2016. — Т. 12. — № 4. — С. 2923–2934.
4. Shiryaev, D. V., Litvinenko I. L., Rubtsova N. V., Kolpak E. P., Blaginin V. A., Zakharova E. N. Economic clusters as a form of self-organization of the economic system // International Journal of Economics and Financial Issues. — 2016. — Т. 6. № S1. — С. 284–288.
5. Starkov, V. N., Stepenko N. A. Simulation of particle motion in the given speed fields // В сборнике: 2015 International Conference «Stability and Control Processes» in Memory of V. I. Zubov (SCP) 2015. С. 75–77.
6. Айвазовский. Документы и материалы. — Ереван: Айастан, 1967. — 405 с.
7. Андреев, В. В., Васильева Е. Б., Суконкина А. М. Попытка построения математических моделей для прогнозирования динамики социально-экономических систем // Вестник Чувашского университета. — 2006. — № 6. — С. 333–339.
8. Большая Российская Энциклопедия музеев, частных собраний и коллекций. — М.: РИПОЛ Классик, 2009. — 848 с.
9. Брасманов, Н. С. Иван Константинович Айвазовский. 1817–1900. — М.: Искусство, 1962. — 275 с.
10. Брасманов, Н. С., Брасманова С. А. Феодосийская картинная галерея имени И. К. Айвазовского. К 75-летию со дня основания. — Симферополь: Крымиздат, 1955. — 229 с.
11. Вагнер, Л. А., Григорович Н. С. И. К. Айвазовский. — М.: Искусство, 1970. — 269 с.
12. Горыня, Е. В., Колпак Е. П. Математические модели поиска экологической ниши // В сборнике: Устойчивость и процессы управления Материалы III международной конференции. — 2015. — С. 469–470.
13. Григорьева, Е. С. Толерантность и молодежные субкультуры // Вестник Воронежского института МВД России. — 2003. — № 1. — С. 19–22
14. Демидова, Д. А., Алферов Г. В., Колпак Е. П., Смирнова Т. Е. Нелинейный процесс взаимодействия между коррумпированной фирмой и отделом по борьбе с коррупцией // Проблемы механики и управления: Нелинейные динамические системы. — 2015. — № 47. — С. 17–31.
15. Духова, Л. И. Опыт построения модели субкультуры учителя // Мир образования — образование в мире. — 2006. — № 1. — С. 44–54.
16. Екимов, А. В. К вопросу об ограниченности интегральной воронки в билинейных управляемых системах // Системы управления и информационные технологии. — 2014. — Т. 56. — № 2.1. — С. 138–142.
17. Екимов, А. В., Жабко А. П., Смирнов Н. В. Матричный анализ эргодических полу марковских процессов // Вестник Санкт-Петербургского университета. Серия 10. Прикладная математика. Информатика. Процессы управления. — 2004. — № 1–2. — С. 16–29.
18. Жабко, А. П., Екимов А. В., Смирнов Н. В. Анализ асимптотики решения системы интегральных уравнений типа свертки с нормированным ядром // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2000. — № 1. — С. 27.
19. Жилкин, В. О понятии «информационная субкультура» // Высшее образование в России. — 2004. — № 10. — С. 152–153.
20. Каратыгин П. П. Иван Константинович Айвазовский и его XLII-летняя деятельность. 1836–1878. — СПб., тип. В. С. Балашова, 1878. — 94 с.
21. Картинные галереи Европы: собрание замечательнейших произведений живописи, ваяния зодчества, находящихся в Италии. — СПБ. Изд. М. Вольфа, 1878. — 278с.
22. Каталог 120-й выставки картин И. К. Айвазовского в залах Общества поощрения художников. — СПб., 1895.
23. Колесин, И. Д. Моделирование регуляции межэтнического восприятия // Психологический журнал. — 1997. — Т.18. — № 4.
24. Колпак, Е. П., Бронникова А. И., Полежаев В. Ю. Математическая модель стачечного движения в России в начале XX века // Молодой ученый. — 2015. — № 3 (83). — С. 4–15.
25. Колпак, Е. П., Габриелян Л А., Бронникова А. И., Крылова В. А. О математических моделях симбиоза // Молодой ученый. — 2015. — № 4 (84). — С. 6–14.
26. Колпак, Е. П., Гаврилова А. В. Математическая модель взаимодействия творческих субкультур // Молодой ученый. — 2016. — № 21. — С. 1–8.
27. Колпак, Е. П., Горыня Е. В. Математические модели «ухода» от конкуренции // Молодой ученый. — 2015. — № 11. — С. 59–70.
28. Колпак, Е. П., Горыня Е. В., Крылова В. А., Полежаев Д. Ю. Математическая модель конкуренции двух популяций на линейном ареале // Молодой ученый. — 2014. — № 12 (71). — С. 12–22.
29. Колпак, Е. П., Матвеева И. А. О библиотеках. Санкт-Петербург. 2004.
30. Колпак, Е. П., Селицкая Е. А., Габриелян Л. А. Математическая модель коррупции в системе «власть — общество» // Молодой ученый. — 2015. — № 10 (90). — С. 9–16.
31. Колпак Е. П., Скороходова Т. В. Математическая модель роста числа учащихся в средней и высшей школах России // В сборнике: Синергетика в естественных науках. Восьмые Курдюмовские чтения материалы Международной междисциплинарной научной конференции с элементами научной школы для молодежи. Ответственный редактор: Лапина Г. П. — 2012. — С. 274–275.
32. Колпак, Е. П., Французова И. С., Кувшинова К. В. Народное здравие в костромской губернии в конце XIX века // Приволжский научный вестник. — 2016. — № 2 (54). — С. 91–100.
33. Колпак, Е. П., Столбовая М. В. Математическая модель кинетики роста растений // Журнал научных публикаций аспирантов и докторантов. — 2013. — № 12 (90). — С. 230–232.
34. Коновалов, Э. Г. Словарь русских художников. — М. Эксмо, 2008. — 576с.
35. Крылова, В. А., Колпак Е. П., Сыромолотова К. И., Воротова Т. А. Математические модели формирования спортивных групп // Молодой ученый. — 2015. — № 8 (88). — С. 10–19.
36. Куижева, С. К. Уравнение Кортевега-де Фриза и математические модели в социально-экономических системах // Вестник Адыгейского государственного университета. Серия 4: Естественно-математические и технические науки. — 2015. — № 1 (154). — С. 20–26.
37. Леванский, В. А. Модели политических лидеров и президентские выборы в постсоветской России // Общественные науки и современность. — 2005. — № 5. — С. 74.
38. Масленченко, С. В. Анализ социальных ролей в субкультуре хакеров // Аналитика культурологии. — 2008. — № 10. — С. 246–255
39. Мацкевич, И. М. Криминальная субкультура // Российское право в Интернете. — 2005. — № 1. — С. 5.
40. Миндлин, Ю. Б., Колпак Е. П., Балыкина Ю. Е Проблемы использования кластеров в Российской Федерации // Вестник НГУЭУ. — 2014. — № 1. — С. 22–32.
41. Миндлин, Ю. Б., Колпак Е. П., Гасратова Н. А. Отличительные признаки кластеров и практика их применения в России // Политика и общество. — 2015. — № 5. — С. 666–675.
42. Плотинский, Ю. М. Математическое моделирование динамики социальных процессов. — M.: Изд-во МГУ, 1992. — 133 с.
43. Полунина, Н. М. Кто есть кто в коллекционировании старой России: Новый биографический словарю — М.: РИПОЛ КЛАССИК, 2003. — 560 с.
44. Разжевайкин В. Н. Лидер в диффузионной модели конкурентного типа // Журнал вычислительной математики и математической физики. — 2015. — Т. 55. — № 3. — С. 429
45. Смирнова, М. В., Колпак Е. П. Математическое моделирование снижения детской заболеваемости в России // В сборнике: Синергетика в общественных и естественных науках: Девятые Курдюмовские чтения Материалы Международной междисциплинарной научной конференции с элементами научной школы для молодежи. Ответственный редактор Лапина Г. П.. 2013. С. 222.
46. Старкова, Н. В. Возрастная структура населения и повозрастная интенсивность рождений как факторы изменения уровня рождаемости в Ленинградской области // Вестник Санкт-Петербургского университета. Серия 7. Геология. География. — 2008. — № 3. — С. 98–106.
47. Старкова, Н. В. Особенности демографического развития районов Ленинградской области // Вестник Санкт-Петербургского университета. Серия 7. Геология. География. — 2007. — № 4. — С. 87–97.
48. Старкова, Н. В. Особенности социально-экономического развития приграничных муниципальных районов ленинградской области // В сборнике: Стратегия развития приграничных территорий: традиции и инновации Материалы международной научно-практической конференции. 2014. — С. 350–359.
49. Старкова, Н. В. Современные особенности миграции населения Ленинградской области // В сборнике: Стратегия развития приграничных территорий: традиции и инновации Материалы II международной научно-практической конференции. 2015. — С. 173–180.
50. Старкова, Н. В. Тенденции и факторы миграции в странах Европы // В сборнике: География и геоэкология на службе науки и инновационного образования материалы XI Международной научно-практической конференции, посвященной Всемирному Дню Земли и 100-летию заповедной системы России. 2016. — С. 154–157.
51. Старкова, Н. В., Ложкинс А. Кластеризация стран Европы по демографическим признакам // Молодой ученый. — 2016. — № 9 (113). — С. 418–426.