Применение гидравлических приводов для формирования движения рабочих органов почвообрабатывающих машин ограничивается отсутствием силовых элементов, позволяющих работать в условиях значительного загрязнения, поэтому разработка рабочих органов, позволяющих формировать воздействие на почву, и не имеющих узлов, работающих в условиях внешнего трения, является актуальной задачей.
Для решения данной проблемы предложены конструкций рабочих органа почвообрабатывающих машин [1, 2, 3, 4] стойки которых выполнены в виде гибких трубчатых элементов, представляющих собой герметичные трубы некруглого поперечного сечения.
Напряженно-деформированное состояние и технические параметры гибкого трубчатого элемента зависят от следующих параметров: формы средней линии поперечного сечения; толщины стенки; радиуса центральной оси; величины центрального угла пружины; физико-механических характеристик материала. При проектировании гибких трубчатых элементов приходится иметь дело с задачей подбора геометрии сечения трубчатого элемента при условиях наложенных на остальные геометрические параметры, а так же на величины технических характеристик.
Гибкий трубчатый элемент проектируется для работы в заданном диапазоне давлений, от некоторого начального значения до некоторого предельного значения, при этом должно выполнятся условие прочности:
![]() (1)
(1)
Варианты элементов не удовлетворяющие данному условию должны быть исключены из рассмотрения.
При поиске варианта формы и размеров поперечного сечения необходимо предусмотреть возможность изготовления элемента из стандартной трубки-заготовки. Здесь для удобства контроля поперечных размеров трубки необходимо перейти от размеров, использующихся для теоретических расчетов, к размерам которые легко контролировать при изготовлении (см. рис. 1).
Величину диаметра пружины, либо радиус центральной оси необходимо выбирать исходя из компоновки рабочего органа.
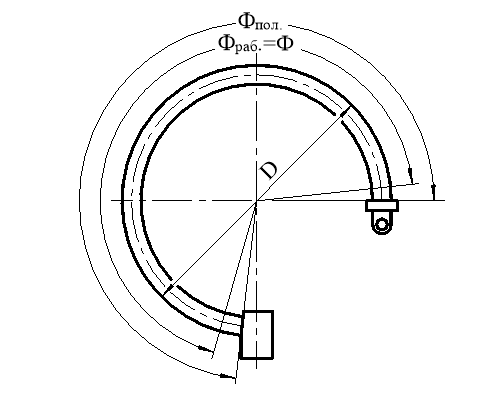
Рис. 1. Геометрические параметры проектируемых трубчатых элементов
При выборе значений центрального угла пружины необходимо учитывать нерабочие участки пружины у держателя и кончика. Следует различать рабочий центральный угол пружины Фраб. и полный центральный угол пружины Фпол. (см. рис. 1). Согласно экспериментальным данным Г. И. Тыжнова [5] величина рабочего центрального угла приближенно может быть определена по формуле:
![]() .
.
Величину свободного хода пружины λp необходимо выбирать из заданного интервала λp.min…λр.max:
![]() (2)
(2)
Рассмотрим подробно решение задачи выбора оптимального варианта конструкции гибкого трубчатого элемента.
Наилучшей конструкцией трубчатого элемента будет та, которая удовлетворяет одновременно двум критериям:
![]() (3)
(3)
![]() (4)
(4)
Где: k — вектор конструктивных характеристик проектируемой пружины; Mm — тяговый момент развиваемый трубчатым элементом; G — изгибная жесткость гибкого трубчатого элемента.
Таким образом, задача выбора оптимального варианта конструкции содержит неопределенность, так как необходимо выбрать вектор конструктивных характеристик k удовлетворяющий условиям (3), (4).
Для решения данной задачи рассмотрим широко используемую гипотезу, позволяющую свести многокритериальную задачу к однокритериальной [6]. Предположим, что решение системы однокритериальных задач (3), (4) найдено, при этом определены значения векторов kGkM, доставляющие максимальные значения соответственно критериям G(k), M(k):
![]() ,
, ![]() (5)
(5)
Совокупность величин ![]() , определяет в пространстве критериев некоторую точку, так называемую точку «абсолютного максимума». Тогда скалярная величина
, определяет в пространстве критериев некоторую точку, так называемую точку «абсолютного максимума». Тогда скалярная величина
![]() (6)
(6)
определяет в пространстве критериев некоторое расстояние от точки, соответствующей данному вектору k, до точки «абсолютного максимума». Иными словами выражение (6) определяет евклидово расстояние от точки (G(k), Mm(k)) до точки (![]() ,
, ![]() ) в пространстве критериев.
) в пространстве критериев.
Принимая в качестве нового критерия функцию (6) и определяя вектор k соответствующий условию:
![]() (7)
(7)
Находим конструкцию пружины с параметрами G, Mm. предельно близкими к точке «абсолютного максимума».
При фиксированном значении степени вытянутости сечения А/b решение задачи отыскания оптимального варианта конструкции с учетом условий (3), (4) упрощается. Это достигается, во-первых, за счет выбора формы поперечного сечения с оптимальными свойствами в плане изгибной жесткости, чувствительности, тяговой способности. Иными словами, при поиске вариантов форм сечения, которые могут быть изготовлены из трубок-заготовок диаметра d с различной толщиной стенки h при заданной степени вытянутости сечения А/b, необходимо рассматривать варианты сечений в определенном диапазоне значений В/В1, которые обеспечат, например, наибольшую изгибную жесткость. Во-вторых, при выборе вариантов конструкции из созданной базы данных трубчатых элементов с определенными свойствами, конструктор так же имеет возможность оптимизировать конструкцию в разных направлениях.
Таким образом, алгоритм проектирования гибких трубчатых элементов необходимо построить следующим образом:
- Для стандартной трубки-заготовки при известных значениях.h, d, А. подбираются возможные варианты геометрия сечения, то есть для заданной степени вытянутости сечения определяются все возможные варианты параметров А/В и B/B1. Графически указанная процедура показана на рис.2.
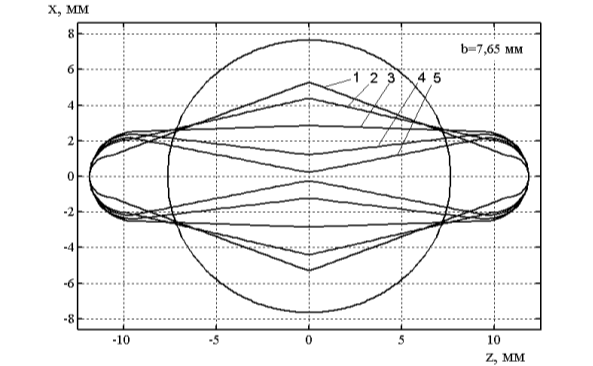
Рис. 2. Варианты геометрии сечения пружины при d=16 мм, А/b=1,4
- Из найденных вариантов геометрии трубчатого элемента при фиксированных значениях D, d, А., рном определить форму поперечного сечения, которая удовлетворяет условию прочности (см. рис. 3).
- Для найденного варианта трубчатого элемента, удовлетворяющего условию прочности, определить величину рабочего хода λр и проверить попадает ли найденное значение в интервал λр.min…λр.max.
- Рассматривая возможность изготовления трубчатых элементов из трубок-заготовок различного диаметра d и толщины стенки h, а так же меняя значения степени вытянутости сечения А/b, наружного диаметра D, рабочего центрального угла Фраб. в заданном диапазоне, необходимо создать базу данных трубчатых элементов на заданное давление с величиной рабочего хода в интервале от λр.min до λр.max, посредством многократного повторения вышеописанных операций.
- Из множества конструктивных решений выбрать оптимальный вариант.
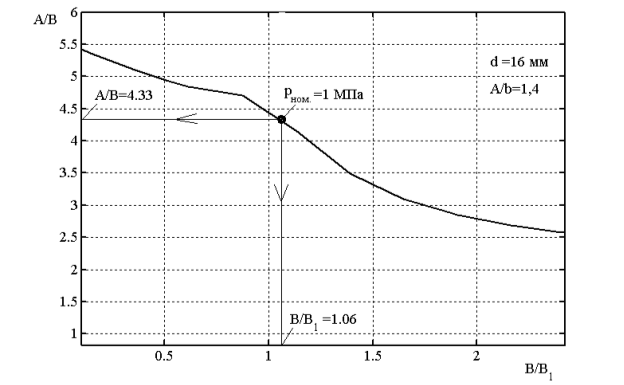
Рис. 3. Определение параметров сечения А/В и В/В1 удовлетворяющих условию прочности
Таким образом, предложен алгоритм, позволяющий подбирать геометрические размеры гибкого трубчатого элемента с учетом требований, предъявляемых к техническим параметрам рабочего органа почвообрабатывающей машины.
Литература:
- Устинов Н. Н. Математическая модель активного рабочего органа культиватора со стойкой в виде гибкого трубчатого элемента / Н. Н. Устинов, А. А. Маратканов, Н. И. Смолин // Современные проблемы науки и образования. — 2015. — № 1; URL: http://www.science-education.ru/121–17908 (дата обращения: 18.03.2015).
- Маратканов А. А. Экспериментальное определение характеристик активного рабочего органа культиватора со стойкой в виде гибкого трубчатого элемента / А. А. Маратканов, Н. Н. Устинов // Вестник Алтайского государственного аграрного университета. — 2015. — № 4(126). — С. 102-105.
- Устинов Н. Н. Рабочий орган культиватора / Сельский механизатор. — 2015. — № 12. — С. 30–31.
- Пат. 2009136304 А, Российская Федерация. МПК А01В 39/20, А01В 35/20. Рабочий орган культиватора [Текст] / Устинов Н. Н., Кокошин С. Н., Смолин Н. И. Заявители и патентообладатели: ФГОУ ВПО «Тюменская государственная сельскохозяйственная академия» (RU). — 2009136304/21; заявл. 30.09.2009; опубл. 20.09.2011. Бюл. № 14. — 3 c.:ил.
- Тыжнов Г. И. Деформации и напряжения в трубчатых манометрических пружинах. — Дис. канд. тех. наук: 01.02.06 / Томский ордена Трудового Красного Знамени политехнический институт имени С. М. Кирова. — Томск, 1964. — 185 с.
- Моисеев Н. Н. Математические задачи системного анализа. — М.: Наука, 1981. — 488 с.

