Определение энергетических и аэродинамических характеристик ротора Савониуса



В статье произведён анализ публикаций, касающихся исследования аэродинамических и энергетических характеристик ротора Савониуса. После проведённого анализа. Приведены основные достоинства и недостатки роторов данного типа.

Ключевые слова: ротор Савониуса, ветроэнергетическая установка.

Ротор Савониуса – это конструкция с лопастями, имеющими форму цилиндрических поверхностей. Основным достоинством данного ротора является возможность запускаться при минимальных скоростях ветра – от 3 м/с. Также к достоинствам относятся быстрый рост характеристик крутящего момента, конструкция надежна, низкая стоимость производства. К недостатку можно отнести малый коэффициент полезного преобразования воздушного потока, поэтому мощность данных устройств не превышает 4-6 киловатт. Наиболее часто ротор Савониуса используется в комбинированных устройствах, применяемых для разгона ветрогенераторов, построенных по схеме ротора Дарье.

В работе Даржании И. И. [9] проводятся исследования ротора Савониуса без нагрузки и с нагрузкой. Для холостого хода исследовались параметры авторотации ротора Савониуса. Под нагрузкой определялась электрическая мощность, снимаемая при помощи электрогенератора, соединенного с ВЭУ, а также проводились тензометрические измерения статических аэродинамических характеристик лопастей модели ВЭУ при различных фазах поворота относительно оси ротора и вектора скорости набегающего потока. Полученные в работе результаты имеют методическое и практическое значение, в частности, они будут важны для верификации разрабатываемых вычислительных моделей. В результате проведённых в работе экспериментов в аэродинамической трубе А-10 НИИ Механики МГУ, максимально достигнутый КПД равнялся 21%.

Сизов Д.А. в своей диссертации рассматривает [13] ветроэнергетические установки (ВЭУ) двух типов: с горизонтальной и с вертикальной осью вращения ротора. Для небольших хозяйств и бытовых нужд он рекомендует использовать вертикальноосевые установки, в частности, ВЭУ с ротором Савониуса, так как они имеют простую конструкцию, не требуют ориентации на ветер и обладают большим начальным моментом.

В работе Пьянкова К. С. и Топоркова М. Н. рассмотрено течение в двумерной постановке в рамках уравнений Навье-Стокса в роторах ветрогенераторов с вертикальной осью типа Дарье и Савониуса, а также их комбинации. Проведено параметрическое исследование характеристик ротора Дарье. Для всех конфигураций рассчитаны зависимости коэффициентов момента и мощности от параметра быстроходности ротора. Проведено исследование возможности автозапуска ротора Дарье из состояния покоя [10]. Метод, развитый в работе, обеспечивает безударное течение в местной сверхзвуковой зоне при небольшом уменьшении площади продольного сечения профиля и при практически неизменной подъемной силе. Данный метод расширяет идею использования «фиктивного» газа, применяемую ранее. Отличие заключается в способах возможности конструирования фиктивного газа, а также в численной реализации. Ранее расчет стационарного обтекания исходных профилей фиктивным газом производился в рамках потенциального приближения с использованием весьма специфических, развитых только для этого приближения численных процедур. В этой работе это делается в рамках процедуры установления, ставшей наиболее распространенным и простым в реализации методом расчета смешанных течений.

Рисунок 1 поясняет их на примере коррекции профиля NACA 6412, обтекаемого потоком с на угле атаки α = 2°. Исходный профиль обтекается с образованием скачка уплотнения (рисунок 1.а).

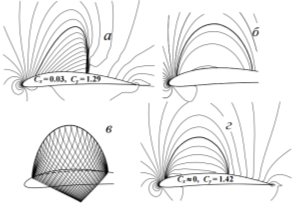
Рис.1

а – обтекание исходного профиля (NACA - 6412) совершенным газом; б – фиктивным газом: в – расчет сверхзвукового течения методом харакеристик от полученной в пункте б звуковой линии; г – обтекание модифицированного профиля совершенным газом

Коэффициенты волнового сопротивления и подъемной силы данного профиля и . На рисунке 1б отображена картина безударного обтекания того же профиля композитным газом. За пределами звуковой линии, где давление больше критического, соответствующего «звуковому» потоку, композитный газ тождественен «нормальному», например, совершенному газу. Во внутренней области нормальный газ заменяется “ненормальным”, то есть фиктивным, в котором при стационарном течении скорость потока не превышает скорость звука, вследствие этого невозможны ударные волны. На звуковой линии все термодинамические параметры, скорость звука, модуль скорости потока и число Маха совпадают в обоих газах.

На рисунке 1.в показано как методом характеристик решается соответствующая задача Коши, при этом используя в качестве изначальных данных полученные при обтекании композитным газом параметры на звуковой линии. Если течение без пересечений одноименных характеристик удается построить до «нулевой» линии тока, которая соединяет без изломов звуковые точки исходной образующей, то данная линия тока дает искомый участок контура суперкритического тела. В другом случае степень отличия фиктивного газа от нормального придется увеличить, что, может привести к большей степени отличия площади исходного и модифицированного контуров.

На рисунке 1.в при десятикратном уменьшении числа характеристик каждого семейства, нарисована характеристическая сетка, которая получается в процессе расчета сверхзвукового течения методом характеристик. На этом же рисунке сплошной кривой и штрихами отображены участки контуров исходного и суперкритического профилей. По сравнению с исходным площадь продольного сечения суперкритического профиля уменьшилась на 6.4%.

Рисунок 1.г дает найденное установлением поле чисел Маха, которое получается при обтекании суперкритического профиля нормальным, то есть совершенным газом. Для и α = 2° при нулевом волновом сопротивлении его [10].

В своей научной деятельности Редчица Д. А. [11] сформулирована постановка задачи динамики и аэродинамики роторов вертикально-осевых ветроустановок. Разработана математическая модель для расчета аэродинамических и энергетических характеристик ветроустановок на базе нестационарных осредненных по Рейнольдсу уравнений Навье-Стокса (URANS) несжимаемой жидкости. При анализе модели турбулентности использовалась однопараметрическая дифференциальная модель турбулентности SALSA. При нахождении оптимального решения системы исходных уравнений было получено с помощью неявного конечно-объемного численного алгоритма, который основан на методе искусственной сжимаемости и многооблачных вычислительных технологиях. Был детально рассмотрен анализ течения вокруг ротора Савониуса. Выделены основные стадии формирования вихревой структуры при вращении ротора. Стало известно влияние числа Рейнольдса и коэффициента быстроходности на энергетические характеристики ротора Савониуса.

Процессы аэродинамики ветроагрегата описываются определенными по Рейнольдсу уравнениями Навье-Стокса несжимаемой жидкости и выглядят следующим образом :

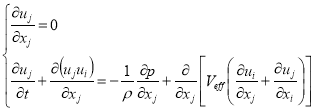(1)

где , =1,2 – декартовы координаты ; - время; - декартовы составляющие вектора скорости ; - давление, - плотность; - эффективный коэффициент кинематической вязкости; , - молекулярный и турбулентный коэффициенты кинематической вязкости.

При составлении модели турбулентности используется однопараметрическая дифференциальная модель турбулентности Spalart-Allmaras, адаптированная к тензору скоростей деформации (SALSA).

Система исходных уравнения (1) замкнутая дифференциальной моделью турбулентности, записывалась относительно произвольной криволинейной системы координат.Согласование полей давления и скорости осуществлялась с помощью метода искусственной сжимаемости, модифицированного для расчета нестационарных задач. Для создания дискретного аналога исходных уравнений вокруг ротора ВО ВЭУ в качестве базовых использовались регулярные сетки. В неодносвязных областях применялись многоблочные вычислительные технологии, в которых размерность отдельных пересекающихся сеток (блоков) не связана между собой. Такой подход дает нам право выработать единую методологию расчета течений вязкой жидкости вокруг роторов ВО ВЭУ сложной геометрической формы.

Данная система исходных уравнений интегрировалась численно с использованием метода контрольного объема. Для конвективных потоков использовалась противопоточная аппроксимация, основанная на схеме P.Roe третьего порядка точности. В моделях турбулентности для аппроксимации конвективных слагаемых применялась схема TVD с ограничителем потоков ISNAS третьего порядка. Производные в вязких членах аппроксимировались центрально-разностной схемой второго порядка.

Алгоритм решения уравнений основан на трехслойной неявной схеме с подытерациями по псевдовремени второго порядка точности по физическому времени.

В статье Горелова Д. Н. приведены результаты экспериментального исследования двухъярусного ротора Савониуса с оптимальным соотношением геометрических характеристик в гидроканале в условиях практического отсутствия влияния границ потока. Было обнаружено, что полезная мощность вырабатывается ротором в диапазоне изменения числа быстроходности от нуля до единицы, а максимальное значение коэффициента использования энергии потока достигает 20% [8].

Аскаровым Е. С. [6] была рассмотрена более простая модель ветровой энергетической установки с ротором Савониуса и неподвижной осью.

В статье Рожковой Л. Г. [12] рассмотрены основные критерии выбора типа, конструкции и размеров ветроколеса для вертикально-осевых ветроустановок с точки зрения его эффективности. Даны обоснованные рекомендации по выбору типа лопастей, их количества в ветроколесе, конструкции крепления лопастей, а также номинальной скорости ветра для расчета мощности ВУ.

В статье Джеффа Уолли, Мэтти Джонсона и Брайана Макмиллана [2] спроектирована модель ротора Савониуса и произведен ее анализ для определения турбулентных эксплуатационных свойств. Из предыдущих исследований был сделан вывод, что по сравнению с общей осью ветровых турбин в ламинарном потоке ротор Савониуса является более эффективен. Для создания имитации турбулентности использовались роторы различных ориентаций. При изменении ориентации были получены снижение затрат на производство электроэнергии от 20% до 55%.

В работе Роговски К. (Rogowski.K) и Маронски Р. (MaronskyR.) [4] при помощи вычислительной динамики и приложения ANSYSFluent проводится анализ двумерного ротора Савониуса. Для оценки аэродинамической силы используется динамика жидкости. Помимо этого, выполняется анализ различных результатов турбулентности. Полученные результаты сравниваются с результатами, полученными ранее в экспериментальной лаборатории Sandia National.

В работе SimondsM.H. и BodekA. [5] проводились эксперименты производительности ротора площадью 18 квадратных футов. Выходной вал был задан тормозным моментом, оказываемым ленточным тормозом. Частота вращения вала зависела от скорости ветра. Были получены интересные результаты, а именно: зависимость от крутящего момента, а также что при использовании ротора Савониуса система представляет собой практичный вариант ветряной мельницы, примерно в два раза эффективнее обычного вентилятора мельницы. При использовании для перекачивания воды, диаметр мембранного насоса должен быть выбран в соответствии с используемой общей насосной головки. Система лучше всего подходит для перекачивания, когда глубина скважины не превышает 20 футов. Дальнейшее усовершенствование ротора Савониуса должно выполнятся в двух направлениях. Первое - необходимо исследовать влияние изменений в форме лопастей ротора, и т.д., путем проведения исследований в аэродинамической трубе. Второе – нужно выбрать материалы в зависимости от конкретных условий.

В статье Джина Люка Менета (Jean-LucMenet) и Начида Бурабана (NachidaBourabaa) [1] говорится, что, хотя аэродинамические характеристики ветровых турбин Савониуса были достаточно исследованы, но по этим исследованиям получены разногласия, затрудняющие сравнение результатов. На основании данных исследований можно определить исходные параметры и доказать возможность улучшения аэродинамических параметров ротора Савониуса при помощи изменения геометрических размеров. В данном исследовании предлагается использовать ротор Савониуса с двумя лопастями и торцевыми пластинами. Высота ротора должна быть вдвое больше его диаметра. Отношение первичного перекрытие должно быть в пределах от 0,15 до 0,3 диаметра лопасти, тогда как отношение со вторичным перекрытием должно быть равно 0. Данное исследование применяется для численного моделирования потока. В результате моделирования получаются оптимальные геометрические размеры ротора. Результатом данного моделирования являются не только точные параметры потока, но и аэродинамическое поведение ротора. Результаты сравниваются с экспериментальными данными. В частности, возможно прогнозирование аэродинамических моментов для нескольких геометрических конфигураций. Влияние центрального вала изучаются на основании геометрических параметров внешнего шасси. Влияние числа Рейнольдса исследованы. Вышеперечисленное позволяет определить оптимальную геометрическую конфигурацию ротора.

Mahmoud N.H., EI-Haroun A.A., Wahba E. [3] изучали ветровые турбины Савониуса, имеющие различные геометрические параметры, для определения наиболее эффективных.

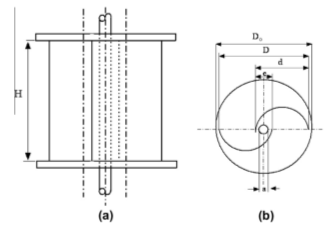
Рис.2. Схема одноступенчатого ротора Савониуса: a – вид сбоку; b – вид сверху

В результате было установлено, что ротор с двумя лопастями является более эффективный, чем ротор с тремя или четырьмя лопастями. Ротор с торцевыми пластинами более эффективен, чем без них. Двухступенчатые роторы более эффективны по сравнению с одноступенчатыми. Роторы, не имеющие коэффициента перекрытия, являются лучшими в эксплуатации по сравнению с имеющими данный коэффициент. Также было определено, что коэффициент мощности возрастает с ростом соотношения сторон.

На основании проведенного исследования работ этих авторов, можно представить основные аэродинамические и энергетические характеристики, принцип работы, а также основные достоинства и недостатки ротора Савониуса.

Генераторы на основе ротора Савониуса зарекомендовали себя с наилучшей стороны и имеют довольно широкое использование для качественного функционирования бытовых электростанций. По своей конструкции подобные роторы являются ветроколесами с несколькими полуцилиндрами, которые непрерывно вращаются вокруг своей оси. Плюсы такого ротора состоят в следующем: ветроколесо постоянно вращается в одну и ту же сторону и абсолютно не зависит от направления ветрового потока. Минусы же подобного ветрогенератора в низком коэффициенте использования энергии ветрового потока.

Литература:

1. Jean-Luc Menet, Nachida Bourabas Increase in the Savonius rotors efficiency via a parametric investigation [электронныйресурс] // http: //educypedia.karadimov.info/library/23_1400_jeanlucmenet_01.pdf (датаобращения 18.10.16)
2. Jeff Whalley, Matt Johnson, Brian MacMillin Effect of Turbulence on Savonius Rotor Efficiency [электронныйресурс] // http: //www.me.rochester.edu/courses/ME241.gans/SavoniusRotors(7).pdf (датаобращения 18.10.16)
3. Mahmoud N.H., EI-Haroun A.A., Wahba E. An experimental study on improvement of Savonius rotor performance [электронныйресурс] // http://ac.els-cdn.com/S111001681200049X/1-s2.0-S111001681200049X-main.pdf?_tid=f77caf3a-951f-11e6-8095-00000aab0f01&acdnat=1476787701_e632ae06184035ad9b52d9db13533db3 (датаобращения 18.10.16)
4. Rogowski K, Maronsky R. CFD computation of the Savonius rotor // Journal of Theoretical and Applied Mechenics. – 2015. – pp. 37-45
5. Simonds M.H., Bodek A. Perfomence Test of Savonius rotor // http://www.pssurvival.com/ps/Windmills/Performance_Test_Of_A_Savonius_Rotor_1964.pdf (датаобращения 18.10.16)
6. Аскаров Е.С. Ветровая энергетическая установка с ротором Савониуса и неподвижной осью // Вестник машиностроения. - 2012. - № 10. - С. 85-87
7. Ветрогенераторы с вертикальной осью вращения российского производства [электронный ресурс] // http://www.ekopower.ru/vetrogeneratoryi-s-vertikalnoy-osyu-vrashheniya-rossiyskogo-proizvodstva/#rotor-savoniusa (дата обращения 18.10.16)
8. Горелов Д.Н. Экспериментальное исследование энергетических характеристик двухъярусного ротора Савониуса // Теплофизика и аэромеханика, том 12.2005. – № 4. – С. 693-696
9. Даржания И.И. Экспериментальное исследование модели ротора Савониуса [электронный ресурс] // https://istina.msu.ru/conferences/presentations/8793394/ (дата обращения 18.10.16)
10. Пьянков, К.С. Математическое моделирование течения в ветрогенераторах с вертикальной осью / К. С. Пьянков, М. Н. Топорков // Известия РАН. Механика жидкости и газа. - 2014. - № 2. - С. 125-135
11. Редчиц Д.А. Численное моделирование нестационарных турбулентных отрывных течений при обтекании ротора Савониуса // Авиационно-космическая техника и технология, 2008. – № 5 (52). – С.53-58
12. Рожкова Л.Г. Критерии выбора типа, размеров и конструкции ветроколеса вертикально-осевой ветроустановки // Журнал «Актуальные проблемы гуманитарных и естественных наук», 2016. – № 1. – С.98-104
13. Сизов Д.А. Развитие и применение метода дискретных вихрей в задачах аэродинамики и динамики ротора Савониуса [электронный ресурс] // http://fizmathim.com/razvitie-i-primenenie-metoda-diskretnyh-vihrey-v-zadachah-aerodinamiki-i-dinamiki-rotora-savoniusa (дата обращения 18.10.16)