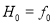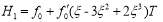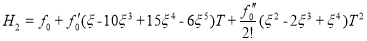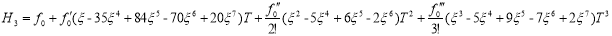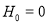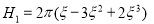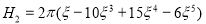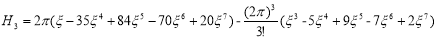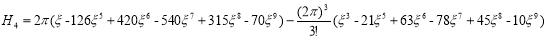Рассмотрена задача приближения периодических функций составными двухточечными многочленами Эрмита. Получены конечные формулы представления этих многочленов, которые используют значения функции и ее производных до n-го порядка включительно в заданной точке. Приведен пример построения составных многочленов Эрмита для периодической функции f(x) = sin x и данные о погрешности приближения.
Ключевые слова: периодические функции, составной двухточечный многочлен Эрмита, формулы аппроксимации функций, погрешность приближения
Введение
Для приближения периодических функций часто применяются тригонометрические функции в форме рядов Фурье. Эти ряды широко используются для решения различных задач, и им посвящена обширная литература [1] — [4].
Особенностью приближения периодических функций рядами Фурье является то, что в них используются тригонометрические функции y= sin x и y= cos x, которые требуют последующего вычисления. Для вычисления этих функций используют разные методы, в частности, разложение их в степенные ряды по формуле Тейлора.
Идея предлагаемого подхода состоит в том, чтобы напрямую использовать многочлены определенного класса для представления периодических функций. В качестве таких многочленов используются двухточечные интерполяционные многочлены Эрмита [5].
1. Постановка и решение задачи
Пусть периодическая функция f(x) с периодом T:
f(x) = f(x+T), (1.1)
определена на интервале (-∞<x<∞) и имеет достаточный набор производных на интервале.
Пусть также в некоторой точке x0 ϵ (-∞,∞) заданы значения функции f(x) и ее производных до порядка m включительно:
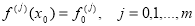. (1.2)
Необходимо построить составной многочлен H(x), который определен на том же интервале (-∞<x<∞) и который удовлетворяет условиям (1.1) и (1.2).
Введем новую переменную ξ, связанную с исходной переменной x соотношением:
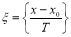, (1.3)
где функция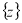 
обозначает дробную часть своего аргумента, т. е. 
.
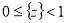Преобразование, выраженное формулой (1.3), сводит неограниченный промежуток изменения периодической функции к промежутку [0,1).
Вследствие того, что производные f(x) также являются периодическими функциями, можно записать, что выполняются условия на правом конце отрезка:
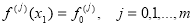, (1.4)
Задача аппроксимации периодической функции на неограниченном промежутке сводится к задаче приближения функции на отрезке с заданными условиями (1.2) и (1.4) на его концах.
Согласно [5, С. 1097] приближающий многочлен Hm(x), удовлетворяющий условиям (1.2) и (1.4), можно представить в виде:
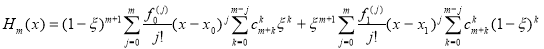. (1.5)
Переходя только к относительной переменной ξ согласно (1.3), учитывая условия выраженные (1.4) и группируя, получим следующее представление для Hm(ξ):
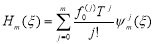, (1.6)
где функции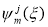 
определены формулой:
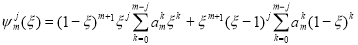, (1.7)
В таблице 1 приведены формулы двухточечного многочлена Hm(ξ), полученные из соотношения (1.6), в которой функции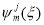 
представлены в виде степеней переменной ξ и s — степень многочлена.
Таблица 1
Формулы для многочлена Hm(ξ)
|
s |
m |
Формулы для Hm(ξ) |
|
1 |
0 |
|
|
3 |
1 |
|
|
5 |
2 |
|
|
7 |
3 |
|
В качестве примера на рис. 1 представлены графики модуля функций .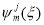
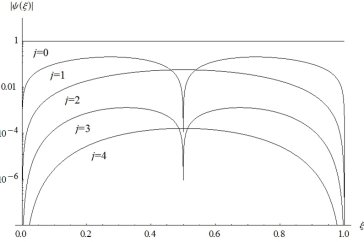
Рис. 1 Зависимость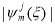 
при j=1,2,3,4 и для m=4
Из графиков видно, что функции 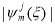обращаются в ноль в крайних точках отрезка [0,1] и быстро убывают с увеличением j.
Полученные результаты можно представить в виде следующей теоремы.
Теорема. Пусть периодическая функция f(x) с периодом T определена на интервале (-∞<x<∞), имеет производные до m-го порядка включительно на этом интервале и заданы условия (1.2) в точке x0 ϵ (-∞,∞). Тогда существует составной многочлен Hm, удовлетворяющий условиям (1.2), который является суперпозицией двухточечного интерполяционного многочлена Эрмита и функции {z}, и который может быть представлен в виде
,
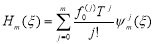где переменная ξ и функции 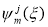определены формулами (1.3) и (1.7), соответственно.
2. Численный пример построения приближающего многочлена
Для периодической функции y = sin x, которая имеет период T=2π, производные определяются соотношением:
.
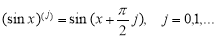Подставляя значения функции и ее производных в формулы, приведенные в таблице 1, получим соотношения для приближающих ее многочленов Hm, которые представлены в таблице 2.
Таблица 2
Формулы приближающего многочлена для функции y = sin x
|
s |
m |
Формулы для многочленаHm(ξ) |
|
1 |
0 |
|
|
3 |
1 |
|
|
5 |
2 |
|
|
7 |
3 |
|
|
9 |
4 |
|
На рис. 2 приведены графики многочлена Hm(x) с использованием исходной переменной x для значений параметра m=0,1,2,3,4 и график функции y = sin x.
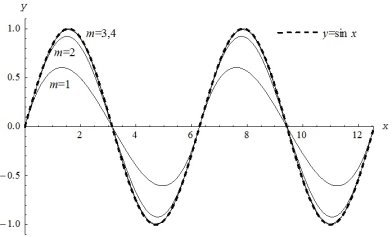
Рис. 2. Приближение функции y = sin x составным многочленом
Из рисунка видно, что с увеличением значения параметра m графики приближающих многочленов монотонно подходят к графику этой функции.
На рис. 3 показаны графики погрешности приближения δ(x), определенной по формуле δ(x)=|f(x)-Hm(x)|, для различных значений параметра m.
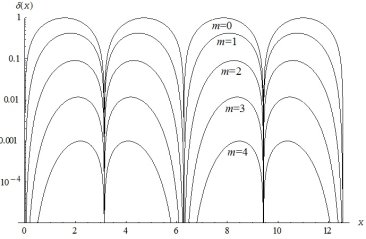
Рис. 3. Погрешность приближения δ(x) для значений параметра m= 0–4
Из графиков видно, что погрешность обращается в ноль на концах отрезка периодичности и уменьшается с возрастанием параметра m.
Заключение
Рассмотрена задача аппроксимации периодических функций составными двухточечными многочленами Эрмита, которая решается путем расширения области применимости данного подхода аппроксимации с конечных отрезков на неограниченные в общем случае промежутки задания функции. В результате решения задачи получены конечные формулы представления периодической функции этими многочленами, которые используют значения функции и ее производных в заданной точке.
Приведен пример представления функции y = sin x последовательностью составных двухточечных многочленов, построенных для этой функции. Результаты исследований погрешности показали, что при определенных условиях составные двухточечные многочлены Эрмита могут использоваться для приближения периодических функций.
В работе использованы материалы доклада, сделанного автором на 18 Саратовской зимней математической школе [6].
Литература:
- Романовский П. И. Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа. — М.: Наука. Гл. ред. физ.-мат. лит., 1980. — 336 с.
- Кудрявцев Л. Д. Курс математического анализа. т. II. — М.: Высшая школа, 1981. — 584с.
- Березин И. С., Жидков Н. П. Методы вычислений. Т. 1 — М.: Физматлит, 1962.– 464 с.
- Воробьев Н. Н. Теория рядов — М.: Наука. Гл. ред. физ.-мат. лит., 1986. — 406 с.
- Шустов В. В. О приближении функций двухточечными интерполяционными многочленами Эрмита // Журнал вычислительной математики и математической физики, 2015, Т. 55, № 7. С. 1091–1108.
- Шустов В. В. О приближении периодических функций составными двухточечными многочленами Эрмита // Современные методы теории функций и их приложения: материалы 18-й Саратовской зимней математической школы, Саратов: изд. ООО «Научная книга», 2016. С. 338–341.
