Обработка почвы является одной из самых энергоемких операций сельскохозяйственного производства. Одним из направлений, позволяющих снизить энергоемкость при обработке почвы является применение конструкций почвообрабатывающих машин с активными рабочими органами. Вместе с тем существующие решения виброприводов с использованием дебалансных вибраторов, кривошипно-шатунных приводов, не получили широкого применения ввиду значительной металлоемкости, невысокой надежности при эксплуатации. Применение гидравлических импульсных приводов ограничивается отсутствием рабочих органов, позволяющих работать в условиях значительного загрязнения и абразивной среды, поэтому разработка рабочих органов, позволяющих передавать импульсное воздействии на почву, и не имеющих узлов, работающих в условиях внешнего трения, является актуальной задачей.
Для решения данной проблемы предложена конструкция рабочего органа культиватора [1, 2, 3, 4] С-образная стойка которого выполнена в виде гибкого трубчатого элемента, представляющего собой герметичную трубу некруглого поперечного сечения (см. рис. 1).
Принцип действия рабочего органа заключается в следующем. При подаче давления в полость стойки 2 через штуцер рабочей жидкости, либо воздуха, происходит деформация сечения, в результате этого её свободный конец с рыхлительной лапой 1 совершает перемещение. При подаче пульсирующего давления рыхлительная лапа совершает колебательные движения с определенной амплитудой и частотой, которые зависят от параметров подаваемого давления. Изменяя параметры давления, можно задать различные режимы колебания, что позволит снизить тяговое сопротивление.
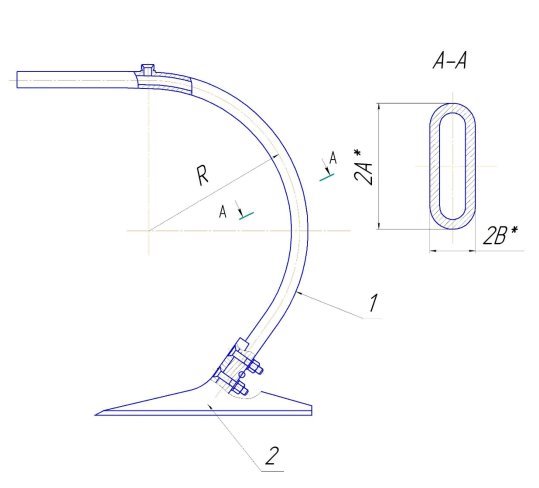
Рис. 1. Рабочий орган культиватора со стойкой в виде гибкого трубчатого элемента: 1 — гибкий трубчатый элемент; 2 — рыхлительная лапа
Одной из задач является определение напряженно-деформированного состояния гибкого трубчатого элемента в случае обратного соотношения осей сечения, когда большая ось поперечного сечения лежит в плоскости кривизны элемента. Такая ориентация сечения придет жесткость стойке и позволяет изменить направление импульсного воздействия на почву при культивации.
Ниже на основании полубезмоментной теории оболочек [5, 6] приведен расчет гибкого трубчатого элемента с обратным соотношением осей.
Напряженно-деформированное состояние трубчатого элемента описывается дифференциальными уравнениями:
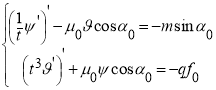 (1)
(1)
В этих уравнениях искомыми являются функции ψ и ![]() безразмерной координаты η:
безразмерной координаты η:
![]() ;
; ![]() (2)
(2)
где s — длина меридиана, отсчитываемого от выбранного начала координат;r– «приведенный радиус» сечения; П– периметр поперечного сечения срединой поверхности трубчатого элемента.
Функция ![]() — угол поворота в точке сечения η, то есть, изменение начального угла наклона касательной α0(η):
— угол поворота в точке сечения η, то есть, изменение начального угла наклона касательной α0(η):
![]() (3)
(3)
Функция, ψ(η) характеризующая напряжения в стержне, имеет вид:
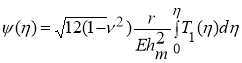 (4)
(4)
где ν — коэффициент Пуассона материала трубки; Е — модуль упругости материала трубки;hm– толщина стенки пружины в точке с координатой η=π/2; ![]() — нормальное усилие на единицу длины поперечного сечения. Величины с индексом 0 относятся к недеформированному состоянию.
— нормальное усилие на единицу длины поперечного сечения. Величины с индексом 0 относятся к недеформированному состоянию.
Функция t(η) зависит от закона изменения толщины стенки и определяется следующим образом:
![]() (5)
(5)
где h(η) — толщина стенки сечения.
Параметры q, μ и m учитывают соответственно нормальное давление p, кривизну оси и ее изменение:
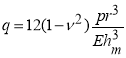 ,
, 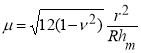 ,
, ![]() (6)
(6)
где R — радиус центральной оси трубки.
Перерезывающая сила в сечении с r=1 от единичной нагрузки, представлена в (2) функцией:
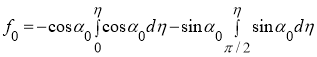 (7)
(7)
Уравнения (1) справедливы, если материал трубчатого элемента упругий и однородный, угол поворота мал сравнительно с единицей, размеры поперечного сечения малы сравнительно с R.
В уравнениях (1) формa средней линии поперечного сечения задается посредством функций cosα и sinα. Вследствие симметрии сечения относительно осей x и z достаточно определить данные функции на участке ![]() , при этом выражая значения угла α(η) получим (рис.2):
, при этом выражая значения угла α(η) получим (рис.2):
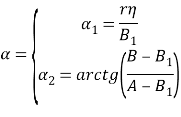 (8)
(8)
В выражении (8):
![]() ,
, ![]() .
.
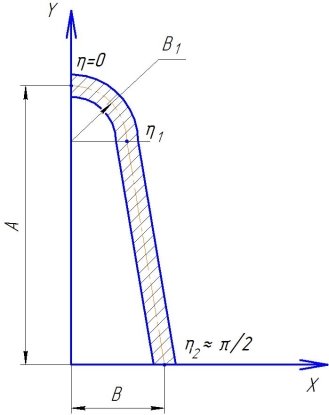
Рис. 2. Модель сечения стойки
Введем обозначения:
![]() ,
,![]() (9)
(9)
Тогда система уравнений (1) в нормальной форме запишется в виде:
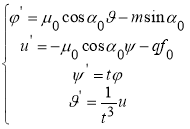 (10)
(10)
Система уравнений дополнена граничными условиями:
![]() ,
, 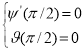 (11)
(11)
В линейном приближении искомые функции представим в виде суммы двух частей пропорциональных соответственно параметру изменения кривизны m и параметру нормального давления q:
![]() ,
,![]() (12)
(12)
В результате подстановки выражений (12) в систему (1), получим две системы:
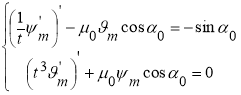 ,
,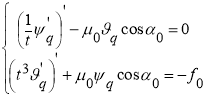 (13)
(13)
Используя алгоритм решения системы (1) определяем из систем (13) функции ![]() ,
,![]() ,
,![]() ,
,![]() .
.
Для решения полученной краевой задачи применен метод стрельбы [6], написана программа в среде МАТLАВ, интегрирование задач Коши проводилось методом Рунге-Кутта 4 порядка точности с использованием стандартного решателя ode45.
Для стойки, работающей в режиме свободного хода, когда свободный конец трубки под действием нормального давления имеет возможность свободно перемещаться, система разрешающих уравнений дополняется условием равенства нулю момента в поперечном сечении трубки:
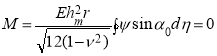 (14)
(14)
Из выражения (12) с учетом (14) определяем относительный угол раскрытия пружины:
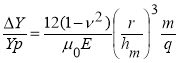 , где
, где 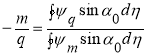 (15)
(15)
Результаты сопоставления расчетной чувствительности с экспериментальными данными для пружин с переменной по периметру сечения толщиной стенки и результатами расчета энергетическим методом.
Формулы для вычисления продольных и поперечных напряжений в любой точке наружного и внутреннего контура сечения:
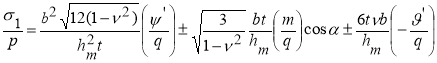 (16)
(16)
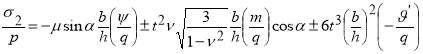 (17)
(17)
Таким образом, получена математическая модель напряженно-деформированного состояния гибкого трубчатого элемента в случае обратного соотношения осей сечения, что позволит в дальнейшем получить решить вопрос выбора рациональных параметров гибких трубчатых элементов данного типа.
Литература:
- Устинов Н. Н. Математическая модель активного рабочего органа культиватора со стойкой в виде гибкого трубчатого элемента / Н. Н. Устинов, А. А. Маратканов, Н. И. Смолин // Современные проблемы науки и образования. — 2015. — № 1; URL: http://www.science-education.ru/121–17908 (дата обращения: 18.03.2015).
- Маратканов А. А. Экспериментальное определение характеристик активного рабочего органа культиватора со стойкой в виде гибкого трубчатого элемента / А. А. Маратканов, Н. Н. Устинов // Вестник Алтайского государственного аграрного университета. — 2015. — № 4(126). — С.102-105.
- Устинов Н. Н. Рабочий орган культиватора / Сельский механизатор. — 2015. — № 12. — С. 30–31.
- Пат. 116000 U1, Российская Федерация. МПК А01В 39/20, А01В 35/20. Рабочий орган культиватора / А. А. Маратканов, Н. И. Смолин, С. Н. Кокошин, Н. Н. Устинов. Заявители и патентообладатели: ФГОУ ВПО «Тюменская государственная сельскохозяйственная академия» (RU). — Заявл. 03.05.2011, опубл. 20.05.2012. Бюл. № 14. -3 c.:ил.
- Аксельрад Э. Л. Гибкие оболочки. М., Наука, 1976. — 376 с.
- Устинов Н. Н. Расчет и проектирование тонкостенных манометрических трубчатых пружин с переменной по периметру сечения толщиной стенки: автореф. дис. канд. техн. наук: 05.22.06 / Устинов Николай Николаевич.– Тюмень.: ТГУ, 2004.– 21 с.

