An approach that allows to design a frequency filter with a simple switching of the cutoff frequency while maintaining high precision filter characteristics. An example of calculating nominal circuit elements.

Key words: filter, switching, cut-off frequency, electronic key

При проведении исследований, связанных с получением и обработкой измерительных данных в аналоговой форме, часто требуется оперативно изменять полосу пропускания фильтра для оценки спектрального состава сигнала.

По сравнению с каскадными фильтрами в цепочечных фильтрах на основе конверторов с операционными усилителями (ОУ) удается достаточно просто коммутировать элементы схемы при сохранении высоких точностных характеристик.

Конверторные фильтры на основе LC-прототипа [1] обладают низкой чувствительностью характеристик к изменению внешних условий и нестабильности параметров электрорадиоизделий.

Схема обобщенного конвертора (рис. 1) обладает эквивалентным входным сопротивлением, описываемым выражением (1).

(1)

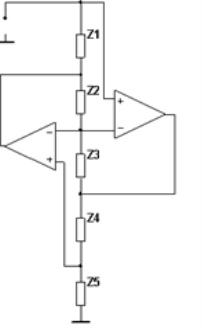
Рис. 1. Схема обобщенного конвертора

Соотношение (1) позволяет менять эквивалентное сопротивление путем изменения соотношения резисторов, расположенных на соседних позициях в конверторе. Например Z4 и Z5, Z4 и Z3 и др.

В прецизионных фильтрах необходимо существенно уменьшить влияние сопротивления открытого ключа при перестройке параметров фильтра. Для этого электронные ключи могут быть размещены или последовательно с очень большим входным сопротивлением ОУ (рис.2а) или в цепи обратной связи ОУ (рис.2б) когда влияние уменьшается в р раз, где коэффициент обратной связи, а k — коэффициент усиления ОУ.

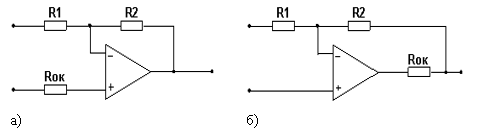
Рис. 2. Способы включения электронного ключа последовательно с входом ОУ (а) и в цепи обратной связи (б)

Это требование легко реализуется при конверторной реализации лестничных фильтров.

В качестве примера рассмотрим подход к проектированию фильтра нижних частот (ФНЧ), которые могут быть симметричными (рис. 3а) с и несимметричными (рис.3б) с , где — сопротивление генератора (источника сигнала), – сопротивление нагрузки.

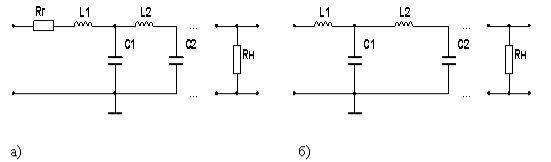
Рис. 3. Симметричный (а) и несимметричный (б) лестничный прототип конверторного фильтра

В справочных данных на лестничные LC-прототипы фильтров приводятся нормированные безразмерные значения и [2].Для получения действительных значений и необходимо провести денормирование для реальных значений частоты среза и по формулам (ФНЧ):

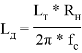,(2)

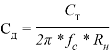.(3)

Применяя метод частотного преобразования можно избавиться от индуктивностей, которые обладают низкой точностью и стабильностью и большими габаритами, особенно на низких частотах. Для этого необходимо поделить сопротивления всех элементов LC-прототипа на на , где k – масштабный коэффициент, имеющий размерность времени; –текущая частота.

В результате частотного преобразования индуктивности преобразуются в резисторы R, емкости – в суперёмкости D и резисторы , – в емкости и согласно формулам::

,(4)

,(5)

(6)

где i — номер индуктивности, j — номер емкости в LC-прототипе.

Неоднозначность преобразования на частоте =0 приводит к тому, что для симметричного фильтра происходит искажение амплитудно-частотной характеристики (АЧХ) ФНЧ. Из-за конденсатора на входе фильтра постоянная составляющая сигнала фильтром не пропускается в отличие от исходного LC-прототипа. Поэтому в конверторных ФНЧ необходимо использовать несимметричные LC-прототипы (рис. 3б) с =0, которые лишены этого недостатка. Тогда после частотного преобразования ФНЧ примет вид рис. 4, где – супер емкость [4].

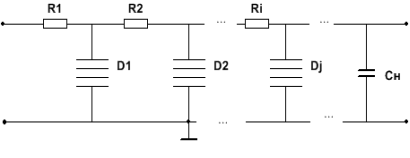
Рис.4. Конверторный ФНЧ после частотного преобразования

Подставляя (2) и (6) в (4), найдем:

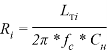(7)

Согласно (1) для реализации суперемкости необходимо использовать схему обобщенного конвертора с размещением конденсатора на трех возможных позициях: 1,3; 1,5 и 3,5. Реально используются только варианты с размещением конденсатора на 1 позиции, т. к. при этом исключается попадание в цепь прохождения полезного сигнала накопленной в конверторе погрешности по постоянному току. Тогда возможны два варианта выполнения суперемкости (рис. 5).

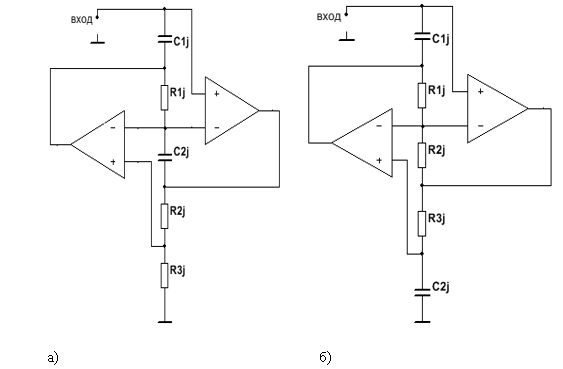
Рис. 5. Реальные варианты исполнения суперемкости с расположением C2j на третьей (а) или пятой позиции (б)

При таком сочетании элементов входное сопротивление конвертора является частно зависимым отрицательным сопротивлением(ЧЗОС) или суперемкостью:

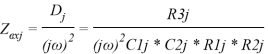для рис. 5а,(8)

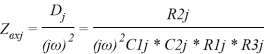для рис. 5б.

Для примера рассмотрим вариант рис.5а, когда величину можно менять соотношением R2j и R3j.

Требуемое изменение частоты среза можно провести не изменяя сопротивление резисторов , а только изменяя эквивалентное сопротивление ЧЗОС и нагрузки. Пусть исходная расчетная частота ФНЧ и требуется увеличить ее в 2 раза. Тогда, согласно (7), чтобы не менять резисторы , необходимо в 2 раза увеличить емкость . Таким образом

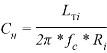(9)

Рассмотрим как при этом меняются номиналы элементов в ЧЗОС. Подставим (3) и (6) в (5).

Тогда суперемкость

.(10)

С другой стороны, определяется выражением (8). Как правило в конверторе выбирается С1j=C2j=Cj и из сравнения (8), (9) и (10) получаем:

,

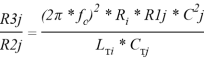т. е. пропорционально квадрату частоты среза .

Схема коммутации резисторов для 4-х значений частоты среза ФНЧ на основе суперемкости рис.5а показана на рис.6а, где ЭК-электронные ключи, а x1 и x0- двоичный код для управления коммутацией.

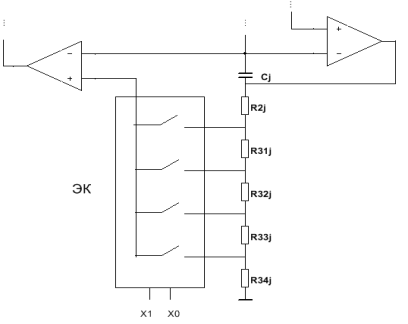
Рис. 6. Схема коммутации резисторов суперемкости

На рис. 6 R31j+R32j+R33j+R34j=R2j. Система уравнений для расчета резисторов выглядит следующим образом:

R2j=1*(R31j+R32j+R33j+R34j)

R2j+R31j=4*(R32j+R33j+R34j)

R2j+R31j+R32j=16*(R33j+R34j)

R2j+R31j+R32j+R33j=64*R34j

Для изменения с высокой точностью емкости требуется выполнить ее на базе обобщенного конвертора в режиме умножителя емкости с конденсатором на первой позиции и резисторами на остальных. Тогда:

(11)

Так как прецизионные конденсаторы выпускаются относительно небольших номиналов, то благодаря конверторной реализации можно получить прецизионные емкости широкого диапазона номиналов благодаря изменению соотношения резисторов (11), например R3 и R4.

Схема коммутации резисторов в нагрузке аналогична рис.6, но в системе уравнений для резисторов R3, R41, R42, R43, R44 в правой части уравнений должны быть множители 1, 2, 4 и 8.

Предложенная методика позволяет подключать сопротивления ключей мультиплексора последовательно к входному сопротивлению ОУ, что практически исключает их влияние на точностные параметры фильтра.

Литература:

1. Ильенков В. Г., Кузнецов С. Н., Иванов А. А. — Радиотехника, 1990, № 11, c. 86, 87.
2. Зааль Р. Справочник по расчету фильтров — М. Радио и связь, 1983. – 753 с.
3. Букашкин С. А. и др. Справочник по расчету и проектированию ARC-схем / Под ред. Ланне А. А. — М.: Радио и связь, 1984. – 368 с.
4. Хоровиц П., Хилл У. Искусство схемотехники — М.: БИНОМ, 2014. – 704 с.