Выполнение вариантов единого государственного экзамена предполагает умение сконцентрироваться на полученном задании, внимательность к его выполнению, способность определять главное в большом потоке полученной информации, на быстрый переход от одного блока заданий к другому, и, конечно же, на владение приобретенными знаниями. На сегодняшнее время старшекласснику недостаточно просто «выучить некоторое количество данного в учебнике материала», необходимо приобрести широкий кругозор в процессе усвоения различных тем. Анализ содержания математических дисциплин определяет их главные отличительные признаки:
– преобразование выражений к конкретному правильному результату;
– владение формулами и теоремами для быстрого выполнения заданий;
– высокая степень самостоятельной работы.
ЕГЭ по математике позволяет максимально определить сформированность математических компетенций, которые закреплены требованиями Федерального компонента государственного образовательного стандарта среднего (полного) общего образования по математике. Школьный математический курс содержит изучение текстовых задач, являющихся неотъемлемыми при оценивании общей математической подготовки учащихся на ЕГЭ [2]. Данные задачи ориентированы на умение правильно составлять уравнения. Текстовые задачи подразделяются на несколько типов задач, которые для наглядности приводятся в таблице 1.
Таблица 1
|
Текстовые задачи |
ДВИЖЕНИЕ |
|
|
РАБОТА |
| |
|
ПРОЦЕНТЫ |
| |
|
КОНЦЕНТРАЦИЯ |
|
Анализ результатов выполнения заданий по математике приводит к выводу, что способность решать текстовые задачи является основополагающей в процессе подготовки к экзамену. В ходе решения различных задач практического характера были выделены основные этапы, представленные в таблице 2 [1].
Таблица 2
|
Э Т А П Ы |
Перевод исходных данных задачи на язык математики |
|
Решение полученной математической задачи | |
|
Интерпретация найденного решения |
Последний этап позволяет выяснить практический смысл найденных результатов задачи. Текстовые задачи, как говорилось выше, вырабатывают умение составлять уравнения, для которого предлагается следующий алгоритм: составлять уравнение → решать → получать значение.
Но существует ряд проблем, с которыми сталкиваются учащиеся при решении данных заданий. Текстовые задачи содержат максимально возможное число учебных материалов сразу нескольких классов, из-за чего ученики во многих случаях не способны актуализировать необходимые знания для решения задач. А в действительности необходимо знать лишь несколько формул:
- формула взаимосвязи пройденного расстояния со скоростью и временем, потраченным на преодоление этого расстояния;
- формула связи совершенной работы с производительностью и временем, потраченным на выполнение данной работы;
- правила, используемые при решении задач на проценты, и умение составлять пропорции.
- Задачи на движение
Довольно часто в условии задачи не встречается дополнительных оговорок. В таком случае движение будем считать равномерным, тогда пройденный путь будем искать по следующей формуле: S=V*t, где S — расстояние, пройденное телом; V — скорость движения тела, t — время движения тела.
Все величины берутся положительными: S>0, V>0, t>0. Данные величины обязательно записываем в одной системе координат:
|
Расстояние |
Скорость |
Время |
|
километры |
километр/час |
час |
|
метры |
метр/секунд |
Секунда |
|
метры |
метр/минут |
минута |
- Движение по прямой
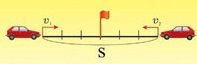
Задачи, в которых речь идет о равномерном движении, определяют вероятность возникновения следующих условий. Если первоначальный промежуток между предметами равен S, а скорость объектов V1 и V2, то:
а) при встречном движении тел время, через которое они встретятся, будет равно ![]() ;
;
б) при движении объектов в одну сторону (V1>V2) время, через которое первый объект догонит второй, находится как ![]() .
.
- Движение по замкнутой дороге
Если в условии задачи говорится, что дорога замкнута и ее длина определяется как S, а скорости объектов V1 и V2, то:
а) при совершении движения тел в одном и том же направлении время между их встречами находится по формуле ![]() (V1>V2);
(V1>V2);
б) при совершении движения тел в разных направлениях время между их встречами находится по формуле ![]() .
.
- Движение по реке
Если в условии говорится о движении по течению реки, то скорость, с которой плывет тело, находится по следующей формуле Vпо течению =Vсобств+Vтечен.
Если объект двигается против течения реки, то его скорость находится как Vпротив течения =Vсобств-Vтечен.
Скорость самого объекта в неподвижной реке определяется ![]() , а скорость течения реки равна
, а скорость течения реки равна ![]() . Скорость, с которой совершает передвижение плот находится как скорость течения реки.
. Скорость, с которой совершает передвижение плот находится как скорость течения реки.
- Движение протяженных тел
При движении двух объектов навстречу друг другу скорость одного объекта относительно другого определяется как V1+V2. При движении двух объектов в одну сторону со скоростью V1, V2, скорость одного объекта относительно другого равна V1-V2(V1>V2).
- Средняя скорость
Чтобы определить среднюю скорость движения объекта, необходимо все пройденное расстояние разделить на общее время движения ![]() .
.
- Задачи на работу
В данных задачах обычно используются три величины: время t, в течение которого совершена работа; производительность N — работа, совершенная в единицу времени; работа A, произведенная в единицу времени.
Данные величины объединяются формулой A=N*t. Отсюда находим N=A/t, t=A/N. Все величины берутся положительные.
Задачи на работу делятся на два типа: с явным объемом работы (в условии указывается объем работы или необходимость его поиска) и неявным объемом работы (в условии объем работы не обозначается, в таких случаях он принимается за 1).
- Задачи на проценты
- Части и проценты
Чтобы найти проценты от данного числа, необходимо: а) записать с помощью дробей проценты; б) умножить данное число на эту дробь
(aсоставляет p % от b) ![]()
- Процентное сравнение величин
При выполнении сравнения заданных величин за 100 % берется та, с которой производится сравнение. В задачах на проценты первоначально необходимо выяснить, какую из данных величин взять за 100 %.
- Сложные проценты
Формула «сложных процентов» для двухкратного изменения находится A2=A0(1±0,01p1)(1±0,01p2), где A0 — первоначальное значение величины; A, A2 — новое значение величины A после ее двухкратного процентного изменения; ![]() ,
, ![]() — проценты изменения величины A.
— проценты изменения величины A.
- Задачи на концентрацию
Массовой концентрацией ![]() вещества A в смеси называется отношение массы
вещества A в смеси называется отношение массы ![]() этого вещества к общей массе M:
этого вещества к общей массе M: ![]() ;
; ![]() =
=![]() *M; M =
*M; M =![]() .
.
Массовым процентным содержанием вещества A в данной смеси называется величина ![]()
Если смесь массы M состоит из вещества A и B, то имеют место следующие равенства
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Но бывают задачи, которые решаются не по данным формулам, а с помощью логических рассуждений.
Задача 1.
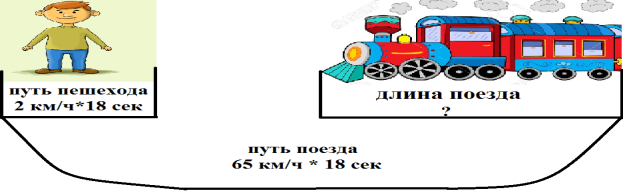
Поезд двигается со скоростью 65 км/ч, он проезжает мимо пешехода, двигающегося параллельно железнодорожным путям со скоростью 2 км/ч навстречу поезду за 18 секунд. Необходимо определить длину поезда в метрах, если учитывать, что движение поезда равномерно.
Такая задача относится к типу I — задач на движение. Покажем первый способ ее решения. Для наглядности продемонстрируем рисунок.
-
Из рисунка можно сделать вывод, что длина поезда находится следующим образом:
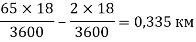 .
.
- Но условие задачи требует найти длину поезда в метрах, для этого выполняем следующую: 0,335*1000=335 м.
Ответ найден, однако, задача решается значительно быстрее, если воспользоваться определением скорости сближения. Скорость сближения — это расстояние, на которое сближаются объекты за единицу времени. Единицей измерения является км/ч, м/с. При равномерном движении объектов с разными скоростями расстояние между данными объектами либо увеличивается, либо уменьшается на одно и то же число единиц [3].
- Если в условии задачи сказано, что объекты совершают встречное движение со скоростью V1 и V2, то скорость сближения находится как Vсближ=V1+V2.
- Если объекты совершают движение в одном направлении со скоростью V1 и V2, то скорость сближения находится как Vсближ=V1-V2.
Тогда ответ в данной задаче может быть получен следующим способом.
- Определим, как быстро сближаются поезд и пешеход, двигаясь навстречу друг другу
65+2 = 67 км/ч.
- Необходимо по условию задачи длину поезда найти в метрах, следовательно совершаем следующее действие
67 км/ч = 67·1000/3600 = 670/36 = 335/18= (м/с).
- Для нахождения длины поезда необходимо скорость сближения пешехода и поезда умножить на затраченное время
(335/18)·18 = 335 (м) — длина поезда.
Данную задачу можно решить любым предложенным способом, однако, мониторинг решения задач ЕГЭ показывает, что большинство учащихся приходит к неправильному варианту ответа еще и по причине невыполнения требований условия задачи: нахождение длины поезда в метрах [2].
Ответ: 335 метров.
Большее затруднение у учащихся вызывает следующая задача.
Задача 2.
Поезд двигается со скоростью 90 км/ч, он проезжает мимо лесополосы, длина которойравна 500 метров. Поезд затрачивает время равное 1 минуте. Найдите длину поезда в метрах, если принимать его движение за равномерное.
Решение.
Чтобы решить такую задачу, нужно мысленно вообразить, как поезд совершает движение мимо леса. Если считать, что мы находимся в одном из вагонов поезда, то приближаясь к лесу, мы полностью проезжаем его (это расстояние равно 500 метров), но весь поезд еще не окончательно проезжает лес, так как с концом леса еще не поравнялся последний вагон, то есть поезду необходимо пройти расстояние, которое будет равно его длине.
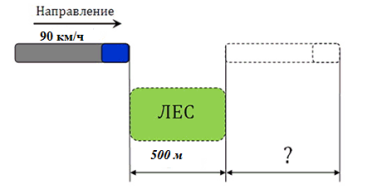
По условию задачи поезд затрачивает время равное 1 минуте для прохождения лесополосы. Следовательно можно найти расстояние, которое он преодолевает за указанное время:
![]()
Таким образом, длина поезда находится как 1,5–0,5 = 1 км. А так как по условию необходимо указать длину поезда в метрах, проделываем следующую операцию:
1*1000 =1000 метров.
Ответ: 1000 метров.
Задача 3.
9 рубашек дешевле одного костюма на 19 %, на сколько процентов 13 рубашек дороже одного костюма?
Решение.
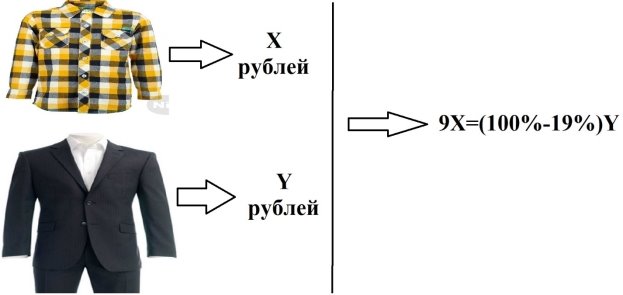
Рисунок говорит нам о том, что цену одной рубашки обозначили за x, а цену одного костюма — y. Условие задачи позволяет понять, что общая стоимость 9 рубашек дешевле стоимости одного костюма на 19 %, а значит, что стоимость 13 рубашек составляет 100 %-19 %=81 % стоимости одного костюма. Следовательно, можем составить уравнение:
9х=81/100y
9х=0,81y
x=0,09y
Записанное уравнение позволяет определить, что стоимость одной рубашки составляет некоторую часть стоимости одного костюма. Условие задачи требует найти процентное отношение 13 рубашек к стоимости одного костюма. Следовательно умножим обе части равенства на 13:
13x=1,17y.
Обозначим стоимость одного костюма за 100 %, тогда получается, что стоимость 13 рубашек больше стоимости одного костюма на 17 %.
Ответ: 17 %.
Рассмотрим еще одну задачу, которая на первый взгляд оказывается очень сложной для многих учащихся.
Василий Иванович плывет по океану на яхте, средняя скорость которой равна 27 км/ч. Доплыв до заданного пункта, он решил вернуться обратно, но только уже на самолете, скорость которого 513 км/ч. Необходимо найти среднюю скорость Василия Ивановича, с которой он путешествовал на всем пути. Ответ нужно дать в км/ч.
Задача решается очень быстро, если помнить формулу нахождения средней скорости ![]() . Данные задачи подставляем в формулу и находим
. Данные задачи подставляем в формулу и находим ![]() =51,3 км/ч.
=51,3 км/ч.
Но довольно часто учащиеся испытывают затруднения на экзамене, так как из-за переживаний не способны вспомнить нужную формулу. Поэтому рассмотрим следующий способ нахождения ответа задачи по всем известной формуле. Для этого воспроизведем формулу скорости V![]() , необходимо определить весь путь, который прошел Василий Иванович и общее время, которое потребовалось на прохождение всего участка. Данные задачи позволяют найти время, которое Василий Иванович прибывал в пути на яхте t1
, необходимо определить весь путь, который прошел Василий Иванович и общее время, которое потребовалось на прохождение всего участка. Данные задачи позволяют найти время, которое Василий Иванович прибывал в пути на яхте t1![]() часов, а время, за которое он долетел на самолете обратно, равно t2
часов, а время, за которое он долетел на самолете обратно, равно t2![]() часов. Таким образом, можно сделать вывод, что весь путь S=2S, а общее время в пути равно tобщ=t1+t2=
часов. Таким образом, можно сделать вывод, что весь путь S=2S, а общее время в пути равно tобщ=t1+t2=![]() . Подставляем полученные значение пути и времени в формулу нахождения скорости:
. Подставляем полученные значение пути и времени в формулу нахождения скорости:
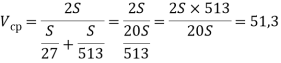 км/ч
км/ч
Ответ: 51,3 км/ч
Указанные выше особенности решения текстовых задач позволяют качественно и быстро решить задачи такого типа, повысить самооценку учащихся, создать благоприятный климат на экзамене.
Литература:
- Миронова С. В., Напалков С. В., Нестерова Л. Ю. О некоторых способах организации продуктивной математической деятельности учащихся в дополнительном образовании // Технологии продуктивного обучения математике: традиции и инновации: сборник статей участников Всероссийской научно-практической конференции с международным участием (посвящается памяти профессора М. И. Зайкина) / Научный редактор С. В. Миронова, ответственный редактор С. В. Напалков; Арзамасский филиал ННГУ. — Арзамас, 2016. — С. 70–75.
- Нестерова Л. Ю. Совокупности специализированных задач для подготовки учащихся к итоговой аттестации по математике // Задачные конструкции математического развития школьников: сборник статей участников научно-методического семинара / Под общей редакцией С. В. Арюткиной, С. В. Напалкова. — 2015. — С. 51–53.
- http://elhow.ru/ucheba/matematika/kak-najti-skorost-sblizhenija