Одним из фундаментальных вопросов современной теории поиска объектов является выбор модели поисковых усилий (поискового потенциала) поисковой системы и поисковых единиц, её составляющих. С одной стороны, должно обеспечиваться построение общей теории поиска объектов, а с другой – должны отражаться особенности средств наблюдения, которыми оснащены поисковые единицы, для получения возможности формирования оптимального управления ими. Разработанные модели (например, в [1] – [4]) соответствуют пуассоновскому потоку обнаружений и определяются интенсивностью поиска. Такие модели не отражают особенности средств наблюдения, которыми оснащены поисковые единицы, и не допускают возможности непосредственного формирования оптимального управления ими.
Таким образом, задача выбора и обоснования классификационных признаков математических моделей поисковых усилий, построенных на основе траекторного подхода, для систем, состоящих из группы поисковых единиц (в общем случае не являющихся неподвижными), является актуальной.
Проведём анализ пригодности следующих основных принятых в теории РТС классификационных признаков для использования в общей теории поиска объектов многопозиционными системами.
1. По диапазону волн. Применение этого признака обусловлено тем, что РТС могут использовать радиоволны различной длинны.
2. По типу объекта-носителя РТС. Этот признак предполагает учёт размещения элементов РТС на кораблях, самолётах, на борту космических аппаратов и т.д.
3. По источникам сигналов. Учитывает наличие или отсутствие источников излучения в составе средств наблюдения и (или) искомого объекта. По этому признаку объекты процесса поиска делятся на два типа - активного и пассивного, а сами системы классифицируются в зависимости от сочетания типов составляющих их объектов.
4. По структуре измерительных пунктов. В зависимости от назначения РТС могут иметь различную структуру: распределённого, разнесённого и гибридного типов.
5. По виду первичных измеряемых параметров. В теории РТС по этому признаку выделяют дальномерные (латерационные), суммарно-дальномерные, разностно-дальномерные и угломерные системы.
Существенным отличием поисковых систем является их направленность не на измерение параметров объектов, а на их поиск. С другой стороны, в теории РТС каждому измеряемому параметру ставится в соответствие линия положения на плоскости или поверхность положения в пространстве. Пусть каждому типу средств наблюдения поисковых единиц соответствует поверхность положения в n-мерном пространстве поиска. По аналогии с РТС можно рассматривать, например, следующие типы средств наблюдения: сферические, плоскостные, гиперболоидные, эллипсоидные.
Рассмотрим пример построения математической модели поисковых усилий системы, состоящей из группы поисковых единиц, оснащённых сферическими средствами наблюдения. Пусть задано некоторое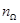 
- мерное нормированное пространство поиска 
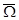с нормой 
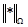. В пространстве 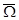определена область поиска 
.
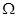Будем полагать, что поисковая система является групповой, т.е. состоит из нескольких поисковых единиц. Без ограничения общности полагаем, что поисковая система (ПС) включает J поисковых единиц (ПЕ), динамика векторов состояния которых в пространстве 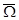описывается непрерывным марковским процессом с моделью вида:
, 
, 
, 
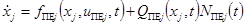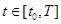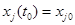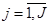, (1)
где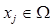 
, 
,
, 
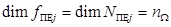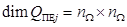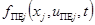– заданные функции, 
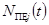– векторы формирующих шумов, 
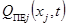– матрицы интенсивностей, 
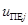– вектор управления состоянием j-ой поисковой единицы в пространстве , 
, 
.
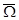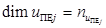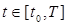Положение каждого k-го (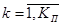
) нового объекта поиска (ОП) в области 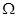задаётся начальной плотностью распределения 
, 
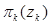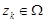. Их динамика в пространстве состояний объектов поиска 
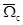описывается непрерывным марковским процессом, модель которого имеет вид:
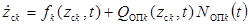, (2)
где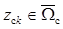 
, 
,
, 
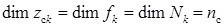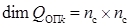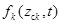– заданные функции, 
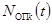– векторы формирующих шумов, 
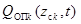– матрицы интенсивностей, 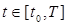. В общем случае 
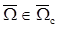. Полагается, что области поиска 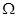, динамика целей и начальные плотности распределения положения целей 
, 
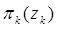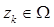таковы, что
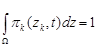(3)
для всех 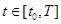. Пусть 
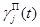– функции, определяющие режим поиска ОП средствами наблюдения, 
, 
; 
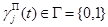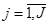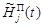и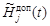 
– функции, определяющие функционирование соответственно 
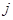-го средства наблюдения, и их допустимые множества.
Тогда ограничения, учитываемые в процессе поиска, формируются на основе выражений:
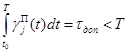, (4)
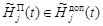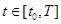, . (5)
Задачу оптимального управления поиском динамических объектов можно сформулировать в следующем виде:
найти план функционирования ПС
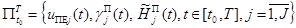, (6)
обеспечивающий экстремум функционала
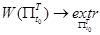, (7)
в условиях ограничений (1) – (5) .
Для задачи (1) – (7) построим математическую модель поисковых усилий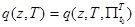 
групповой поисковой системы, состоящей из группы поисковых единиц, оснащённых сферическими средствами наблюдения.
На основе траекторного подхода к описанию поисковых усилий [5] – [7], представим поисковое усилие по поиску k-го ОП для заданной точки z области поиска в следующем виде:
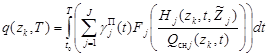, (8)
где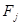 
– функции, характеризующие плотности поисковых усилий соответствующих средств наблюдения, 
, 
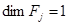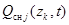– функции, характеризующие интенсивность шумов в канале поиска соответствующих средств наблюдения, 
, 
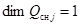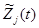— траектории поиска соответствующих средств наблюдения, которые являются одними из управляемых переменных, влияющих на значение заданного показателя эффективности поиска, 
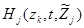– «сигнальные» функции каналов поиска соответствующих средств наблюдения, 
.
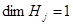Поскольку поставлена задача для пространства 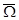построить математическую модель поисковых усилий 
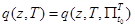групповой поисковой системы, состоящей из группы поисковых единиц, оснащённых сферическими средствами наблюдения, то функции 
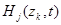должны описывать поверхность положения в виде сферы в пространстве поиска:
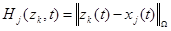. (9)
В свою очередь, функции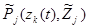 
для пространства 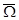по определению могут быть представлены в виде:
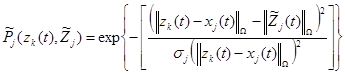, (10)
где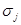 
– постоянные величины модели поисковых усилий, характеризующие размеры элементов разрешения соответствующих средств наблюдения.
Подставляя (9), (10) в (8), получим
.
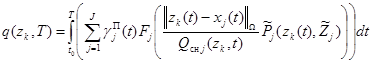Таким образом, предложенная классификация средств наблюдения обобщает принятую в теории РТС классификацию по признаку, связанному с видом первичных измеряемых параметров, как для поисковых систем в целом, включающих не только радиотехнические средства наблюдения, так и для систем с пространством поиска, включающем измерения не только по координатам и скорости объектов.
Библиографический список
- Абчук, В.А. Поиск объектов / В.А. Абчук, В.Г. Суздаль. – М. : Советское радио, 1977. – 336 с.
- Хеллман, О. Введение в теорию оптимального поиска / О. Хеллман. – М. : Наука, 1985. – 248 с.
- Ким, Д.П. Методы поиска и преследования подвижных объектов / Д.П. Ким. – М. : Наука, 1989. – 336 с.
- Аркин, В.И. Равномерно-оптимальные стратегии в задачах поиска / В.И. Аркин // Теория вероятностей и её применения. – 1964. – Т. 9. – № 4. – С. 746–753.
- Строцев, А.А. Критерий максимума апостериорной вероятности обнаружения цели к заданному времени / А.А. Строцев // Известия вузов. Радиоэлектроника. – 2002. – Т.45. – № 10. – С. 34–41.
- Строцев, А.А. Совместное оптимальное управление поиском и наблюдением за условно детерминированными динамическими объектами в импульсной многоканальной измерительно-поисковой системе / А.А. Строцев // Известия вузов. Радиоэлектроника. – 2004. – Т.47. – № 9. – С.22–29.
- Строцев, А.А. Синтез оптимального управления многопозиционной информационной системой при поиске группы динамических объектов / А.А. Строцев, И.Л. Иващенко // Изв. вузов. Радиоэлектроника. – 2005. – Т. 48. – № 10. – С. 37–45.
- Discenza, J.H. Optimal survivor search with multiple states / J.H. Discenza, L.D. Stone // Operations Research. . – 1981. – V. 29. – № 2.
