Введение
С изобретением Марком Цукербергом социальной сети Facebook мир шагнул в новую эпоху развития. «Мы жили в деревнях. А потом в городах. Теперь будем жить в интернете» — эти слова из фильма «Социальная сеть» стали пророческими, ведь действительно, на сегодняшний день невозможно представить свою жизнь без социальных сетей. К примеру, в одном только ВКонтакте ежемесячная аудитория составляет 46,6 млн. человек [6], Facebook же может похвастаться аудиторией более чем 1,5 млрд. человек. К тому же, наблюдается ежемесячный рост пользователей во всех наиболее известных социальных сетях.
В современном мире социальные сети являются мощным инструментом, который используется не только для общения, но и для распространения информации, рекламы, а также для наблюдения настроений в обществе. Социальные сети способны не только объединять людей, но и сделать лучших друзей врагами, если их мнения не сошлись в каком-либо вопросе. Человек, умеющий подать информацию, способен управлять если не толпой, то пользователями социальных сетей точно.
В описании социальных сетей и процессов, которые в них протекают, широкое распространение получили теория игр и теория графов.
Теория игр — раздел математики, основным предметом которого является поиск оптимальных стратегий в ситуациях, когда две или более сторон ведут борьбу за реализацию своих интересов. Такие ситуации называются играми. В каждой игре игроки следуют определенной стратегии, которая приведет каждого к проигрышу или выигрышу. При выборе стратегии каждому игроку необходимо опираться не только на максимизацию своего выигрыша, но и учитывать поведение другого игрока. Методам теории игр находят применение в экономике (наиболее частое применение), медицине, психологии, социологии, политологи, военном деле и т. д.
Теория графов — раздел дискретной математики, в которой изучаются свойства графов. В общем виде графом является набор из вершин (узлов), соединенных ребрами. Практическое применение теории графов достаточно широко, так как графы позволяют описывать не только технические процессы, но и многие другие: экономические, логистические, биологические и т. д.
Основные понятия иопределения
Основными понятиями в теории социальных сетей являются: агент, влияние, мнение, репутация. Приведем определения тех понятий, которые будут использоваться в нашем исследовании. Влияние — процесс и результат изменения субъектом поведения другого субъекта, его установок, намерений, представлений и оценок в ходе взаимодействия с ним [1]. Агент — участник (игрок) социальной сети.
Кооперативной игрой с трансферабельной полезностью называется пара ![]() , где
, где ![]() — множество игроков, а v — характеристическая функция (или функция выигрыша):
— множество игроков, а v — характеристическая функция (или функция выигрыша): ![]() ,
, ![]() Непустое множество S:
Непустое множество S: ![]() , называется коалицией. Характеристическая функция подчиняется следующим свойствам [4]:
, называется коалицией. Характеристическая функция подчиняется следующим свойствам [4]:
-
монотонность:
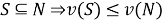 ;
;
-
супераддитивность:
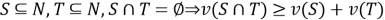 ;
;
-
выпуклость:
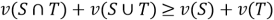 .
.
В теории кооперативных игр под характеристической функцией понимается отображение, ставящее в соответствие любой допустимой коалиции величину выигрыша, которая эта коалиция может получить, действуя независимо от остальных участников [4]. Смысл характеристической функции в данной работе будет состоять в том, что величина данной функции будет определять степень влияния агентов.
Вектор ![]() называется дележом. Именно дележ описывает исход игры. Каждая компонента вектора подчиняется следующим условиям:
называется дележом. Именно дележ описывает исход игры. Каждая компонента вектора подчиняется следующим условиям:
-
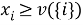 — условие индивидуальной рациональности;
— условие индивидуальной рациональности;
-
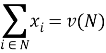 — условие коллективной рациональности.
— условие коллективной рациональности.
Вектор Шепли — принцип оптимальности распределения выигрыша между игроками в задачах кооперативной теории игр [4]. Является распределением, в котором выигрыш каждого игрока равен среднему вкладу игрока в общий выигрыш всей коалиции:
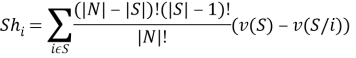 (1)
(1)
В рассматриваемой задаче вектор Шепли будет рассматриваться как оценка влияния одного агента на другого. Следовательно, по величине вектора Шепли можно будет определить то, какие игроки в социальной сети являются наиболее влиятельными.
Для применения теории графов необходимо ввести понятие ориентированного графа. Пусть задано конечное множество элементов X={1,2,3,…,n}, под которым будем понимать множество вершин, и подмножество V декартова произведения ![]() , то есть
, то есть ![]() , называемое множеством дуг, тогда ориентированным графом G является совокупность (X,V). Дугу между вершинами i и j будем обозначать как (i,j) [2].
, называемое множеством дуг, тогда ориентированным графом G является совокупность (X,V). Дугу между вершинами i и j будем обозначать как (i,j) [2].
Пример практического применения вектора Шепли взадаче оценки влияния всоциальных сетях
Как говорилось ранее, теория графов и теория игр получили широкое применение в исследовании социальных сетей, поэтому было введено понятие игр на социальных сетях. Игры на социальных сетях — игры, в которых вершинами являются агенты (игроки), а взвешенные дуги отображают степень доверия или влияния друг на друга [3].
Существует несколько классов наиболее часто используемых моделей для изучения процессов, протекающих в социальных сетях: оптимизационные и имитационные, теоретико-игровые, модели «диффузии инноваций». Рассмотрим модель взаимной информированности, которая принадлежит к классу теоретико-игровых моделей. В описании данной модели [3] было отмечено, что агенты сети не объединяются в коалиции и действуют каждый сам по себе, однако каждый агент знает о степени влияния других агентов. Также в [5] был описан подход, в котором определяется ценность агента. На основе данных методов рассмотрим ситуацию, когда агенты объединяются в коалиции, таким образом, имеет место коллективного влияния. Для этого, используем следующую социальную сеть, которая состоит из 4 агентов:
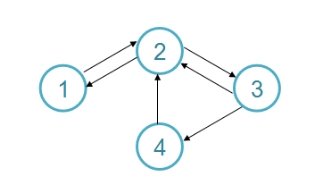
Рис. 1 Социальная сеть
Степень влияния агентов представлена следующими соотношениями:
![]()
![]()
Вычисляя вектор Шепли по формуле (1), получим следующие результаты:
![]() .
.
Данные результаты свидетельствуют о том, что наиболее влиятельными агентами в сети являются агенты под номерами 2 и 4, хотя агент номер 4 напрямую влияет только на игрока под номером 2. Следует заметить, что, несмотря на влияние агента под номером 3 на агентов 2 и 4, его ценность является наименьшей в данной игре. Полученный вектор оценок ценности удовлетворяет условиям рациональности, которые определены для вектора дележа.
В заключении хотелось бы сказать, что использование вектора Шепли для оценки значимости объединения игроков получило широкое распространение не только при решении социальных и экономических задач, но и, к примеру, в медицине (взаимодействие нейронов в головном мозге), и в генетике (измерение «силы генов»). В данной же статье была представлена идея применения вектора Шепли к оценке влиятельности агентов в социальных сетях.
Литература:
- Glossary on Control Theory and its Applications — http://glossary.ru
- Бурков В. Н., Заложнев А. Ю., Новиков Д. А. Теория графов в управлении организационными системами. М.: Синтег, 2001.-124с.
- Губанов Д. А., Новиков Д. А., Чхартишвили А. Г. Социальные сети: модели информационного влияния, управления и противоборства. М.:Физматлит, 2010.-228с.
- Петросян Л. А., Зенкевич Н. А., Шевкопляс Е. В. Теория игр. СПб: БХВ-Петербург, 2012.
- Чхартишвили А. Г. Теоретико-игровые модели информационного управления. М.: ЗАО «ПМСОФТ», 2004.- 227 с.
- http://br-analytics.ru/blog/socialnye-seti-v-rossii-zima-2015-2016-cifry-trendy-prognozy/







